Next: 2.2 : An Optimized Up: 2. Array-Based Lists Previous: 2. Array-Based Lists Contents Index
An
![]() implements the list interface using an array
implements the list interface using an array
![]() , called
the backing array. The list element with index
, called
the backing array. The list element with index
![]() is stored
in
is stored
in
![]() . At most times,
. At most times,
![]() is larger than strictly necessary,
so an integer
is larger than strictly necessary,
so an integer
![]() is used to keep track of the number of elements
actually stored in
is used to keep track of the number of elements
actually stored in
![]() . In this way, the list elements are stored in
. In this way, the list elements are stored in
![]() ,...,
,...,
![]() and, at all times,
and, at all times,
![]() .
.
array<T> a;
int n;
int size() {
return n;
}
Accessing and modifying the elements of an
![]() using
using
![]() and
and
![]() is trivial. After performing any necessary bounds-checking
we simply return or set, respectively,
is trivial. After performing any necessary bounds-checking
we simply return or set, respectively,
![]() .
.
T get(int i) {
return a[i];
}
T set(int i, T x) {
T y = a[i];
a[i] = x;
return y;
}
The operations of adding and removing elements from an
![]() are illustrated in Figure 2.1. To implement the
are illustrated in Figure 2.1. To implement the
![]() operation, we first check if
operation, we first check if
![]() is already full. If so, we call
the method
is already full. If so, we call
the method
![]() to increase the size of
to increase the size of
![]() . How
. How
![]() is implemented will be discussed later. For now, it is sufficient to
know that, after a call to
is implemented will be discussed later. For now, it is sufficient to
know that, after a call to
![]() , we can be sure that
, we can be sure that
![]() . With this out of the way, we now shift the elements
. With this out of the way, we now shift the elements
![]() right by one position to make room for
right by one position to make room for
![]() ,
set
,
set
![]() equal to
equal to
![]() , and increment
, and increment
![]() .
.
![\includegraphics[scale=0.90909]{figs/arraystack}](img633.png)
|
void add(int i, T x) {
if (n + 1 > a.length) resize();
for (int j = n; j > i; j--)
a[j] = a[j - 1];
a[i] = x;
n++;
}
If we ignore the cost of the potential call to
Implementing the
![]() operation is similar. We shift the elements
operation is similar. We shift the elements
![]() left by one position (overwriting
left by one position (overwriting
![]() ) and
decrease the value of
) and
decrease the value of
![]() . After doing this, we check if
. After doing this, we check if
![]() is getting
much smaller than
is getting
much smaller than
![]() by checking if
by checking if
![]() . If so,
then we call
. If so,
then we call
![]() to reduce the size of
to reduce the size of
![]() .
.
T remove(int i) {
T x = a[i];
for (int j = i; j < n - 1; j++)
a[j] = a[j + 1];
n--;
if (a.length >= 3 * n) resize();
return x;
}
If we ignore the cost of the
The
![]() method is fairly straightforward; it allocates a new
array
method is fairly straightforward; it allocates a new
array
![]() whose size is
whose size is
![]() and copies the
and copies the
![]() elements of
elements of
![]() into
the first
into
the first
![]() positions in
positions in
![]() , and then sets
, and then sets
![]() to
to
![]() . Thus, after a call to
. Thus, after a call to
![]() ,
,
![]() .
.
void resize() {
array<T> b(max(2 * n, 1));
for (int i = 0; i < n; i++)
b[i] = a[i];
a = b;
}
Analyzing the actual cost of the
![]() operation is easy. It
allocates an array
operation is easy. It
allocates an array
![]() of size
of size
![]() and copies the
and copies the
![]() elements of
elements of
![]() into
into
![]() . This takes
. This takes
![]() time.
time.
The running time analysis from the previous section ignored the cost
of calls to
![]() . In this section we analyze this cost using a
technique known as amortized analysis. This technique does not
try to determine the cost of resizing during each individual
. In this section we analyze this cost using a
technique known as amortized analysis. This technique does not
try to determine the cost of resizing during each individual
![]() and
and
![]() operation. Instead, it considers the cost of all calls to
operation. Instead, it considers the cost of all calls to
![]() during a sequence of
during a sequence of ![]() calls to
calls to
![]() or
or
![]() .
In particular, we will show:
.
In particular, we will show:
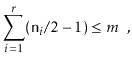
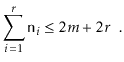
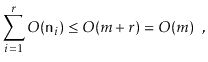
There are two cases to consider. In the first case,
![]() is
being called by
is
being called by
![]() because the backing array
because the backing array
![]() is full, i.e.,
is full, i.e.,
![]() . Consider the previous call to
. Consider the previous call to
![]() :
after this previous call, the size of
:
after this previous call, the size of
![]() was
was
![]() , but the
number of elements stored in
, but the
number of elements stored in
![]() was at most
was at most
![]() .
But now the number of elements stored in
.
But now the number of elements stored in
![]() is
is
![]() ,
so there must have been at least
,
so there must have been at least
![]() calls to
calls to
![]() since
the previous call to
since
the previous call to
![]() .
.
The second case occurs when
![]() is being called by
is being called by
![]() because
because
![]() . Again, after the
previous call to
. Again, after the
previous call to
![]() the number of elements stored in
the number of elements stored in
![]() was
at least
was
at least
![]() .2.1 Now there
are
.2.1 Now there
are
![]() elements stored in
elements stored in
![]() . Therefore, the number
of
. Therefore, the number
of
![]() operations since the last call to
operations since the last call to
![]() is at least
is at least
The following theorem summarizes the performance of an
![]() :
:
The
![]() is an efficient way to implement a
is an efficient way to implement a
![]() .
In particular, we can implement
.
In particular, we can implement
![]() as
as
![]() and
and
![]() as
as
![]() , in which case these operations will run in
, in which case these operations will run in ![]() amortized time.
amortized time.