Next: 9.4 Discussion and Exercises Up: 9. Red-Black Trees Previous: 9.2 RedBlackTree: A Simulated Contents Index
The following theorem summarizes the performance of the RedBlackTree data structure:
Not included in the above theorem is the following extra bonus:
We only sketch a proof of Theorem 9.2. By comparing
![]() and
and
![]() with the algorithms for adding or
removing a leaf in a 2-4 tree, we can convince ourselves that this
property is inherited from a 2-4 tree. In particular, if we can show
that the total time spent splitting, merging, and borrowing in a 2-4
tree is
with the algorithms for adding or
removing a leaf in a 2-4 tree, we can convince ourselves that this
property is inherited from a 2-4 tree. In particular, if we can show
that the total time spent splitting, merging, and borrowing in a 2-4
tree is ![]() , then this implies Theorem 9.2.
, then this implies Theorem 9.2.
The proof of this theorem for 2-4 trees uses the potential
method
of amortized analysis.9.2 Define the potential of an
internal node
![]() in a 2-4 tree as
in a 2-4 tree as
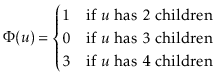
Next notice that, if we ignore splitting and merging of nodes, there are only a constant number of nodes whose number of children is changed by the addition or removal of a leaf. When adding a node, one node has its number of children increase by one, increasing the potential by at most three. During the removal of a leaf, one node has its number of children decrease by one, increasing the potential by at most one, and two nodes may be involved in a borrowing operation, increasing their total potential by at most one.
To summarize, each merge and split causes the potential to drop by
at least two. Ignoring merging and splitting, each addition or removal
causes the potential to rise by at most three, and the potential is always
non-negative. Therefore, the number of splits and merges caused by ![]() additions or removals on an initially empty tree is at most
additions or removals on an initially empty tree is at most ![]() .
Theorem 9.2 is a consequence of this analysis and the
correspondence between 2-4 trees and red-black trees.
.
Theorem 9.2 is a consequence of this analysis and the
correspondence between 2-4 trees and red-black trees.