Next: 9.3 Summary Up: 9. Red-Black Trees Previous: 9.1 2-4 Trees Contents Index
A red-black tree is a binary search tree in which each node,
![]() ,
has a colour
which is either red or black. Red is
represented by the value 0 and black by the value
,
has a colour
which is either red or black. Red is
represented by the value 0 and black by the value ![]() .
.
Before and after any operation on a red-black tree, the following two properties are satisfied. Each property is defined both in terms of the colours red and black, and in terms of the numeric values 0 and 1.
Notice that we can always colour the root,
![\includegraphics[scale=0.90909]{figs-python/24rb-1}](img3542.png)
|
At first it might seem surprising that a red-black tree can be efficiently updated to maintain the black-height and no-red-edge properties, and it seems unusual to even consider these as useful properties. However, red-black trees were designed to be an efficient simulation of 2-4 trees as binary trees.
Refer to Figure 9.5.
Consider any red-black tree, ![]() , having
, having
![]() nodes and perform the
following transformation: Remove each red node
nodes and perform the
following transformation: Remove each red node
![]() and connect
and connect
![]() 's two
children directly to the (black) parent of
's two
children directly to the (black) parent of
![]() . After this transformation
we are left with a tree
. After this transformation
we are left with a tree ![]() having only black nodes.
having only black nodes.
Every internal node in ![]() has two, three, or four children: A black
node that started out with two black children will still have two
black children after this transformation. A black node that started
out with one red and one black child will have three children after this
transformation. A black node that started out with two red children will
have four children after this transformation. Furthermore, the black-height
property now guarantees that every root-to-leaf path in
has two, three, or four children: A black
node that started out with two black children will still have two
black children after this transformation. A black node that started
out with one red and one black child will have three children after this
transformation. A black node that started out with two red children will
have four children after this transformation. Furthermore, the black-height
property now guarantees that every root-to-leaf path in ![]() has the
same length. In other words,
has the
same length. In other words, ![]() is a 2-4 tree!
is a 2-4 tree!
The 2-4 tree ![]() has
has
![]() leaves that correspond to the
leaves that correspond to the
![]() external nodes of the red-black tree. Therefore, this tree has height
at most
external nodes of the red-black tree. Therefore, this tree has height
at most
![]() . Now, every root to leaf path in the 2-4 tree corresponds
to a path from the root of the red-black tree
. Now, every root to leaf path in the 2-4 tree corresponds
to a path from the root of the red-black tree ![]() to an external node.
The first and last node in this path are black and at most one out of
every two internal nodes is red, so this path has at most
to an external node.
The first and last node in this path are black and at most one out of
every two internal nodes is red, so this path has at most
![]() black nodes and at most
black nodes and at most
![]() red nodes. Therefore, the longest path from the root to any internal node in
red nodes. Therefore, the longest path from the root to any internal node in ![]() is at most
is at most
Now that we have seen the relationship between 2-4 trees and red-black trees, it is not hard to believe that we can efficiently maintain a red-black tree while adding and removing elements.
We have already seen that adding an element in a BinarySearchTree
can be done by adding a new leaf. Therefore, to implement
![]() in a
red-black tree we need a method of simulating splitting a node with five
children in a 2-4 tree. A 2-4 tree node with five children is represented
by a black node that has two red children, one of which also has a red
child. We can ``split'' this node by colouring it red and colouring its
two children black. An example of this is shown in Figure 9.6.
in a
red-black tree we need a method of simulating splitting a node with five
children in a 2-4 tree. A 2-4 tree node with five children is represented
by a black node that has two red children, one of which also has a red
child. We can ``split'' this node by colouring it red and colouring its
two children black. An example of this is shown in Figure 9.6.
|
Similarly, implementing
![]() requires a method of merging two nodes
and borrowing a child from a sibling. Merging two nodes is the inverse of
a split (shown in Figure 9.6), and involves colouring two (black)
siblings red and colouring their (red) parent black. Borrowing from
a sibling is the most complicated of the procedures and involves both
rotations and recolouring nodes.
requires a method of merging two nodes
and borrowing a child from a sibling. Merging two nodes is the inverse of
a split (shown in Figure 9.6), and involves colouring two (black)
siblings red and colouring their (red) parent black. Borrowing from
a sibling is the most complicated of the procedures and involves both
rotations and recolouring nodes.
Of course, during all of this we must still maintain the no-red-edge property and the black-height property. While it is no longer surprising that this can be done, there are a large number of cases that have to be considered if we try to do a direct simulation of a 2-4 tree by a red-black tree. At some point, it just becomes simpler to disregard the underlying 2-4 tree and work directly towards maintaining the properties of the red-black tree.
No single definition of red-black trees exists. Rather, there is
a family of structures that manage to maintain the black-height
and no-red-edge properties during
![]() and
and
![]() operations. Different structures do this in different ways.
Here, we implement a data structure that we call a RedBlackTree.
This structure implements a particular variant of red-black trees that
satisfies an additional property:
operations. Different structures do this in different ways.
Here, we implement a data structure that we call a RedBlackTree.
This structure implements a particular variant of red-black trees that
satisfies an additional property:
Note that the red-black tree shown in Figure 9.4 does not satisfy the left-leaning property; it is violated by the parent of the red node in the rightmost path.
The reason for maintaining the left-leaning property is that it reduces
the number of cases encountered when updating the tree during
![]() and
and
![]() operations. In terms of 2-4 trees, it implies that every
2-4 tree has a unique representation: A node of degree two becomes
a black node with two black children. A node of degree three becomes
a black node whose left child is red and whose right child is black.
A node of degree four becomes a black node with two red children.
operations. In terms of 2-4 trees, it implies that every
2-4 tree has a unique representation: A node of degree two becomes
a black node with two black children. A node of degree three becomes
a black node whose left child is red and whose right child is black.
A node of degree four becomes a black node with two red children.
Before we describe the implementation of
![]() and
and
![]() in
detail, we first present some simple subroutines used by these methods
that are illustrated in Figure 9.7. The first two
subroutines are for manipulating colours while preserving the black-height
property. The
in
detail, we first present some simple subroutines used by these methods
that are illustrated in Figure 9.7. The first two
subroutines are for manipulating colours while preserving the black-height
property. The
![]() method takes as input a black node
method takes as input a black node
![]() that has two red children and colours
that has two red children and colours
![]() red and its two children black.
The
red and its two children black.
The
![]() method reverses this operation:
method reverses this operation:

The
![]() method swaps the colours of
method swaps the colours of
![]() and
and
![]() and then performs a left rotation at
and then performs a left rotation at
![]() . This method reverses the
colours of these two nodes as well as their parent-child relationship:
. This method reverses the
colours of these two nodes as well as their parent-child relationship:
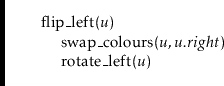
The
![]() operation
is especially useful in restoring the left-leaning property at a node
operation
is especially useful in restoring the left-leaning property at a node
![]() that violates it (because
that violates it (because
![]() is black and
is black and
![]() is red).
In this special case, we can be assured that this operation preserves both
the black-height and no-red-edge properties. The
is red).
In this special case, we can be assured that this operation preserves both
the black-height and no-red-edge properties. The
![]() operation
is symmetric with
operation
is symmetric with
![]() , when the roles of left and right are reversed.
, when the roles of left and right are reversed.
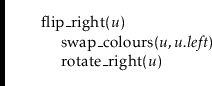
To implement
![]() in a RedBlackTree, we perform a standard
BinarySearchTree insertion to add a new leaf,
in a RedBlackTree, we perform a standard
BinarySearchTree insertion to add a new leaf,
![]() , with
, with
![]() and
set
and
set
![]() . Note that this does not change the black height
of any node, so it does not violate the black-height property. It may,
however, violate the left-leaning property (if
. Note that this does not change the black height
of any node, so it does not violate the black-height property. It may,
however, violate the left-leaning property (if
![]() is the right child of
its parent), and it may violate the no-red-edge property (if
is the right child of
its parent), and it may violate the no-red-edge property (if
![]() 's parent
is
's parent
is
![]() ). To restore these properties, we call the method
). To restore these properties, we call the method
![]() .
.

Illustrated in Figure 9.8, the
![]() method takes
as input a node
method takes
as input a node
![]() whose colour is red and which may violate the
no-red-edge property and/or the left-leaning property. The following
discussion is probably impossible to follow without referring to
Figure 9.8 or recreating it on a piece of paper. Indeed, the
reader may wish to study this figure before continuing.
whose colour is red and which may violate the
no-red-edge property and/or the left-leaning property. The following
discussion is probably impossible to follow without referring to
Figure 9.8 or recreating it on a piece of paper. Indeed, the
reader may wish to study this figure before continuing.
If
![]() is the root of the tree, then we can colour
is the root of the tree, then we can colour
![]() black to restore
both properties. If
black to restore
both properties. If
![]() 's sibling is also red, then
's sibling is also red, then
![]() 's parent must be
black, so both the left-leaning and no-red-edge properties already hold.
's parent must be
black, so both the left-leaning and no-red-edge properties already hold.
Otherwise, we first determine if
![]() 's parent,
's parent,
![]() , violates the
left-leaning property and, if so, perform a
, violates the
left-leaning property and, if so, perform a
![]() operation and
set
operation and
set
![]() . This leaves us in a well-defined state:
. This leaves us in a well-defined state:
![]() is the left
child of its parent,
is the left
child of its parent,
![]() , so
, so
![]() now satisfies the left-leaning property.
All that remains is to ensure the no-red-edge property at
now satisfies the left-leaning property.
All that remains is to ensure the no-red-edge property at
![]() . We only
have to worry about the case in which
. We only
have to worry about the case in which
![]() is red, since otherwise
is red, since otherwise
![]() already satisfies the no-red-edge property.
already satisfies the no-red-edge property.
Since we are not done yet,
![]() is red and
is red and
![]() is red. The no-red-edge
property (which is only violated by
is red. The no-red-edge
property (which is only violated by
![]() and not by
and not by
![]() ) implies that
) implies that
![]() 's grandparent
's grandparent
![]() exists and is black. If
exists and is black. If
![]() 's right child is red,
then the left-leaning property ensures that both
's right child is red,
then the left-leaning property ensures that both
![]() 's children are red,
and a call to
's children are red,
and a call to
![]() makes
makes
![]() red and
red and
![]() black. This restores
the no-red-edge property at
black. This restores
the no-red-edge property at
![]() , but may cause it to be violated at
, but may cause it to be violated at
![]() ,
so the whole process starts over with
,
so the whole process starts over with
![]() .
.
If
![]() 's right child is black, then a call to
's right child is black, then a call to
![]() makes
makes
![]() the (black) parent of
the (black) parent of
![]() and gives
and gives
![]() two red children,
two red children,
![]() and
and
![]() . This ensures that
. This ensures that
![]() satisfies the no-red-edge property and
satisfies the no-red-edge property and
![]() satisfies the left-leaning property. In this case we can stop.
satisfies the left-leaning property. In this case we can stop.

The
![]() method takes constant time per iteration and each
iteration either finishes or moves
method takes constant time per iteration and each
iteration either finishes or moves
![]() closer to the root. Therefore,
the
closer to the root. Therefore,
the
![]() method finishes after
method finishes after
![]() iterations in
iterations in
![]() time.
time.
The
![]() operation in a RedBlackTree is the most complicated
to implement, and this is true of all known red-black tree variants.
Just like the
operation in a RedBlackTree is the most complicated
to implement, and this is true of all known red-black tree variants.
Just like the
![]() operation in a BinarySearchTree,
this operation boils down to finding a node
operation in a BinarySearchTree,
this operation boils down to finding a node
![]() with only one child,
with only one child,
![]() , and splicing
, and splicing
![]() out of the tree by having
out of the tree by having
![]() adopt
adopt
![]() .
.
The problem with this is that, if
![]() is black, then the black-height
property will now be violated at
is black, then the black-height
property will now be violated at
![]() . We may avoid this problem,
temporarily, by adding
. We may avoid this problem,
temporarily, by adding
![]() to
to
![]() . Of course, this introduces
two other problems: (1) if
. Of course, this introduces
two other problems: (1) if
![]() and
and
![]() both started out black, then
both started out black, then
![]() (double black), which is an invalid colour.
If
(double black), which is an invalid colour.
If
![]() was red, then it is replaced by a black node
was red, then it is replaced by a black node
![]() , which may
violate the left-leaning property at
, which may
violate the left-leaning property at
![]() . Both of these
problems can be resolved with a call to the
. Both of these
problems can be resolved with a call to the
![]() method.
method.
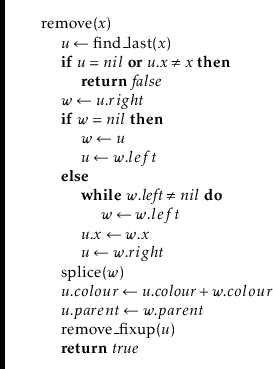
The
![]() method takes as its input a node
method takes as its input a node
![]() whose colour is black
(1) or double-black (2). If
whose colour is black
(1) or double-black (2). If
![]() is double-black, then
is double-black, then
![]() performs a series of rotations and recolouring operations that move the
double-black node up the tree until it can be eliminated. During this
process, the node
performs a series of rotations and recolouring operations that move the
double-black node up the tree until it can be eliminated. During this
process, the node
![]() changes until, at the end of this process,
changes until, at the end of this process,
![]() refers to the root of the subtree that has been changed. The root of
this subtree may have changed colour. In particular, it may have gone
from red to black, so the
refers to the root of the subtree that has been changed. The root of
this subtree may have changed colour. In particular, it may have gone
from red to black, so the
![]() method finishes by checking
if
method finishes by checking
if
![]() 's parent violates the left-leaning property and, if so, fixing it.
's parent violates the left-leaning property and, if so, fixing it.

The
![]() method is illustrated in Figure 9.9.
Again, the following text will be difficult, if not impossible, to follow
without referring to Figure 9.9. Each iteration of the loop
in
method is illustrated in Figure 9.9.
Again, the following text will be difficult, if not impossible, to follow
without referring to Figure 9.9. Each iteration of the loop
in
![]() processes the double-black node
processes the double-black node
![]() , based on one
of four cases:
, based on one
of four cases:
Case 0:
![]() is the root. This is the easiest case to treat. We recolour
is the root. This is the easiest case to treat. We recolour
![]() to be black (this does not violate any of the red-black tree
properties).
to be black (this does not violate any of the red-black tree
properties).
Case 1:
![]() 's sibling,
's sibling,
![]() , is red. In this case,
, is red. In this case,
![]() 's sibling is the
left child of its parent,
's sibling is the
left child of its parent,
![]() (by the left-leaning property). We perform
a right-flip at
(by the left-leaning property). We perform
a right-flip at
![]() and then proceed to the next iteration. Note that
this action causes
and then proceed to the next iteration. Note that
this action causes
![]() 's parent to violate the left-leaning property and
the depth of
's parent to violate the left-leaning property and
the depth of
![]() to increase. However, it also implies that the next
iteration will be in Case 3 with
to increase. However, it also implies that the next
iteration will be in Case 3 with
![]() coloured red. When examining Case 3
below, we will see that the process will stop during the next iteration.
coloured red. When examining Case 3
below, we will see that the process will stop during the next iteration.
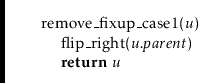
Case 2:
![]() 's sibling,
's sibling,
![]() , is black, and
, is black, and
![]() is the left child of its
parent,
is the left child of its
parent,
![]() . In this case, we call
. In this case, we call
![]() , making
, making
![]() black,
black,
![]() red, and darkening the colour of
red, and darkening the colour of
![]() to black or double-black.
At this point,
to black or double-black.
At this point,
![]() does not satisfy the left-leaning property, so we
call
does not satisfy the left-leaning property, so we
call
![]() to fix this.
to fix this.
At this point,
![]() is red and
is red and
![]() is the root of the subtree with which
we started. We need to check if
is the root of the subtree with which
we started. We need to check if
![]() causes the no-red-edge property to
be violated. We do this by inspecting
causes the no-red-edge property to
be violated. We do this by inspecting
![]() 's right child,
's right child,
![]() . If
. If
![]() is black, then
is black, then
![]() satisfies the no-red-edge property and we can continue
the next iteration with
satisfies the no-red-edge property and we can continue
the next iteration with
![]() .
.
Otherwise (
![]() is red), so both the no-red-edge property and the left-leaning
properties are violated at
is red), so both the no-red-edge property and the left-leaning
properties are violated at
![]() and
and
![]() , respectively. The left-leaning
property is restored with a call to
, respectively. The left-leaning
property is restored with a call to
![]() , but the no-red-edge
property is still violated. At this point,
, but the no-red-edge
property is still violated. At this point,
![]() is the left child of
is the left child of
![]() ,
,
![]() is the left child of
is the left child of
![]() ,
,
![]() and
and
![]() are both red, and
are both red, and
![]() is black or double-black. A
is black or double-black. A
![]() makes
makes
![]() the parent of
both
the parent of
both
![]() and
and
![]() . Following this up by a
. Following this up by a
![]() makes both
makes both
![]() and
and
![]() black and sets the colour of
black and sets the colour of
![]() back to the original colour of
back to the original colour of
![]() .
.
At this point, the double-black node is has been eliminated and the
no-red-edge and black-height properties are reestablished. Only one possible problem remains: the right child of
![]() may be red, in which
case the left-leaning property would be violated. We check this and
perform a
may be red, in which
case the left-leaning property would be violated. We check this and
perform a
![]() to correct it if necessary.
to correct it if necessary.

Case 3:
![]() 's sibling is black and
's sibling is black and
![]() is the right child of its parent,
is the right child of its parent,
![]() . This case is symmetric to Case 2 and is handled mostly the same way.
The only differences come from the fact that the left-leaning property
is asymmetric, so it requires different handling.
. This case is symmetric to Case 2 and is handled mostly the same way.
The only differences come from the fact that the left-leaning property
is asymmetric, so it requires different handling.
As before, we begin with a call to
![]() , which makes
, which makes
![]() red
and
red
and
![]() black. A call to
black. A call to
![]() promotes
promotes
![]() to the root of
the subtree. At this point
to the root of
the subtree. At this point
![]() is red, and the code branches two ways
depending on the colour of
is red, and the code branches two ways
depending on the colour of
![]() 's left child,
's left child,
![]() .
.
If
![]() is red, then the code finishes up exactly the same way as Case 2
does, but is even simpler since there is no danger of
is red, then the code finishes up exactly the same way as Case 2
does, but is even simpler since there is no danger of
![]() not
satisfying the left-leaning property.
not
satisfying the left-leaning property.
The more complicated case occurs when
![]() is black. In this case,
we examine the colour of
is black. In this case,
we examine the colour of
![]() 's left child. If it is red, then
's left child. If it is red, then
![]() has
two red children and its extra black can be pushed down with a call to
has
two red children and its extra black can be pushed down with a call to
![]() . At this point,
. At this point,
![]() now has
now has
![]() 's original colour, and we
are done.
's original colour, and we
are done.
If
![]() 's left child is black, then
's left child is black, then
![]() violates the left-leaning property,
and we restore this with a call to
violates the left-leaning property,
and we restore this with a call to
![]() . We then return the
node
. We then return the
node
![]() so that the next iteration of
so that the next iteration of
![]() then continues
with
then continues
with
![]() .
.

Each iteration of
![]() takes constant time. Cases 2 and 3
either finish or move
takes constant time. Cases 2 and 3
either finish or move
![]() closer to the root of the tree. Case 0 (where
closer to the root of the tree. Case 0 (where
![]() is the root) always terminates and Case 1 leads immediately to Case 3,
which also terminates. Since the height of the tree is at most
is the root) always terminates and Case 1 leads immediately to Case 3,
which also terminates. Since the height of the tree is at most
![]() , we conclude that there are at most
, we conclude that there are at most
![]() iterations of
iterations of
![]() , so
, so
![]() runs in
runs in
![]() time.
time.
opendatastructures.org