Next: 5.4 Discussion and Exercises Up: 5. Hash Tables Previous: 5.2 : Linear Probing Contents Index
The hash tables discussed in the previous section are used to associate
data with integer keys consisting of
bits. In many cases, we
have keys that are not integers. They may be strings, objects, arrays,
or other compound structures. To use hash tables for these types of data,
we must map these data types to
-bit hash codes. Hash code mappings should
have the following properties:
and
are equal, then
and
are equal.
and
are not equal, then the probability that
should be small (close to
).
The first property ensures that if we store
in a hash table and later
look up a value
equal to
, then we will find
--as we should.
The second property minimizes the loss from converting our objects
to integers. It ensures that unequal objects usually have different
hash codes and so are likely to be stored at different locations in
our hash table.
Small primitive data types like
,
,
, and
are
usually easy to find hash codes for. These data types always have a
binary representation and this binary representation usually consists of
or fewer bits. (For example, in C++
is typically an 8-bit type and
is a 32-bit type.) In these
cases, we just treat these bits as the representation of an integer in
the range
. If two values are different, they get
different hash codes. If they are the same, they get the same hash code.
A few primitive data types are made up of more than
bits, usually
bits for some constant integer 
. (Java's
and
types are examples of this with 
.) These data types can be treated
as compound objects made of 
parts, as described in the next section.
For a compound object, we want to create a hash code by combining the
individual hash codes of the object's constituent parts. This is not
as easy as it sounds. Although one can find many hacks for this (for
example, combining the hash codes with bitwise exclusive-or operations),
many of these hacks turn out to be easy to foil (see Exercises 5.7-5.9).
However, if one is willing to do arithmetic with
bits of
precision, then there are simple and robust methods available.
Suppose we have an object made up of several parts
whose hash codes are
.
Then we can choose mutually independent random
-bit integers
and a random
-bit odd integer
and
compute a hash code for our object with
and
dividing by
) that uses the multiplicative hash function
from Section 5.1.1 to take the
-bit intermediate result and
reduce it to a
-bit final result. Here is an example of this method applied to a simple compound object with three parts
,
, and
:
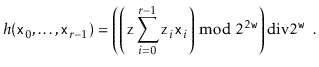
unsigned hashCode() {
// random number from random.org
long long z[] = {0x2058cc50L, 0xcb19137eL, 0x2cb6b6fdL};
long zz = 0xbea0107e5067d19dL;
long h0 = ods::hashCode(x0);
long h1 = ods::hashCode(x1);
long h2 = ods::hashCode(x2);
return (int)(((z[0]*h0 + z[1]*h1 + z[2]*h2)*zz) >> 32);
}
The following theorem shows that, in addition to being straightforward to implement, this method is provably good:
.
We can rewrite this as:
, then
(5.4) becomes
and
is at most
, so
their product is at most
.
By assumption,
, so (5.5) has at most one
solution in
. Therefore, since
and 
are
independent (
are mutually independent), the
probability that we select
so that
is at most
.
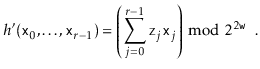
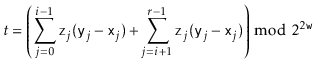
The final step of the hash function is to apply multiplicative hashing
to reduce our
-bit intermediate result
to
a
-bit final result
. By Theorem 5.3,
if
, then
.
To summarize,
 |
||
 |
||
 |
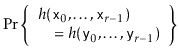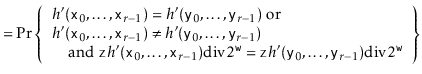The method from the previous section works well for objects that have a
fixed, constant, number of components. However, it breaks down when we
want to use it with objects that have a variable number of components,
since it requires a random
-bit integer
for each component.
We could use a pseudorandom sequence to generate as many
's as we
need, but then the
's are not mutually independent, and it becomes
difficult to prove that the pseudorandom numbers don't interact badly
with the hash function we are using. In particular, the values of 
and
in the proof of Theorem 5.3 are no longer independent.
A more rigorous approach is to base our hash codes on polynomials over
prime fields; these are just regular polynomials that are evaluated
modulo some prime number,
. This method is based on the following
theorem, which says that polynomials over prime fields behave pretty-much
like usual polynomials:
be a prime number, and let
be a non-trivial polynomial with coefficients
. Then the equation
has at most 
solutions for
.
To use Theorem 5.4, we hash a sequence of integers
with each
using
a random integer
via the formula
Note the extra
term at the end of the formula. It helps
to think of
as the last element,
, in the sequence
. Note that this element differs from every other
element in the sequence (each of which is in the set
).
We can think of
as an end-of-sequence marker.
The following theorem, which considers the case of two sequences of
the same length, shows that this hash function gives a good return for
the small amount of randomization needed to choose
:
be a prime, let
and
each be sequences of
-bit integers in
, and assume
for at least
one index
. Then
can be rewritten as
, this polynomial is non-trivial. Therefore,
by Theorem 5.4, it has at most 
solutions in
.
The probability that we pick
to be one of these solutions is therefore
at most
.
Note that this hash function also deals with the case in which two sequences have different lengths, even when one of the sequences is a prefix of the other. This is because this function effectively hashes the infinite sequence
and 
with 
, then these two sequences differ at index 
. In
this case, (5.6) becomes
solutions in
.
This combined with Theorem 5.5 suffice to prove the
following more general theorem:
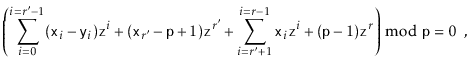
The following example code shows how this hash function is applied to
an object that contains an array,
, of values:
unsigned hashCode() {
long p = (1L<<32)-5; // prime: 2^32 - 5
long z = 0x64b6055aL; // 32 bits from random.org
int z2 = 0x5067d19d; // random odd 32 bit number
long s = 0;
long zi = 1;
for (int i = 0; i < x.length; i++) {
// reduce to 31 bits
long long xi = (ods::hashCode(x[i]) * z2) >> 1;
s = (s + zi * xi) % p;
zi = (zi * z) % p;
}
s = (s + zi * (p-1)) % p;
return (int)s;
}
The preceding code sacrifices some collision probability for implementation
convenience. In particular, it applies the multiplicative hash function
from Section 5.1.1, with
to reduce
![$ \mathtt{x[i].hashCode()}$](img3011.png){kind=small}
to a
31-bit value. This is so that the additions and multiplications that are
done modulo the prime
can be carried out using unsigned
63-bit arithmetic. Thus the probability of two different sequences,
the longer of which has length 
, having the same hash code is at most
specified in Theorem 5.6.
opendatastructures.org