Next: 5.2 : Linear Probing Up: 5. Hash Tables Previous: 5. Hash Tables Contents Index
: Hashing with Chaining
A
data structure uses hashing with chaining to store
data as an array,
, of lists. An integer,
, keeps track of the
total number of items in all lists (see Figure 5.1):
array<List> t; int n;The hash value of a data item
, denoted
is a value
in the range
. All items with hash value
are stored in the list at
![$ \mathtt{t[i]}$](img2423.png){kind=small}
. To ensure that lists don't get too
long, we maintain the invariant
.
To add an element,
, to the hash table, we first check if
the length of
needs to be increased and, if so, we grow
.
With this out of the way we hash
to get an integer,
, in the
range
, and we append
to the list
![$ \mathtt{t[i]}$](img2433.png){kind=small}
:
![\includegraphics[width=\textwidth ]{figs/chainedhashtable}](img2413.png)
bool add(T x) {
if (find(x) != null) return false;
if (n+1 > t.length) resize();
t[hash(x)].add(x);
n++;
return true;
}
Growing the table,
if necessary, involves doubling the length of
and reinserting
all elements into the new table. This strategy is exactly the same
as the one used in the implementation of
and the same
result applies: The cost of growing is only constant when amortized
over a sequence of insertions (see Lemma 2.1 on
page ![[*]](crossref.png)
).
Besides growing, the only other work done when adding a new value
to a
involves appending
to the list
![$ \mathtt{t[hash(x)]}$](img2439.png){kind=small}
. For
any of the list implementations described in Chapters 2
or 3, this takes only constant time.
To remove an element,
, from the hash table, we iterate over the list
![$ \mathtt{t[hash(x)]}$](img2441.png){kind=small}
until we find
so that we can remove it:
T remove(T x) {
int j = hash(x);
for (int i = 0; i < t[j].size(); i++) {
T y = t[j].get(i);
if (x == y) {
t[j].remove(i);
n--;
return y;
}
}
return null;
}
This takes
time, where
denotes the length
of the list stored at
![$ \mathtt{t[i]}$](img2445.png){kind=small}
.
Searching for the element
in a hash table is similar. We perform
a linear search on the list
![$ \mathtt{t[hash(x)]}$](img2447.png){kind=small}
:
T find(T x) {
int j = hash(x);
for (int i = 0; i < t[j].size(); i++)
if (x == t[j].get(i))
return t[j].get(i);
return null;
}
Again, this takes time proportional to the length of the list
![$ \mathtt{t[hash(x)]}$](img2448.png){kind=small}
.
The performance of a hash table depends critically on the choice of the
hash function. A good hash function will spread the elements evenly
among the
lists, so that the expected size of the list
![$ \mathtt{t[hash(x)]}$](img2450.png){kind=small}
is
. On the other hand, a bad
hash function will hash all values (including
) to the same table
location, in which case the size of the list
![$ \mathtt{t[hash(x)]}$](img2453.png){kind=small}
will be
.
In the next section we describe a good hash function.
Multiplicative hashing is an efficient method of generating hash
values based on modular arithmetic (discussed in Section 2.3)
and integer division. It uses the 
operator, which calculates
the integral part of a quotient, while discarding the remainder.
Formally, for any integers 
and 
,
.
In multiplicative hashing, we use a hash table of size
for some
integer
(called the dimension). The formula for hashing an
integer
is
is a randomly chosen odd integer in
. This hash function can be realized very
efficiently by observing that, by default, operations on integers
are already done modulo
where
is the number of bits
in an integer.5.1 (See
Figure 5.2.) Furthermore, integer division by
is equivalent to dropping the rightmost
bits in a binary
representation (which is implemented by shifting the bits right by
using the
operator). In this way, the code that implements the above
formula is simpler than the formula itself:
int hash(T x) {
return ((unsigned)(z * hashCode(x))) >> (w-d);
}
The following lemma, whose proof is deferred until later in this section, shows that multiplicative hashing does a good job of avoiding collisions:
With Lemma 5.1, the performance of
, and
are easy to analyze:
, the expected length of the list
![$ \mathtt{t[hash(x)]}$](img2485.png){kind=small}
is at most
, where
is the number of
occurrences of
in the hash table.
be the (multi-)set of elements stored in the hash table that
are not equal to
. For an element
, define the indicator
variable
![$ \mathrm{E}[I_{\ensuremath{\mathtt{y}}}] \le
2/2^{\ensuremath{\mathtt{d}}}=2/\ensuremath{\mathtt{t.length}}$](img2494.png){kind=small}
. The expected length of the list
![$ \mathtt{t[hash(x)]}$](img2495.png){kind=small}
is given by
![$\displaystyle \mathrm{E}\left[\ensuremath{\mathtt{t[hash(x)].size()}}\right]$](img2496.png){kind=small} |
 |
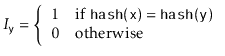
![$\displaystyle \mathrm{E}\left[\ensuremath{\mathtt{n}}_{\ensuremath{\mathtt{x}}} + \sum_{\ensuremath{\mathtt{y}}\in S} I_{\ensuremath{\mathtt{y}}}\right]$](img2498.png) |
|
 |
![$\displaystyle \ensuremath{\mathtt{n}}_{\ensuremath{\mathtt{x}}} + \sum_{\ensuremath{\mathtt{y}}\in S} \mathrm{E}[I_{\ensuremath{\mathtt{y}}} ]$](img2500.png) |
||
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |
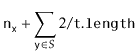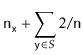Now, we want to prove Lemma 5.1, but first we need a
result from number theory. In the following proof, we use the notation
to denote
, where each 
is a bit, either 0 or 1. In other words,
is
the integer whose binary representation is given by
.
We use 
to denote a bit of unknown value.
be the set of odd integers in
; let 
and 
be any two elements in 
. Then there is exactly one value
such that
.
and 
is the same, it is
sufficient to prove that there is at most one value
that
satisfies
.
Suppose, for the sake of contradiction, that there are two such values
and
, with
. Then
. Thinking in terms of binary numbers, we have
trailing bits in the binary representation of
are all 0's.
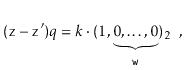
Furthermore 
, since 
and
. Since 
is odd, it has no trailing 0's in its binary representation:
,
has fewer than
trailing
0's in its binary representation:
has fewer than
trailing 0's in
its binary representation:
cannot satisfy (5.1), yielding a
contradiction and completing the proof.
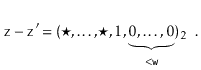
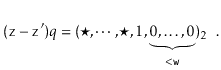
The utility of Lemma 5.3 comes from the following
observation: If
is chosen uniformly at random from 
, then
is uniformly distributed over 
. In the following proof, it helps
to think of the binary representation of
, which consists of
random bits followed by a 1.
is equivalent to
the statement ``the highest-order
bits of
and the highest-order
bits of
are the same.''
A necessary condition of that statement is that the highest-order
bits in the binary representation of
are either all 0's or all 1's. That is,
or
.
Therefore, we only have to bound the probability that
looks like (5.2) or (5.3).
Let 
be the unique odd integer such that
for some integer 
. By
Lemma 5.3, the binary representation of
has
random bits, followed by a 1:
has
random bits, followed by a 1, followed by 
0's:
, then the
higher order bits of
contain both 0's
and 1's, so the probability that
looks
like (5.2) or (5.3) is 0. If
,
then the probability of looking like (5.2) is 0, but the
probability of looking like (5.3) is
(since we must have
). If
,
then we must have
or
. The probability of each
of these cases is
and they are mutually exclusive, so the
probability of either of these cases is
. This completes
the proof.
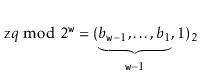
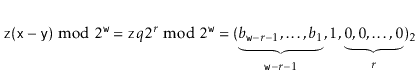
The following theorem summarizes the performance of a
data structure:
implements the
interface. Ignoring the cost of
calls to
, a
supports the operations
,
, and
in 
expected time per operation.
Furthermore, beginning with an empty
, any sequence of
and
operations results in a total of 
time spent during all calls to
.
-bit integer operation
that overflows is upgraded to a variable-length representation.
