Next: 6. Binary Trees Up: 5. Hash Tables Previous: 5.3 Hash Codes Contents Index
Hash tables and hash codes represent an enormous and active field of research that is just touched upon in this chapter. The online Bibliography on Hashing [10] contains nearly 2000 entries.
A variety of different hash table implementations exist. The one
described in Section 5.1 is known as hashing with chaining
(each array entry contains a chain (
) of elements). Hashing with
chaining dates back to an internal IBM memorandum authored by H. P. Luhn
and dated January 1953. This memorandum also seems to be one of the
earliest references to linked lists.
An alternative to hashing with chaining is that used by open
addressing schemes, where all data is stored directly in an
array. These schemes include the
structure of
Section 5.2. This idea was also proposed, independently, by
a group at IBM in the 1950s. Open addressing schemes must deal with the
problem of collision resolution:
the case where two values hash
to the same array location. Different strategies exist for collision
resolution; these provide different performance guarantees and often
require more sophisticated hash functions than the ones described here.
Yet another category of hash table implementations are the so-called
perfect hashing methods.
These are methods in which
operations take 
time in the worst-case. For static data sets,
this can be accomplished by finding perfect hash functions
for
the data; these are functions that map each piece of data to a unique
array location. For data that changes over time, perfect hashing
methods include FKS two-level hash tables
[31,24]
and cuckoo hashing [55].
The hash functions presented in this chapter are probably among the most
practical methods currently known that can be proven to work well for any
set of data. Other provably good methods date back to the pioneering work
of Carter and Wegman who introduced the notion of universal hashing
and described several hash functions for different scenarios [14].
Tabulation hashing, described in Section 5.2.3, is due to Carter
and Wegman [14], but its analysis, when applied to linear probing
(and several other hash table schemes) is due to P
tra
cu and
Thorup [58].
The idea of multiplicative hashing
is very old and seems to be
part of the hashing folklore [48, Section 6.4]. However, the
idea of choosing the multiplier
to be a random odd number,
and the analysis in Section 5.1.1 is due to Dietzfelbinger et al. [23]. This version of multiplicative hashing is one of the
simplest, but its collision probability of
is a factor of two
larger than what one could expect with a random function from
. The multiply-add hashing
method uses the function
and
are each randomly chosen from
.
Multiply-add hashing has a collision probability of only
[21], but requires
-bit precision arithmetic.
There are a number of methods of obtaining hash codes from fixed-length
sequences of
-bit integers. One particularly fast method
[11] is the function
is even and
are randomly chosen from
. This yields a
-bit hash code that has
collision probability
. This can be reduced to a
-bit hash
code using multiplicative (or multiply-add) hashing. This method is fast
because it requires only 
-bit multiplications whereas the
method described in Section 5.3.2 requires 
multiplications.
(The 
operations occur implicitly by using
and
-bit
arithmetic for the additions and multiplications, respectively.)
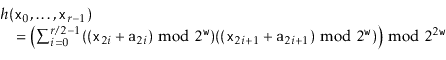
The method from Section 5.3.3 of using polynomials over prime fields
to hash variable-length arrays and strings is due to Dietzfelbinger et al. [22]. Due to its use of the 
operator which relies
on a costly machine instruction, it is, unfortunately, not very fast.
Some variants of this method choose the prime
to be one of the form
, in which case the 
operator can be replaced with
addition (
) and bitwise-and (
) operations [47, Section 3.6].
Another option is to apply one of the fast methods for fixed-length
strings to blocks of length 
for some constant 
and then apply
the prime field method to the resulting sequence of
hash codes.
and
.
, there exists
values that all have
the same hash code. (Hint: This is easy, and doesn't require any
number theory.)
, describe
values that all
have the same hash code. (Hint: This is harder, and requires
some basic number theory.)
in Lemma 5.1 is
the best possible bound by showing that, if
and
, then
. (Hint look
at the binary representations of
and
and use the fact
that
.)
to a
, which simply stores
in the
first
array entry it finds. Explain why this could be very slow
by giving an example of a sequence of
,
,
and
operations that would take on the order of
time to execute.
bool addSlow(T x) {
if (2*(q+1) > t.length) resize(); // max 50% occupancy
int i = hash(x);
while (t[i] != null) {
if (t[i] != del && x.equals(t[i])) return false;
i = (i == t.length-1) ? 0 : i + 1; // increment i
}
t[i] = x;
n++; q++;
return true;
}
method for the
class
worked by not using all of the characters found in long strings. For
example, for a sixteen character string, the hash code was computed
using only the eight even-indexed characters. Explain why this was a
very bad idea by giving an example of large set of strings that all
have the same hash code.
-bit integers,
and
.
Show why
does not make a good hash code for your object.
Give an example of a large set of objects that would all have hash
code 0.
-bit integers,
and
.
Show why
does not make a good hash code for your object.
Give an example of a large set of objects that would all have the same
hash code.
-bit integers,
and
. Suppose that the hash code for your object is defined
by some deterministic function
that produces a single
-bit integer. Prove that there exists a large set of objects that
have the same hash code.
for some positive integer
. Explain why, for a
positive integer 
by
repeatedly setting
.)
or the
or
implementations in this book,
and design a program that stores integers in this data
structure so that there are integers,
, such that
takes
linear time. That is, find a set of
integers for which there are
elements that hash to the same table location.
Depending on how good the implementation is, you may be able to do this just by inspecting the code for the implementation, or you may have to write some code that does trial insertions and searches, timing how long it takes to add and find particular values. (This can be, and has been, used to launch denial of service attacks on web servers [17].)