Next: 14.3 Discussion and Exercises Up: 14. External Memory Searching Previous: 14.1 The Block Store Contents Index
In this section, we discuss a generalization of binary trees,
called ![]() -trees, which is efficient in the external memory model.
Alternatively,
-trees, which is efficient in the external memory model.
Alternatively, ![]() -trees can be viewed as the natural generalization of
2-4 trees described in Section 9.1. (A 2-4 tree is a special case
of a
-trees can be viewed as the natural generalization of
2-4 trees described in Section 9.1. (A 2-4 tree is a special case
of a ![]() -tree that we get by setting
-tree that we get by setting ![]() .)
.)
For any integer ![]() , a
, a ![]() -tree is a tree in which all of
the leaves have the same depth and every non-root internal node,
-tree is a tree in which all of
the leaves have the same depth and every non-root internal node,
![]() ,
has at least
,
has at least ![]() children and at most
children and at most ![]() children. The children of
children. The children of
![]() are stored in an array,
are stored in an array,
![]() . The required number of children is
relaxed at the root, which can have anywhere between 2 and
. The required number of children is
relaxed at the root, which can have anywhere between 2 and ![]() children.
children.
If the height of a ![]() -tree is
-tree is ![]() , then it follows that the number,
, then it follows that the number,
![]() , of leaves in the
, of leaves in the ![]() -tree satisfies
-tree satisfies
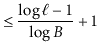 |
||
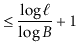 |
||
Each node,
![]() , in
, in ![]() -tree stores an array of keys
-tree stores an array of keys
![]() . If
. If
![]() is an internal node with
is an internal node with ![]() children, then the number of keys stored at
children, then the number of keys stored at
![]() is exactly
is exactly ![]() and these
are stored in
and these
are stored in
![]() . The remaining
. The remaining ![]() array entries in
array entries in
![]() are set to
are set to
![]() . If
. If
![]() is a non-root leaf
node, then
is a non-root leaf
node, then
![]() contains between
contains between ![]() and
and ![]() keys. The keys in a
keys. The keys in a
![]() -tree respect an order similar to the keys in a binary search tree.
For any node,
-tree respect an order similar to the keys in a binary search tree.
For any node,
![]() , that stores
, that stores ![]() keys,
keys,
Note that the data stored in a ![]() -tree node has size
-tree node has size ![]() . Therefore,
in an external memory setting, the value of
. Therefore,
in an external memory setting, the value of ![]() in a
in a ![]() -tree is chosen
so that a node fits into a single external memory block. In this way,
the time it takes to perform a
-tree is chosen
so that a node fits into a single external memory block. In this way,
the time it takes to perform a ![]() -tree operation in the external memory
model is proportional to the number of nodes that are accessed (read or
written) by the operation.
-tree operation in the external memory
model is proportional to the number of nodes that are accessed (read or
written) by the operation.
For example, if the keys are 4 byte integers and the node indices are
also 4 bytes, then setting ![]() means that each node stores
means that each node stores
The
![]() class, which implements a
class, which implements a ![]() -tree, stores a
-tree, stores a
![]() ,
,
![]() , that stores
, that stores
![]() nodes as well as the index,
nodes as well as the index,
![]() , of the
root node. As usual, an integer,
, of the
root node. As usual, an integer,
![]() , is used to keep track of the number
of items in the data structure:
, is used to keep track of the number
of items in the data structure:
int n; // number of elements stored in the tree int ri; // index of the root BlockStore<Node*> bs;
The implementation of the
![]() operation, which is illustrated in
Figure 14.3, generalizes the
operation, which is illustrated in
Figure 14.3, generalizes the
![]() operation in a binary
search tree. The search for
operation in a binary
search tree. The search for
![]() starts at the root and uses the keys
stored at a node,
starts at the root and uses the keys
stored at a node,
![]() , to determine in which of
, to determine in which of
![]() 's children the search
should continue.
's children the search
should continue.
![\includegraphics[width=\textwidth ]{figs/btree-2}](img6290.png) |
T find(T x) {
T z = null;
int ui = ri;
while (ui >= 0) {
Node *u = bs.readBlock(ui);
int i = findIt(u->keys, x);
if (i < 0) return u->keys[-(i+1)]; // found it
if (u->keys[i] != null)
z = u->keys[i];
ui = u->children[i];
}
return z;
}
Central to the
int findIt(array<T> &a, T x) {
int lo = 0, hi = a.length;
while (hi != lo) {
int m = (hi+lo)/2;
int cmp = a[m] == null ? -1 : compare(x, a[m]);
if (cmp < 0)
hi = m; // look in first half
else if (cmp > 0)
lo = m+1; // look in second half
else
return -m-1; // found it
}
return lo;
}
The
We can analyze the running time of a ![]() -tree
-tree
![]() operation both
in the usual word-RAM model (where every instruction counts) and in the
external memory model (where we only count the number of nodes accessed).
Since each leaf in a
operation both
in the usual word-RAM model (where every instruction counts) and in the
external memory model (where we only count the number of nodes accessed).
Since each leaf in a ![]() -tree stores at least one key and the height
of a
-tree stores at least one key and the height
of a ![]() -Tree with
-Tree with ![]() leaves is
leaves is
![]() , the height of a
, the height of a
![]() -tree that stores
-tree that stores
![]() keys is
keys is
![]() . Therefore, in the
external memory model, the time taken by the
. Therefore, in the
external memory model, the time taken by the
![]() operation is
operation is
![]() . To determine the running time in the word-RAM model,
we have to account for the cost of calling
. To determine the running time in the word-RAM model,
we have to account for the cost of calling
![]() for each node
we access, so the running time of
for each node
we access, so the running time of
![]() in the word-RAM model is
in the word-RAM model is
One important difference between ![]() -trees and the
-trees and the
![]() data structure from Section 6.2 is that the nodes of a
data structure from Section 6.2 is that the nodes of a
![]() -tree do not store pointers to their parents. The reason for this
will be explained shortly. The lack of parent pointers means that
the
-tree do not store pointers to their parents. The reason for this
will be explained shortly. The lack of parent pointers means that
the
![]() and
and
![]() operations on
operations on ![]() -trees are most easily
implemented using recursion.
-trees are most easily
implemented using recursion.
Like all balanced search trees, some form of rebalancing is required
during an
![]() operation. In a
operation. In a ![]() -tree, this is done by
splitting nodes.
Refer to Figure 14.5 for what follows.
Although splitting takes place across two levels of recursion, it is
best understood as an operation that takes a node
-tree, this is done by
splitting nodes.
Refer to Figure 14.5 for what follows.
Although splitting takes place across two levels of recursion, it is
best understood as an operation that takes a node
![]() containing
containing ![]() keys and having
keys and having ![]() children. It creates a new node,
children. It creates a new node,
![]() , that
adopts
, that
adopts
![]() . The new node
. The new node
![]() also takes
also takes
![]() 's
's ![]() largest keys,
largest keys,
![]() .
At this point,
.
At this point,
![]() has
has ![]() children and
children and ![]() keys. The extra key,
keys. The extra key,
![]() , is passed up to the parent of
, is passed up to the parent of
![]() , which also adopts
, which also adopts
![]() .
.
Notice that the splitting operation modifies three nodes:
![]() ,
,
![]() 's
parent, and the new node,
's
parent, and the new node,
![]() . This is why it is important that the
nodes of a
. This is why it is important that the
nodes of a ![]() -tree do not maintain parent pointers. If they did, then
the
-tree do not maintain parent pointers. If they did, then
the ![]() children adopted by
children adopted by
![]() would all need to have their parent
pointers modified. This would increase the number of external memory
accesses from 3 to
would all need to have their parent
pointers modified. This would increase the number of external memory
accesses from 3 to ![]() and would make
and would make ![]() -trees much less efficient for
large values of
-trees much less efficient for
large values of ![]() .
.
The
![]() method in a
method in a ![]() -tree is illustrated in Figure 14.6.
At a high level, this method finds a leaf,
-tree is illustrated in Figure 14.6.
At a high level, this method finds a leaf,
![]() , at which to add the
value
, at which to add the
value
![]() . If this causes
. If this causes
![]() to become overfull (because it already
contained
to become overfull (because it already
contained ![]() keys), then
keys), then
![]() is split. If this causes
is split. If this causes
![]() 's parent to
become overfull, then
's parent to
become overfull, then
![]() 's parent is also split, which may cause
's parent is also split, which may cause
![]() 's
grandparent to become overfull, and so on. This process continues,
moving up the tree one level at a time until reaching a node that
is not overfull or until the root is split. In the former case, the
process stops. In the latter case, a new root is created whose two
children become the nodes obtained when the original root was split.
's
grandparent to become overfull, and so on. This process continues,
moving up the tree one level at a time until reaching a node that
is not overfull or until the root is split. In the former case, the
process stops. In the latter case, a new root is created whose two
children become the nodes obtained when the original root was split.
The executive summary of the
![]() method is that it walks
from the root to a leaf searching for
method is that it walks
from the root to a leaf searching for
![]() , adds
, adds
![]() to this leaf, and
then walks back up to the root, splitting any overfull nodes it encounters
along the way. With this high level view in mind, we can now delve into
the details of how this method can be implemented recursively.
to this leaf, and
then walks back up to the root, splitting any overfull nodes it encounters
along the way. With this high level view in mind, we can now delve into
the details of how this method can be implemented recursively.
The real work of
![]() is done by the
is done by the
![]() method,
which adds the value
method,
which adds the value
![]() to the subtree whose root,
to the subtree whose root,
![]() , has the
identifier
, has the
identifier
![]() . If
. If
![]() is a leaf, then
is a leaf, then
![]() is simply inserted into
is simply inserted into
![]() . Otherwise,
. Otherwise,
![]() is added recursively into the appropriate
child,
is added recursively into the appropriate
child,
![]() , of
, of
![]() . The result of this recursive call is normally
. The result of this recursive call is normally
![]() but may also be a reference to a newly-created node,
but may also be a reference to a newly-created node,
![]() , that
was created because
, that
was created because
![]() was split. In this case,
was split. In this case,
![]() adopts
adopts
![]() and takes its first key, completing the splitting operation on
and takes its first key, completing the splitting operation on
![]() .
.
After the value
![]() has been added (either to
has been added (either to
![]() or to a descendant of
or to a descendant of
![]() ),
the
),
the
![]() method checks to see if
method checks to see if
![]() is storing too many
(more than
is storing too many
(more than ![]() ) keys. If so, then
) keys. If so, then
![]() needs to be split
with a call to the
needs to be split
with a call to the
![]() method. The result of calling
method. The result of calling
![]() is a new node that is used as the return value for
is a new node that is used as the return value for
![]() .
.
Node* addRecursive(T x, int ui) {
Node *u = bs.readBlock(ui);
int i = findIt(u->keys, x);
if (i < 0) throw(-1);
if (u->children[i] < 0) { // leaf node, just add it
u->add(x, -1);
bs.writeBlock(u->id, u);
} else {
Node* w = addRecursive(x, u->children[i]);
if (w != NULL) { // child was split, w is new child
x = w->remove(0);
bs.writeBlock(w->id, w);
u->add(x, w->id);
bs.writeBlock(u->id, u);
}
}
return u->isFull() ? u->split() : NULL;
}
The
![]() method is a helper for the
method is a helper for the
![]() method, which
calls
method, which
calls
![]() to insert
to insert
![]() into the root of the
into the root of the ![]() -tree.
If
-tree.
If
![]() causes the root to split, then a new root is
created that takes as its children both the old root and the new node
created by the splitting of the old root.
causes the root to split, then a new root is
created that takes as its children both the old root and the new node
created by the splitting of the old root.
bool add(T x) {
Node *w;
try {
w = addRecursive(x, ri);
} catch (int e) {
return false; // adding duplicate value
}
if (w != NULL) { // root was split, make new root
Node *newroot = new Node(this);
x = w->remove(0);
bs.writeBlock(w->id, w);
newroot->children[0] = ri;
newroot->keys[0] = x;
newroot->children[1] = w->id;
ri = newroot->id;
bs.writeBlock(ri, newroot);
}
n++;
return true;
}
The
![]() method and its helper,
method and its helper,
![]() , can be analyzed
in two phases:
, can be analyzed
in two phases:
Recall that the value of ![]() can be quite large, much larger
than even
can be quite large, much larger
than even
![]() . Therefore, in the word-RAM model, adding a value
to a
. Therefore, in the word-RAM model, adding a value
to a ![]() -tree can be much slower than adding into a balanced binary
search tree. Later, in Section 14.2.4, we will show that the
situation is not quite so bad; the amortized number of split operations
done during an
-tree can be much slower than adding into a balanced binary
search tree. Later, in Section 14.2.4, we will show that the
situation is not quite so bad; the amortized number of split operations
done during an
![]() operation is constant. This shows that the
(amortized) running time of the
operation is constant. This shows that the
(amortized) running time of the
![]() operation in the word-RAM model
is
operation in the word-RAM model
is
![]() .
.
The
![]() operation in a
operation in a
![]() is, again, most easily implemented
as a recursive method. Although the recursive implementation of
is, again, most easily implemented
as a recursive method. Although the recursive implementation of
![]() spreads the complexity across several methods, the overall
process, which is illustrated in Figure 14.7, is fairly
straightforward. By shuffling keys around, removal is reduced to the
problem of removing a value,
spreads the complexity across several methods, the overall
process, which is illustrated in Figure 14.7, is fairly
straightforward. By shuffling keys around, removal is reduced to the
problem of removing a value,
![]() , from some leaf,
, from some leaf,
![]() . Removing
. Removing
![]() may leave
may leave
![]() with less than
with less than ![]() keys; this situation is called
an underflow.
keys; this situation is called
an underflow.
When an underflow occurs,
![]() either borrows keys from, or is merged with,
one of its siblings. If
either borrows keys from, or is merged with,
one of its siblings. If
![]() is merged with a sibling, then
is merged with a sibling, then
![]() 's parent
will now have one less child and one less key, which can cause
's parent
will now have one less child and one less key, which can cause
![]() 's
parent to underflow; this is again corrected by borrowing or merging,
but merging may cause
's
parent to underflow; this is again corrected by borrowing or merging,
but merging may cause
![]() 's grandparent to underflow. This process
works its way back up to the root until there is no more underflow or
until the root has its last two children merged into a single child.
When the latter case occurs, the root is removed and its lone child
becomes the new root.
's grandparent to underflow. This process
works its way back up to the root until there is no more underflow or
until the root has its last two children merged into a single child.
When the latter case occurs, the root is removed and its lone child
becomes the new root.
Next we delve into the details of how each of these steps is implemented.
The first job of the
![]() method is to find the element
method is to find the element
![]() that
should be removed. If
that
should be removed. If
![]() is found in a leaf, then
is found in a leaf, then
![]() is removed from
this leaf. Otherwise, if
is removed from
this leaf. Otherwise, if
![]() is found at
is found at
![]() for some internal
node,
for some internal
node,
![]() , then the algorithm removes the smallest value,
, then the algorithm removes the smallest value,
![]() , in the
subtree rooted at
, in the
subtree rooted at
![]() . The value
. The value
![]() is the smallest
value stored in the
is the smallest
value stored in the
![]() that is greater than
that is greater than
![]() . The value of
. The value of
![]() is then used to replace
is then used to replace
![]() in
in
![]() . This process is illustrated
in Figure 14.8.
. This process is illustrated
in Figure 14.8.
|
The
![]() method is a recursive implementation of the
preceding algorithm:
method is a recursive implementation of the
preceding algorithm:
T removeSmallest(int ui) {
Node* u = bs.readBlock(ui);
if (u->isLeaf())
return u->remove(0);
T y = removeSmallest(u->children[0]);
checkUnderflow(u, 0);
return y;
}
bool removeRecursive(T x, int ui) {
if (ui < 0) return false; // didn't find it
Node* u = bs.readBlock(ui);
int i = findIt(u->keys, x);
if (i < 0) { // found it
i = -(i+1);
if (u->isLeaf()) {
u->remove(i);
} else {
u->keys[i] = removeSmallest(u->children[i+1]);
checkUnderflow(u, i+1);
}
return true;
} else if (removeRecursive(x, u->children[i])) {
checkUnderflow(u, i);
return true;
}
return false;
}
Note that, after recursively removing the value
![]() from the
from the
![]() th child of
th child of
![]() ,
,
![]() needs to ensure that this child still has at
least
needs to ensure that this child still has at
least ![]() keys. In the preceding code, this is done using a
method called
keys. In the preceding code, this is done using a
method called
![]() , which checks for and corrects an
underflow in the
, which checks for and corrects an
underflow in the
![]() th child of
th child of
![]() . Let
. Let
![]() be the
be the
![]() th child of
th child of
![]() .
If
.
If
![]() has only
has only ![]() keys, then this needs to be fixed. The fix
requires using a sibling of
keys, then this needs to be fixed. The fix
requires using a sibling of
![]() . This can be either child
. This can be either child
![]() of
of
![]() or child
or child
![]() of
of
![]() . We will usually use child
. We will usually use child
![]() of
of
![]() ,
which is the sibling,
,
which is the sibling,
![]() , of
, of
![]() directly to its left. The only time
this doesn't work is when
directly to its left. The only time
this doesn't work is when
![]() , in which case we use the sibling
directly to
, in which case we use the sibling
directly to
![]() 's right.
's right.
void checkUnderflow(Node* u, int i) {
if (u->children[i] < 0) return;
if (i == 0)
checkUnderflowZero(u, i); // use u's right sibling
else
checkUnderflowNonZero(u, i);
}
In the following, we focus on the case when
To fix an underflow at node
![]() , we need to find more keys (and possibly
also children), for
, we need to find more keys (and possibly
also children), for
![]() . There are two ways to do this:
. There are two ways to do this:
void checkUnderflowZero(Node *u, int i) {
Node *w = bs.readBlock(u->children[i]);
if (w->size() < B-1) { // underflow at w
Node *v = bs.readBlock(u->children[i+1]);
if (v->size() > B) { // w can borrow from v
shiftRL(u, i, v, w);
} else { // w will absorb w
merge(u, i, w, v);
u->children[i] = w->id;
}
}
}
void checkUnderflowNonZero(Node *u, int i) {
Node *w = bs.readBlock(u->children[i]);
if (w->size() < B-1) { // underflow at w
Node *v = bs.readBlock(u->children[i-1]);
if (v->size() > B) { // w can borrow from v
shiftLR(u, i-1, v, w);
} else { // v will absorb w
merge(u, i-1, v, w);
}
}
}
To summarize, the
![]() method in a
method in a ![]() -tree follows a root to
leaf path, removes a key
-tree follows a root to
leaf path, removes a key
![]() from a leaf,
from a leaf,
![]() , and then performs zero
or more merge operations involving
, and then performs zero
or more merge operations involving
![]() and its ancestors, and performs
at most one borrowing operation. Since each merge and borrow operation
involves modifying only three nodes, and only
and its ancestors, and performs
at most one borrowing operation. Since each merge and borrow operation
involves modifying only three nodes, and only
![]() of these
operations occur, the entire process takes
of these
operations occur, the entire process takes
![]() time in the
external memory model. Again, however, each merge and borrow operation
takes
time in the
external memory model. Again, however, each merge and borrow operation
takes ![]() time in the word-RAM model, so (for now) the most we can
say about the running time required by
time in the word-RAM model, so (for now) the most we can
say about the running time required by
![]() in the word-RAM model
is that it is
in the word-RAM model
is that it is
![]() .
.
Thus far, we have shown that
The following lemma shows that, so far, we have overestimated the number of merge and split operations performed by ![]() -trees.
-trees.
To keep track of these credits the proof maintains the following
credit invariant:
Any non-root node with ![]() keys stores one
credit and any node with
keys stores one
credit and any node with ![]() keys stores three credits. A node
that stores at least
keys stores three credits. A node
that stores at least ![]() keys and most
keys and most ![]() keys need not store
any credits. What remains is to show that we can maintain the credit
invariant and satisfy properties 1 and 2, above, during each
keys need not store
any credits. What remains is to show that we can maintain the credit
invariant and satisfy properties 1 and 2, above, during each
![]() and
and
![]() operation.
operation.
![]()
Each split operation occurs because a key is added to a node,
![]() , that
already contains
, that
already contains ![]() keys. When this happens,
keys. When this happens,
![]() is split into two
nodes,
is split into two
nodes,
![]() and
and
![]() having
having ![]() and
and ![]() keys, respectively. Prior to
this operation,
keys, respectively. Prior to
this operation,
![]() was storing
was storing ![]() keys, and hence three credits.
Two of these credits can be used to pay for the split and the other
credit can be given to
keys, and hence three credits.
Two of these credits can be used to pay for the split and the other
credit can be given to
![]() (which has
(which has ![]() keys) to maintain the
credit invariant. Therefore, we can pay for the split and maintain
the credit invariant during any split.
keys) to maintain the
credit invariant. Therefore, we can pay for the split and maintain
the credit invariant during any split.
The only other modification to nodes that occur during an
![]() operation happens after all splits, if any, are complete. This
modification involves adding a new key to some node
operation happens after all splits, if any, are complete. This
modification involves adding a new key to some node
![]() . If, prior
to this,
. If, prior
to this,
![]() had
had ![]() children, then it now has
children, then it now has ![]() children and
must therefore receive three credits. These are the only credits given
out by the
children and
must therefore receive three credits. These are the only credits given
out by the
![]() method.
method.
After any merges are performed, at most one borrow operation occurs,
after which no further merges or borrows occur. This borrow operation
only occurs if we remove a key from a leaf,
![]() , that has
, that has ![]() keys.
The node
keys.
The node
![]() therefore has one credit, and this credit goes towards
the cost of the borrow. This single credit is not enough to pay for
the borrow, so we create one credit to complete the payment.
therefore has one credit, and this credit goes towards
the cost of the borrow. This single credit is not enough to pay for
the borrow, so we create one credit to complete the payment.
At this point, we have created one credit and we still need to show
that the credit invariant can be maintained. In the worst case,
![]() 's sibling,
's sibling,
![]() , has exactly
, has exactly ![]() keys before the borrow so that,
afterwards, both
keys before the borrow so that,
afterwards, both
![]() and
and
![]() have
have ![]() keys. This means that
keys. This means that
![]() and
and
![]() each should be storing a credit when the operation is complete.
Therefore, in this case, we create an additional two credits to give to
each should be storing a credit when the operation is complete.
Therefore, in this case, we create an additional two credits to give to
![]() and
and
![]() . Since a borrow happens at most once during a
. Since a borrow happens at most once during a
![]() operation, this means that we create at most three credits, as required.
operation, this means that we create at most three credits, as required.
If the
![]() operation does not include a borrow operation, this
is because it finishes by removing a key from some node that, prior
to the operation, had
operation does not include a borrow operation, this
is because it finishes by removing a key from some node that, prior
to the operation, had ![]() or more keys. In the worst case, this node
had exactly
or more keys. In the worst case, this node
had exactly ![]() keys, so that it now has
keys, so that it now has ![]() keys and must be given
one credit, which we create.
keys and must be given
one credit, which we create.
In either case--whether the removal finishes with a borrow
operation or not--at most three credits need to be created during a
call to
![]() to maintain the credit invariant and pay for all
borrows and merges that occur. This completes the proof of the lemma.
to maintain the credit invariant and pay for all
borrows and merges that occur. This completes the proof of the lemma.
The purpose of Lemma 14.1 is to show that, in the word-RAM
model the cost of splits, merges and joins during a sequence of ![]()
![]() and
and
![]() operations is only
operations is only ![]() . That is, the
amortized cost per operation is only
. That is, the
amortized cost per operation is only ![]() , so the amortized cost
of
, so the amortized cost
of
![]() and
and
![]() in the word-RAM model is
in the word-RAM model is
![]() .
This is summarized by the following pair of theorems:
.
This is summarized by the following pair of theorems:
opendatastructures.org