The external memory model of computation was introduced by Aggarwal and
Vitter [4]. It is sometimes also called the I/O model
or the disk access model.
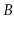 -Trees are to external memory searching what binary search trees
are to internal memory searching.
-Trees are to external memory searching what binary search trees
are to internal memory searching. 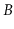 -trees were introduced by Bayer
and McCreight [9] in 1970 and, less than ten years later, the
title of Comer's ACM Computing Surveys article referred to
them as ubiquitous [15].
-trees were introduced by Bayer
and McCreight [9] in 1970 and, less than ten years later, the
title of Comer's ACM Computing Surveys article referred to
them as ubiquitous [15].
Like binary search trees, there are many variants of 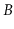 -Trees, including
-Trees, including
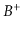 -trees,
-trees,
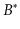 -trees,
and counted
-trees,
and counted 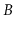 -trees.
-trees.
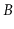 -trees are indeed
ubiquitous and are the primary data structure in many file systems,
including Apple's HFS+,
Microsoft's NTFS,
and Linux's Ext4;
every
major database system; and key-value stores used in cloud computing.
Graefe's recent survey [36] provides a 200+ page overview of the
many modern applications, variants, and optimizations of
-trees are indeed
ubiquitous and are the primary data structure in many file systems,
including Apple's HFS+,
Microsoft's NTFS,
and Linux's Ext4;
every
major database system; and key-value stores used in cloud computing.
Graefe's recent survey [36] provides a 200+ page overview of the
many modern applications, variants, and optimizations of 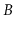 -trees.
-trees.
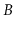 -trees implement the
-trees implement the
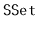 interface. If only the
interface. If only the
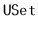 interface
is needed, then external memory hashing
could be used as an alternative
to
interface
is needed, then external memory hashing
could be used as an alternative
to 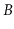 -trees. External memory hashing schemes do exist; see, for example,
Jensen and Pagh [43]. These schemes implement the
-trees. External memory hashing schemes do exist; see, for example,
Jensen and Pagh [43]. These schemes implement the
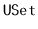 operations
in
operations
in 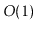 expected time in the external memory model. However, for a
variety of reasons, many applications still use
expected time in the external memory model. However, for a
variety of reasons, many applications still use 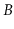 -trees even though
they only require
-trees even though
they only require
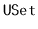 operations.
operations.
One reason 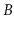 -trees are such a popular choice is that they often perform
better than their
-trees are such a popular choice is that they often perform
better than their
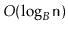 running time bounds suggest. The
reason for this is that, in external memory settings, the value of
running time bounds suggest. The
reason for this is that, in external memory settings, the value of 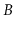 is typically quite large--in the hundreds or even thousands. This means
that 99% or even 99.9% of the data in a
is typically quite large--in the hundreds or even thousands. This means
that 99% or even 99.9% of the data in a 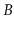 -tree is stored in the
leaves. In a database system with a large memory, it may be possible
to cache all the internal nodes of a
-tree is stored in the
leaves. In a database system with a large memory, it may be possible
to cache all the internal nodes of a 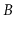 -tree in RAM, since they only
represent 1% or 0.1% of the total data set. When this happens,
this means that a search in a
-tree in RAM, since they only
represent 1% or 0.1% of the total data set. When this happens,
this means that a search in a 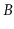 -tree involves a very fast search in
RAM, through the internal nodes, followed by a single external memory
access to retrieve a leaf.
-tree involves a very fast search in
RAM, through the internal nodes, followed by a single external memory
access to retrieve a leaf.
Exercise 14..1
Show what happens when the keys 1.5 and then 7.5 are added to the
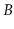
-tree in Figure
14.2.
Exercise 14..2
Show what happens when the keys 3 and then 4 are removed from the
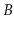
-tree in Figure
14.2.
Exercise 14..3
What is the maximum number of internal nodes in a
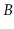
-tree that stores
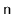
keys (as a function of
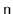
and
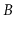
)?
Exercise 14..5
Draw the credits used in the proof of Lemma
14.1 on the trees
in Figures
14.6 and
14.7. Verify
that (with three additional credits) it is possible to pay for the splits,
merges, and borrows and maintain the credit invariant.
Exercise 14..6
Design a modified version of a
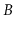
-tree in which nodes can have anywhere
from
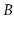
up to
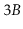
children (and hence
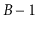
up to
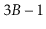
keys).
Show that this new version of
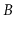
-trees performs only
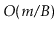
splits,
merges, and borrows during a sequence of
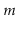
operations. (Hint:
For this to work, you will have to be more agressive with merging,
sometimes merging two nodes before it is strictly necessary.)
Exercise 14..7
In this exercise, you will design a modified method of splitting and
merging in
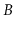
-trees that asymptotically reduces the number of splits,
borrows and merges by considering up to three nodes at a time.
- Let
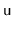 be an overfull node and let
be an overfull node and let
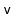 be a sibling immediately
to the right of
be a sibling immediately
to the right of
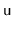 . There are two ways to fix the overflow at
. There are two ways to fix the overflow at
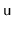 :
:
-
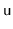 can give some of its keys to
can give some of its keys to
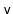 ; or
; or
-
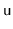 can be split and the keys of
can be split and the keys of
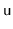 and
and
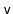 can be evenly
distributed among
can be evenly
distributed among
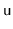 ,
,
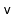 , and the newly created node,
, and the newly created node,
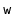 .
.
Show that this can always be done in such a way that, after the
operation, each of the (at most 3) affected nodes has at least
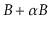 keys and at most
keys and at most
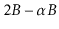 keys, for some constant
keys, for some constant
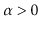 .
.
- Let
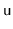 be an underfull node and let
be an underfull node and let
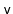 and
and
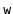 be siblings of
be siblings of
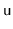 There are two ways to fix the underflow at
There are two ways to fix the underflow at
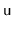 :
:
- keys can be redistributed among
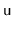 ,
,
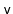 , and
, and
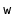 ; or
; or
-
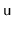 ,
,
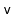 , and
, and
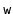 can be merged into two nodes and the keys
of
can be merged into two nodes and the keys
of
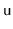 ,
,
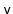 , and
, and
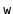 can be redistributed amongst these nodes.
can be redistributed amongst these nodes.
Show that this can always be done in such a way that, after the
operation, each of the (at most 3) affected nodes has at least
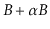 keys and at most
keys and at most
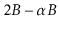 keys, for some constant
keys, for some constant
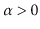 .
.
- Show that, with these modifications, the number of
merges, borrows, and splits that occur during
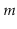 operations is
operations is 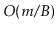 .
.
Exercise 14..8
A
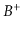
-tree, illustrated in Figure
14.11 stores every key in a
leaf and keeps its leaves stored as a doubly-linked list. As usual,
each leaf stores between
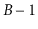
and
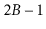
keys. Above this list is
a standard
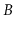
-tree that stores the largest value from each leaf but
the last.
- Describe fast implementations of
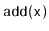 ,
,
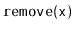 ,
and
,
and
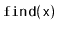 in a
in a 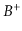 -tree.
-tree.
- Explain how to efficiently implement the
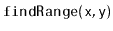 method,
that reports all values
greater than
method,
that reports all values
greater than
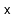 and less than or equal to
and less than or equal to
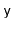 , in
a
, in
a 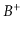 -tree.
-tree.
- Implement a class,
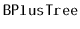 , that implements
, that implements
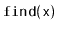 ,
,
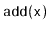 ,
,
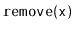 , and
, and
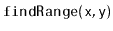 .
.
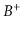 -trees duplicate some of the keys because they are stored
both in the
-trees duplicate some of the keys because they are stored
both in the 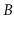 -tree and in the list. Explain why this duplication
does not add up to much for large values of
-tree and in the list. Explain why this duplication
does not add up to much for large values of 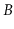 .
.
opendatastructures.org
![]() -Trees are to external memory searching what binary search trees
are to internal memory searching.
-Trees are to external memory searching what binary search trees
are to internal memory searching. ![]() -trees were introduced by Bayer
and McCreight [9] in 1970 and, less than ten years later, the
title of Comer's ACM Computing Surveys article referred to
them as ubiquitous [15].
-trees were introduced by Bayer
and McCreight [9] in 1970 and, less than ten years later, the
title of Comer's ACM Computing Surveys article referred to
them as ubiquitous [15].
![]() -Trees, including
-Trees, including
![]() -trees,
-trees,
![]() -trees,
and counted
-trees,
and counted ![]() -trees.
-trees.
![]() -trees are indeed
ubiquitous and are the primary data structure in many file systems,
including Apple's HFS+,
Microsoft's NTFS,
and Linux's Ext4;
every
major database system; and key-value stores used in cloud computing.
Graefe's recent survey [36] provides a 200+ page overview of the
many modern applications, variants, and optimizations of
-trees are indeed
ubiquitous and are the primary data structure in many file systems,
including Apple's HFS+,
Microsoft's NTFS,
and Linux's Ext4;
every
major database system; and key-value stores used in cloud computing.
Graefe's recent survey [36] provides a 200+ page overview of the
many modern applications, variants, and optimizations of ![]() -trees.
-trees.
![]() -trees implement the
-trees implement the
![]() interface. If only the
interface. If only the
![]() interface
is needed, then external memory hashing
could be used as an alternative
to
interface
is needed, then external memory hashing
could be used as an alternative
to ![]() -trees. External memory hashing schemes do exist; see, for example,
Jensen and Pagh [43]. These schemes implement the
-trees. External memory hashing schemes do exist; see, for example,
Jensen and Pagh [43]. These schemes implement the
![]() operations
in
operations
in ![]() expected time in the external memory model. However, for a
variety of reasons, many applications still use
expected time in the external memory model. However, for a
variety of reasons, many applications still use ![]() -trees even though
they only require
-trees even though
they only require
![]() operations.
operations.
![]() -trees are such a popular choice is that they often perform
better than their
-trees are such a popular choice is that they often perform
better than their
![]() running time bounds suggest. The
reason for this is that, in external memory settings, the value of
running time bounds suggest. The
reason for this is that, in external memory settings, the value of ![]() is typically quite large--in the hundreds or even thousands. This means
that 99% or even 99.9% of the data in a
is typically quite large--in the hundreds or even thousands. This means
that 99% or even 99.9% of the data in a ![]() -tree is stored in the
leaves. In a database system with a large memory, it may be possible
to cache all the internal nodes of a
-tree is stored in the
leaves. In a database system with a large memory, it may be possible
to cache all the internal nodes of a ![]() -tree in RAM, since they only
represent 1% or 0.1% of the total data set. When this happens,
this means that a search in a
-tree in RAM, since they only
represent 1% or 0.1% of the total data set. When this happens,
this means that a search in a ![]() -tree involves a very fast search in
RAM, through the internal nodes, followed by a single external memory
access to retrieve a leaf.
-tree involves a very fast search in
RAM, through the internal nodes, followed by a single external memory
access to retrieve a leaf.