9.3 Summary

The following theorem summarizes the performance of the $\mathtt{RedBlackTree}$ data structure:

Theorem 9..1   A $\mathtt{RedBlackTree}$ implements the $\mathtt{SSet}$ interface. A $\mathtt{RedBlackTree}$ supports the operations $\mathtt{add(x)}$, $\mathtt{remove(x)}$, and $\mathtt{find(x)}$ in $O(\log \ensuremath{\mathtt{n}})$ worst-case time per operation.

Not included in the above theorem is the extra bonus

Theorem 9..2   Beginning with an empty $\mathtt{RedBlackTree}$, any sequence of $m$ $\mathtt{add(x)}$ and $\mathtt{remove(x)}$ operations results in a total of $O(m)$ time spent during all calls $\mathtt{addFixup(u)}$ and $\mathtt{removeFixup(u)}$.

We will only sketch a proof of Theorem 9.2. By comparing $\mathtt{addFixup(u)}$ and $\mathtt{removeFixup(u)}$ with the algorithms for adding or removing a leaf in a 2-4 tree, we can convince ourselves that this property is something that is inherited from a 2-4 tree. In particular, if we can show that the total time spent splitting, merging, and borrowing in a 2-4 tree is $O(m)$, then this implies Theorem 9.2.

The proof of this for 2-4 trees uses the potential method of amortized analysis.² Define the potential of an internal node $\mathtt{u}$ in a 2-4 tree as

$$\Phi(\ensuremath{\mathtt{u}}) = \begin{cases} 1 & \text{if \en... ...ildren} \\ 3 & \text{if \ensuremath{\mathtt{u}} has 4 children} \end{cases}$$

and the potential of a 2-4 tree as the sum of the potentials of its nodes. When a split occurs, it is because a node of degree 4 becomes two nodes, one of degree 2 and one of degree 3. This means that the overall potential drops by $3-1-0 = 2$. When a merge occurs, two nodes that used to have degree 2 are replaced by one node of degree 3. The result is a drop in potential of $2-0=2$. Therefore, for every split or merge, the potential decreases by $2$.

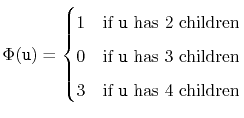
Next notice that, if we ignore splitting and merging of nodes, there are only a constant number of nodes whose number of children is changed by the addition or removal of a leaf. When adding a node, one node has its number of children increase by 1, increasing the potential by at most $3$. During the removal of a leaf, one node has its number of children decrease by 1, increasing the potential by at most $1$, and two nodes may be involved in a borrowing operation, increasing their total potential by at most $1$.

To summarize, each merge and split causes the potential to drop by at least 2. Ignoring merging and splitting, each addition or removal causes the potential to rise by at most 3, and the potential is always non-negative. Therefore, the number of splits and merges caused by $m$ additions or removals on an initially empty tree is at most $3m/2$. Theorem 9.2 is a consequence of this analysis and the correspondence between 2-4 trees and red-black trees.

Footnotes

... analysis.²

See the proofs of Lemma 2.2 and Lemma 3.1 for other applications of the potential method.