Next: 10.3 Discussion and Exercises Up: 10. Heaps Previous: 10.1 : An Implicit Contents Index
: A Randomized Meldable Heap
In this section, we describe the
, a priority
implementation in which the underlying structure is also a heap-ordered
binary tree. However, unlike a
in which the underlying
binary tree is completely defined by the number of elements, there
are no restrictions on the shape of the binary tree that underlies
a
; anything goes.
The
and
operations in a
are
implemented in terms of the
operation. This operation
takes two heap nodes
and
and merges them, returning a heap
node that is the root of a heap that contains all elements in the subtree
rooted at
and all elements in the subtree rooted at
.
The nice thing about a
operation is that it can be
defined recursively. See Figure 10.4. If either
or
is
, then we are merging with an empty set, so we return
or
, respectively. Otherwise, assume
since,
if
, then we can reverse the roles of
and
.
Then we know that the root of the merged heap will contain
, and
we can recursively merge
with
or
, as we wish.
This is where randomization comes in, and we toss a coin to decide
whether to merge
with
or
:
Node* merge(Node *h1, Node *h2) {
if (h1 == nil) return h2;
if (h2 == nil) return h1;
if (compare(h1->x, h2->x) > 0) return merge(h2, h1);
// now we know h1->x <= h2->x
if (rand() % 2) {
h1->left = merge(h1->left, h2);
if (h1->left != nil) h1->left->parent = h1;
} else {
h1->right = merge(h1->right, h2);
if (h1->right != nil) h1->right->parent = h1;
}
return h1;
}
In the next section, we show that
runs in
expected time, where
is the total number of elements in
and
.
With access to a
operation, the
operation is easy. We create a new node
containing
and then merge
with the root of our heap:
![\includegraphics[width=\textwidth ]{figs/meldable-merge}](img4659.png)
bool add(T x) {
Node *u = new Node();
u->left = u->right = u->parent = nil;
u->x = x;
r = merge(u, r);
r->parent = nil;
n++;
return true;
}
This takes
expected time.
The
operation is similarly easy. The node we want to remove
is the root, so we just merge its two children and make the result the root:
T remove() {
T x = r->x;
Node *tmp = r;
r = merge(r->left, r->right);
delete tmp;
if (r != nil) r->parent = nil;
n--;
return x;
}
Again, this takes
expected time.
Additionally, a
can implement many other operations in
expected time, including:
: remove the node
(and its key
) from the heap.
: add all the elements of the
to this heap, emptying
in the process.
operations that each take
expected time.
The analysis of
is based on the analysis of a random walk
in a binary tree. A random walk in a binary tree starts at the
root of the tree. At each step in the random walk, a coin is tossed and,
depending on the result of this coin toss, the walk proceeds to the left
or to the right child of the current node. The walk ends when it falls
off the tree (the current node becomes
).
The following lemma is somewhat remarkable because it does not depend at all on the shape of the binary tree:
. In the base case,
and the walk
has length
. Suppose now that the result is true for
all non-negative integers
.
Let
denote the size of the root's left subtree, so that
is the size of the root's right subtree. Starting at
the root, the walk takes one step and then continues in a subtree of
size
or
. By our inductive hypothesis, the expected
length of the walk is then
![$\displaystyle \mathrm{E}[W] = 1 + \frac{1}{2}\log (\ensuremath{\mathtt{n}}_1+1) + \frac{1}{2}\log (\ensuremath{\mathtt{n}}_2+1) \enspace ,
$](img4703.png)
and
are less than
. Since 
is a concave function,
![$ \mathrm{E}[W]$](img4708.png){kind=small}
is maximized when
.
Therefore,
the expected number of steps taken by the random walk is
![$\displaystyle \mathrm{E}[W]$](img4710.png){kind=small} |
 |
|
 |
||
 |
||
 |
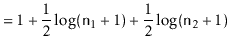We make a quick digression to note that, for readers who know a little about information theory, the proof of Lemma 10.1 can be stated in terms of entropy.
denote the depth of the 
th external node and recall that a
binary tree with
nodes has
external nodes. The probability
of the random walk reaching the 
th external node is exactly
, so the expected length of the random walk is given by
elements. A basic
fact about the entropy of a distribution over
elements is that
it does not exceed
, which proves the lemma.
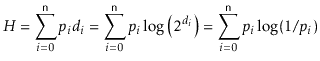
With this result on random walks, we can now easily prove that the
running time of the
operation is
.
and
are the roots of two heaps containing
and
nodes, respectively, then the expected running time of
is at most
, where
.
or the heap rooted at
.
The algorithm terminates when either of these two random walks fall
out of its corresponding tree (when
or
).
Therefore, the expected number of steps performed by the merge algorithm
is at most
The following theorem summarizes the performance of a
:
implements the (priority)
interface.
A
supports the operations
and
in
expected time per operation.opendatastructures.org
