• 3 Linked Lists
• 3.1 SLList: A Singly-Linked List
• 3.1.1 Queue Operations
• 3.1.2 Summary
• 3.2 DLList: A Doubly-Linked List
• 3.2.1 Adding and Removing
• 3.2.2 Summary
• 3.3 SEList: A Space-Efficient Linked List
• 3.3.1 Space Requirements
• 3.3.2 Finding Elements
• 3.3.3 Adding an Element
• 3.3.4 Removing an Element
• 3.3.5 Amortized Analysis of Spreading and Gathering
• 3.3.6 Summary
• 3.4 Discussion and Exercises

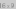
In this chapter, we continue to study implementations of the List interface, this time using pointer-based data structures rather than arrays. The structures in this chapter are made up of nodes that contain the list items. Using references (pointers), the nodes are linked together into a sequence. We first study singly-linked lists, which can implement Stack and (FIFO) Queue operations in constant time per operation and then move on to doubly-linked lists, which can implement Deque operations in constant time.

Linked lists have advantages and disadvantages when compared to array-based implementations of the List interface. The primary disadvantage is that we lose the ability to access any element using get(i) or set(i,x) in constant time. Instead, we have to walk through the list, one element at a time, until we reach the ith element. The primary advantage is that they are more dynamic: Given a reference to any list node u, we can delete u or insert a node adjacent to u in constant time. This is true no matter where u is in the list.

3.1 SLList: A Singly-Linked List

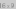
An SLList (singly-linked list) is a sequence of Nodes. Each node u stores a data value u.x and a reference u.next to the next node in the sequence. For the last node w in the sequence, \(\texttt{w.next} = \texttt{null}\)

    class Node {
        T x;
        Node next;
    }

For efficiency, an SLList uses variables head and tail to keep track of the first and last node in the sequence, as well as an integer n to keep track of the length of the sequence:

    Node head;
    Node tail;
    int n;

Figure 3.1 A sequence of Queue (add(x) and remove()) and Stack (push(x) and pop()) operations on an SLList.

An SLList can efficiently implement the Stack operations push() and pop() by adding and removing elements at the head of the sequence. The push() operation simply creates a new node u with data value x, sets u.next to the old head of the list and makes u the new head of the list. Finally, it increments n since the size of the SLList has increased by one:

    T push(T x) {
        Node u = new Node();
        u.x = x;
        u.next = head;
        head = u;
        if (n == 0)
            tail = u;
        n++;
        return x;
    }

The pop() operation, after checking that the SLList is not empty, removes the head by setting \(\texttt{head=head.next}\) and decrementing n. A special case occurs when the last element is being removed, in which case tail is set to null:

    T pop() {
        if (n == 0)    return null;
        T x = head.x;
        head = head.next;
        if (--n == 0) tail = null;
        return x;
    }    

Clearly, both the push(x) and pop() operations run in \(O(1)\) time.

3.1.1 Queue Operations

An SLList can also implement the FIFO queue operations add(x) and remove() in constant time. Removals are done from the head of the list, and are identical to the pop() operation:

    T remove() {
        if (n == 0)    return null;
        T x = head.x;
        head = head.next;
        if (--n == 0) tail = null;
        return x;
    }    

Additions, on the other hand, are done at the tail of the list. In most cases, this is done by setting \(\texttt{tail.next}=\texttt{u}\), where u is the newly created node that contains x. However, a special case occurs when \(\texttt{n}=0\), in which case \(\texttt{tail}=\texttt{head}=\texttt{null}\). In this case, both tail and head are set to u.

    boolean add(T x) {
        Node u = new Node();
        u.x = x;
        if (n == 0) {
            head = u;
        } else {
            tail.next = u;
        }
        tail = u;
        n++;
        return true;
    }

Clearly, both add(x) and remove() take constant time.

3.1.2 Summary

The following theorem summarizes the performance of an SLList:

An SLList nearly implements the full set of Deque operations. The only missing operation is removing from the tail of an SLList. Removing from the tail of an SLList is difficult because it requires updating the value of tail so that it points to the node w that precedes tail in the SLList; this is the node w such that \(\texttt{w.next}=\texttt{tail}\). Unfortunately, the only way to get to w is by traversing the SLList starting at head and taking \(\texttt{n}-2\) steps.

3.2 DLList: A Doubly-Linked List

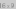
A DLList (doubly-linked list) is very similar to an SLList except that each node u in a DLList has references to both the node u.next that follows it and the node u.prev that precedes it.

    class Node {
        T x;
        Node prev, next;
    }

When implementing an SLList, we saw that there were always several special cases to worry about. For example, removing the last element from an SLList or adding an element to an empty SLList requires care to ensure that head and tail are correctly updated. In a DLList, the number of these special cases increases considerably. Perhaps the cleanest way to take care of all these special cases in a DLList is to introduce a dummy node. This is a node that does not contain any data, but acts as a placeholder so that there are no special nodes; every node has both a next and a prev, with dummy acting as the node that follows the last node in the list and that precedes the first node in the list. In this way, the nodes of the list are (doubly-)linked into a cycle, as illustrated in Figure 3.2.

Figure 3.2 A DLList containing a,b,c,d,e.

    int n;
    Node dummy;
    DLList() {
        dummy = new Node();
        dummy.next = dummy;
        dummy.prev = dummy;
        n = 0;
    }

Finding the node with a particular index in a DLList is easy; we can either start at the head of the list (dummy.next) and work forward, or start at the tail of the list (dummy.prev) and work backward. This allows us to reach the ith node in \(O(1+\min\{\texttt{i},\texttt{n}-\texttt{i}\})\) time:

    Node getNode(int i) {
        Node p = null;
        if (i < n / 2) {
            p = dummy.next;
            for (int j = 0; j < i; j++)
                p = p.next;
        } else {
            p = dummy;
            for (int j = n; j > i; j--)
                p = p.prev;
        }
        return p;
    }

The get(i) and set(i,x) operations are now also easy. We first find the ith node and then get or set its x value:

    T get(int i) {
        return getNode(i).x;
    }
    T set(int i, T x) {
        Node u = getNode(i);
        T y = u.x;
        u.x = x;
        return y;
    }

The running time of these operations is dominated by the time it takes to find the ith node, and is therefore \(O(1+\min\{\texttt{i},\texttt{n}-\texttt{i}\})\).

3.2.1 Adding and Removing

If we have a reference to a node w in a DLList and we want to insert a node u before w, then this is just a matter of setting \(\texttt{u.next}=\texttt{w}\), \(\texttt{u.prev}=\texttt{w.prev}\), and then adjusting u.prev.next and u.next.prev. (See Figure 3.3.) Thanks to the dummy node, there is no need to worry about w.prev or w.next not existing.

    Node addBefore(Node w, T x) {
        Node u = new Node();
        u.x = x;
        u.prev = w.prev;
        u.next = w;
        u.next.prev = u;
        u.prev.next = u;
        n++;
        return u;
    }

Figure 3.3 Adding the node u before the node w in a DLList.

Now, the list operation add(i,x) is trivial to implement. We find the ith node in the DLList and insert a new node u that contains x just before it.

    void add(int i, T x) {
        addBefore(getNode(i), x);
    }

The only non-constant part of the running time of add(i,x) is the time it takes to find the ith node (using getNode(i)). Thus, add(i,x) runs in \(O(1+\min\{\texttt{i}, \texttt{n}-\texttt{i}\})\) time.

Removing a node w from a DLList is easy. We only need to adjust pointers at w.next and w.prev so that they skip over w. Again, the use of the dummy node eliminates the need to consider any special cases:

    void remove(Node w) {
        w.prev.next = w.next;
        w.next.prev = w.prev;
        n--;
    }

Now the remove(i) operation is trivial. We find the node with index i and remove it:

    T remove(int i) {
        Node w = getNode(i);
        remove(w);
        return w.x;
    }

Again, the only expensive part of this operation is finding the ith node using getNode(i), so remove(i) runs in \(O(1+\min\{\texttt{i}, \texttt{n}-\texttt{i}\})\) time.

3.2.2 Summary

The following theorem summarizes the performance of a DLList:

It is worth noting that, if we ignore the cost of the getNode(i) operation, then all operations on a DLList take constant time. Thus, the only expensive part of operations on a DLList is finding the relevant node. Once we have the relevant node, adding, removing, or accessing the data at that node takes only constant time.

This is in sharp contrast to the array-based List implementations of Chapter 2; in those implementations, the relevant array item can be found in constant time. However, addition or removal requires shifting elements in the array and, in general, takes non-constant time.

For this reason, linked list structures are well-suited to applications where references to list nodes can be obtained through external means. An example of this is the LinkedHashSet data structure found in the Java Collections Framework, in which a set of items is stored in a doubly-linked list and the nodes of the doubly-linked list are stored in a hash table (discussed in Chapter 5). When elements are removed from a LinkedHashSet, the hash table is used to find the relevant list node in constant time and then the list node is deleted (also in constant time).

3.3 SEList: A Space-Efficient Linked List

One of the drawbacks of linked lists (besides the time it takes to access elements that are deep within the list) is their space usage. Each node in a DLList requires an additional two references to the next and previous nodes in the list. Two of the fields in a Node are dedicated to maintaining the list, and only one of the fields is for storing data!

An SEList (space-efficient list) reduces this wasted space using a simple idea: Rather than store individual elements in a DLList, we store a block (array) containing several items. More precisely, an SEList is parameterized by a block size b. Each individual node in an SEList stores a block that can hold up to b+1 elements.

For reasons that will become clear later, it will be helpful if we can do Deque operations on each block. The data structure that we choose for this is a BDeque (bounded deque), derived from the ArrayDeque structure described in Section 2.4. The BDeque differs from the ArrayDeque in one small way: When a new BDeque is created, the size of the backing array a is fixed at b+1 and never grows or shrinks. The important property of a BDeque is that it allows for the addition or removal of elements at either the front or back in constant time. This will be useful as elements are shifted from one block to another.

    class BDeque extends ArrayDeque<T> {
        BDeque() {
            super(SEList.this.f.type());
            a = f.newArray(b+1);
        }
        void resize() { }
    }

An SEList is then a doubly-linked list of blocks:

    class Node {
        BDeque d;
        Node prev, next;
    }

    int n;
    Node dummy;

3.3.1 Space Requirements

An SEList places very tight restrictions on the number of elements in a block: Unless a block is the last block, then that block contains at least \(\texttt{b}-1\) and at most \(\texttt{b}+1\) elements. This means that, if an SEList contains n elements, then it has at most \begin{equation*} \texttt{n}/(\texttt{b}-1) + 1 = O(\texttt{n}/\texttt{b}) \end{equation*} blocks. The BDeque for each block contains an array of length \(\texttt{b}+1\) but, for every block except the last, at most a constant amount of space is wasted in this array. The remaining memory used by a block is also constant. This means that the wasted space in an SEList is only \(O(\texttt{b}+\texttt{n}/\texttt{b})\). By choosing a value of b within a constant factor of \(\sqrt{\texttt{n}}\), we can make the space-overhead of an SEList approach the \(\sqrt{\texttt{n}}\) lower bound given in Section 2.6.2.

3.3.2 Finding Elements

The first challenge we face with an SEList is finding the list item with a given index i. Note that the location of an element consists of two parts:

1. The node u that contains the block that contains the element with index i; and
2. the index j of the element within its block.

    class Location {
        Node u;
        int j;
        Location(Node u, int j) {
            this.u = u;
            this.j = j;
        }
    }

To find the block that contains a particular element, we proceed the same way as we do in a DLList. We either start at the front of the list and traverse in the forward direction, or at the back of the list and traverse backwards until we reach the node we want. The only difference is that, each time we move from one node to the next, we skip over a whole block of elements.

    Location getLocation(int i) {
        if (i < n/2) {
            Node u = dummy.next;
            while (i >= u.d.size()) {
                i -= u.d.size();
                u = u.next;
            }
            return new Location(u, i);
        } else {
            Node u = dummy;
            int idx = n;
            while (i < idx) {
                u = u.prev;
                idx -= u.d.size();
            }
            return new Location(u, i-idx);
        }
    }

Remember that, with the exception of at most one block, each block contains at least \(\texttt{b}-1\) elements, so each step in our search gets us \(\texttt{b}-1\) elements closer to the element we are looking for. If we are searching forward, this means that we reach the node we want after \(O(1+\texttt{i}/\texttt{b})\) steps. If we search backwards, then we reach the node we want after \(O(1+(\texttt{n}-\texttt{i})/\texttt{b})\) steps. The algorithm takes the smaller of these two quantities depending on the value of i, so the time to locate the item with index i is \(O(1+\min\{\texttt{i},\texttt{n}-\texttt{i}\}/\texttt{b})\).

Once we know how to locate the item with index i, the get(i) and set(i,x) operations translate into getting or setting a particular index in the correct block:

    T get(int i) {
        Location l = getLocation(i);
        return l.u.d.get(l.j);
    }
    T set(int i, T x) {
        Location l = getLocation(i);
        T y = l.u.d.get(l.j);
        l.u.d.set(l.j,x);
        return y;
    }

The running times of these operations are dominated by the time it takes to locate the item, so they also run in \(O(1+\min\{\texttt{i},\texttt{n}-\texttt{i}\}/\texttt{b})\) time.

3.3.3 Adding an Element

Adding elements to an SEList is a little more complicated. Before considering the general case, we consider the easier operation, add(x), in which x is added to the end of the list. If the last block is full (or does not exist because there are no blocks yet), then we first allocate a new block and append it to the list of blocks. Now that we are sure that the last block exists and is not full, we append x to the last block.

    boolean add(T x) {
        Node last = dummy.prev;
        if (last == dummy || last.d.size() == b+1) {
            last = addBefore(dummy);
        }
        last.d.add(x);
        n++;
        return true;
    }

Things get more complicated when we add to the interior of the list using add(i,x). We first locate i to get the node u whose block contains the ith list item. The problem is that we want to insert x into u's block, but we have to be prepared for the case where u's block already contains \(\texttt{b}+1\) elements, so that it is full and there is no room for x.

Let \(\texttt{u}_0,\texttt{u}_1,\texttt{u}_2,\ldots\) denote u, u.next, u.next.next, and so on. We explore \(\texttt{u}_0,\texttt{u}_1,\texttt{u}_2,\ldots\) looking for a node that can provide space for x. Three cases can occur during our space exploration (see Figure 3.4):

[4ex]

[4ex]

Figure 3.4 The three cases that occur during the addition of an item x in the interior of an SEList. (This SEList has block size \(\texttt{b}=3\).)

1. We quickly (in \(r+1\le \texttt{b}\) steps) find a node \(\texttt{u}_r\) whose block is not full. In this case, we perform \(r\) shifts of an element from one block into the next, so that the free space in \(\texttt{u}_r\) becomes a free space in \(\texttt{u}_0\). We can then insert x into \(\texttt{u}_0\)'s block.

2. We quickly (in \(r+1\le \texttt{b}\) steps) run off the end of the list of blocks. In this case, we add a new empty block to the end of the list of blocks and proceed as in the first case.

3. After b steps we do not find any block that is not full. In this case, \(\texttt{u}_0,\ldots,\texttt{u}_{\texttt{b}-1}\) is a sequence of b blocks that each contain \(\texttt{b}+1\) elements. We insert a new block \(\texttt{u}_{\texttt{b}}\) at the end of this sequence and spread the original \(\texttt{b}(\texttt{b}+1)\) elements so that each block of \(\texttt{u}_0,\ldots,\texttt{u}_{\texttt{b}}\) contains exactly b elements. Now \(\texttt{u}_0\)'s block contains only b elements so it has room for us to insert x.

    void add(int i, T x) {
        if (i == n) {
            add(x);
            return;
        }
        Location l = getLocation(i);
        Node u = l.u;
        int r = 0;
        while (r < b && u != dummy && u.d.size() == b+1) {
            u = u.next;
            r++;
        }
        if (r == b) {      // b blocks each with b+1 elements
            spread(l.u);
            u = l.u;
        } 
        if (u == dummy) {  // ran off the end - add new node
            u = addBefore(u);
        }
        while (u != l.u) { // work backwards, shifting elements
            u.d.add(0, u.prev.d.remove(u.prev.d.size()-1));
            u = u.prev;
        }
        u.d.add(l.j, x);
        n++;
    }

The running time of the add(i,x) operation depends on which of the three cases above occurs. Cases 1 and 2 involve examining and shifting elements through at most b blocks and take \(O(\texttt{b})\) time. Case 3 involves calling the spread(u) method, which moves \(\texttt{b}(\texttt{b}+1)\) elements and takes \(O(\texttt{b}^2)\) time. If we ignore the cost of Case 3 (which we will account for later with amortization) this means that the total running time to locate i and perform the insertion of x is \(O(\texttt{b}+\min\{\texttt{i},\texttt{n}-\texttt{i}\}/\texttt{b})\).

3.3.4 Removing an Element

Removing an element from an SEList is similar to adding an element. We first locate the node u that contains the element with index i. Now, we have to be prepared for the case where we cannot remove an element from u without causing u's block to become smaller than \(\texttt{b}-1\).

Again, let \(\texttt{u}_0,\texttt{u}_1,\texttt{u}_2,\ldots\) denote u, u.next, u.next.next, and so on. We examine \(\texttt{u}_0,\texttt{u}_1,\texttt{u}_2,\ldots\) in order to look for a node from which we can borrow an element to make the size of \(\texttt{u}_0\)'s block at least \(\texttt{b}-1\). There are three cases to consider (see Figure 3.5):

[4ex]

[4ex]

Figure 3.5 The three cases that occur during the removal of an item x in the interior of an SEList. (This SEList has block size \(\texttt{b}=3\).)

1. We quickly (in \(r+1\le \texttt{b}\) steps) find a node whose block contains more than \(\texttt{b}-1\) elements. In this case, we perform \(r\) shifts of an element from one block into the previous one, so that the extra element in \(\texttt{u}_r\) becomes an extra element in \(\texttt{u}_0\). We can then remove the appropriate element from \(\texttt{u}_0\)'s block.

2. We quickly (in \(r+1\le \texttt{b}\) steps) run off the end of the list of blocks. In this case, \(\texttt{u}_r\) is the last block, and there is no need for \(\texttt{u}_r\)'s block to contain at least \(\texttt{b}-1\) elements. Therefore, we proceed as above, borrowing an element from \(\texttt{u}_r\) to make an extra element in \(\texttt{u}_0\). If this causes \(\texttt{u}_r\)'s block to become empty, then we remove it.

3. After b steps, we do not find any block containing more than \(\texttt{b}-1\) elements. In this case, \(\texttt{u}_0,\ldots,\texttt{u}_{\texttt{b}-1}\) is a sequence of b blocks that each contain \(\texttt{b}-1\) elements. We gather these \(\texttt{b}(\texttt{b}-1)\) elements into \(\texttt{u}_0,\ldots,\texttt{u}_{\texttt{b}-2}\) so that each of these \(\texttt{b}-1\) blocks contains exactly b elements and we remove \(\texttt{u}_{\texttt{b}-1}\), which is now empty. Now \(\texttt{u}_0\)'s block contains b elements and we can then remove the appropriate element from it.

    T remove(int i) {
        Location l = getLocation(i);
        T y = l.u.d.get(l.j);
        Node u = l.u;
        int r = 0;
        while (r < b && u != dummy && u.d.size() == b-1) {
            u = u.next;
            r++;
        }
        if (r == b) {  // b blocks each with b-1 elements
            gather(l.u);
        }
        u = l.u;
        u.d.remove(l.j);
        while (u.d.size() < b-1 && u.next != dummy) {
            u.d.add(u.next.d.remove(0));
            u = u.next;
        }
        if (u.d.isEmpty()) remove(u);
        n--;
        return y;
    }

Like the add(i,x) operation, the running time of the remove(i) operation is \(O(\texttt{b}+\min\{\texttt{i},\texttt{n}-\texttt{i}\}/\texttt{b})\) if we ignore the cost of the gather(u) method that occurs in Case 3.

3.3.5 Amortized Analysis of Spreading and Gathering

Next, we consider the cost of the gather(u) and spread(u) methods that may be executed by the add(i,x) and remove(i) methods. For the sake of completeness, here they are:

    void spread(Node u) {
        Node w = u;
        for (int j = 0; j < b; j++) {
            w = w.next;
        }
        w = addBefore(w);
        while (w != u) {
            while (w.d.size() < b)
                w.d.add(0,w.prev.d.remove(w.prev.d.size()-1));
            w = w.prev;
        }
    }

    void gather(Node u) {
        Node w = u;
        for (int j = 0; j < b-1; j++) {
            while (w.d.size() < b)
                w.d.add(w.next.d.remove(0));
            w = w.next;
        }
        remove(w);
    }

The running time of each of these methods is dominated by the two nested loops. Both the inner and outer loops execute at most \(\texttt{b}+1\) times, so the total running time of each of these methods is \(O((\texttt{b}+1)^2)=O(\texttt{b}^2)\). However, the following lemma shows that these methods execute on at most one out of every b calls to add(i,x) or remove(i).

3.3.6 Summary

The following theorem summarizes the performance of the SEList data structure:

The SEList is a trade-off between an ArrayList and a DLList where the relative mix of these two structures depends on the block size b. At the extreme \(\texttt{b}=2\), each SEList node stores at most three values, which is not much different than a DLList. At the other extreme, \(\texttt{b}>\texttt{n}\), all the elements are stored in a single array, just like in an ArrayList. In between these two extremes lies a trade-off between the time it takes to add or remove a list item and the time it takes to locate a particular list item.

3.4 Discussion and Exercises

Both singly-linked and doubly-linked lists are established techniques, having been used in programs for over 40 years. They are discussed, for example, by Knuth [46]. Even the SEList data structure seems to be a well-known data structures exercise. The SEList is sometimes referred to as an unrolled linked list [69].

Another way to save space in a doubly-linked list is to use so-called XOR-lists. In an XOR-list, each node, u, contains only one pointer, called u.nextprev, that holds the bitwise exclusive-or of u.prev and u.next. The list itself needs to store two pointers, one to the dummy node and one to dummy.next (the first node, or dummy if the list is empty). This technique uses the fact that, if we have pointers to u and u.prev, then we can extract u.next using the formula \begin{equation*} \texttt{u.next} = \texttt{u.prev} \verb+^+ \texttt{u.nextprev} \enspace . \end{equation*} (Here \verb+^+ computes the bitwise exclusive-or of its two arguments.) This technique complicates the code a little and is not possible in some languages, like Java and Python, that have garbage collection but gives a doubly-linked list implementation that requires only one pointer per node. See Sinha's magazine article [70] for a detailed discussion of XOR-lists.

The next few exercises involve performing manipulations on DLLists. You should complete them without allocating any new nodes or temporary arrays. They can all be done only by changing the prev and next values of existing nodes.

The next few exercises are more advanced and require a clear understanding of what happens to the minimum value stored in a Stack or Queue as items are added and removed.

The next exercises are designed to test the reader's understanding of the implementation and analysis of the space-efficient SEList: