Next: 8.2 Discussion and Exercises Up: 8. Scapegoat Trees Previous: 8. Scapegoat Trees Contents
: A Binary Search Tree with Partial Rebuilding
A
is a
that, in addition to keeping
track of the number,
, of nodes in the tree also keeps a counter,
,
that maintains an upper-bound on the number of nodes.
int q;At all times,
and
obey the following inequalities:
has logarithmic height; at all times, the height of the scapegoat tree does not exceed:
can look surprisingly unbalanced. The tree in Figure 8.1 has
and height
.
Implementing the
operation in a
is done
using the standard algorithm for searching in a
(see Section 6.2). This takes time proportional to the
height of the tree which, by (8.1) is
.
To implement the
operation, we first increment
and
and then use the usual algorithm for adding
to a binary search
tree; we search for
and then add a new leaf
with
.
At this point, we may get lucky and the depth of
might not exceed
. If so, then we leave well enough alone and don't do
anything else.
Unfortunately, it will sometimes happen that
. In this case we need to do something to reduce the height.
This isn't a big job; there is only one node, namely
, whose depth
exceeds
. To fix
, we walk from
back up to the
root looking for a scapegoat,
. The scapegoat,
, is a very
unbalanced node. It has the property that
is the child of
on the path from the root to
.
We'll very shortly prove that a scapegoat exists. For now, we can
take it for granted. Once we've found the scapegoat
, we completely
destroy the subtree rooted at
and rebuild it into a perfectly balanced
binary search tree. We know, from (8.2), that, even before
the addition of
,
's subtree was not a complete binary tree.
Therefore, when we rebuild
, the height decreases by at least 1 so that height of the
is once again at most
.
bool add(T x) {
// first do basic insertion keeping track of depth
Node *u = new Node;
u->x = x;
u->left = u->right = u->parent = nil;
int d = addWithDepth(u);
if (d > log32(q)) {
// depth exceeded, find scapegoat
Node *w = u->parent;
int a = BinaryTree<Node>::size(w);
int b = BinaryTree<Node>::size(w->parent);
while (3*a <= 2*b) {
w = w->parent;
a = BinaryTree<Node>::size(w);
b = BinaryTree<Node>::size(w->parent);
}
rebuild(w->parent);
}
return d >= 0;
}
|
and rebuilding the
subtree rooted at
, then the running time of
is dominated
by the initial search, which takes
time.
We will account for the cost of finding the scapegoat and rebuilding
using amortized analysis in the next section.
The implementation of
in a
is very simple.
We search for
and remove it using the usual algorithm for removing a
node from a
. (Note that this can never increase the
height of the tree.) Next, we decrement
but leave
unchanged.
Finally, we check if
and, if so, we rebuild the entire
tree into a perfectly balanced binary search tree and set
.
bool remove(T x) {
if (BinarySearchTree<Node,T>::remove(x)) {
if (2*n < q) {
rebuild(r);
q = n;
}
return true;
}
return false;
}
Again, if we ignore the cost of rebuilding, the running time of the
operation is proportional to the height of the tree, and is
therefore
.
In this section we analyze the correctness and amortized running time
of operations on a
. We first prove the correctness by
showing that, when the
operation results in a node that violates
Condition (8.1), then we can always find a scapegoat:
be a node of depth
in a
.
Then there exists a node
on the path from
to the root
such that
on the path from
to the root. Denote the path
from the root to
as
. Then, we have
,
,
and, more generally,
, hence
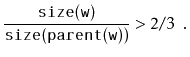
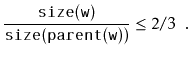
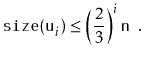
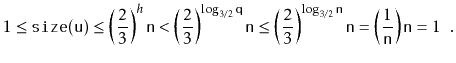
Next, we analyze the parts of the running time that we have not yet
accounted for. There are two parts: The cost of calls to
when search for scapegoat nodes, and the cost of calls to
when we find a scapegoat
. The cost of calls to
can be
related to the cost of calls to
, as follows:
in a
, the cost of finding the scapegoat
and rebuilding the subtree rooted at
is
.
, once we find it, is
. When searching for the scapegoat node, we call
on a sequence of nodes
until we find the scapegoat
. However, since
is the first node in this sequence
that is a scapegoat, we know that
. Therefore, the cost of all calls to
is
 |
 |
 |
|
|
 |
||
|
 |
||
|
 |
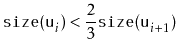
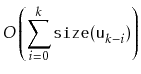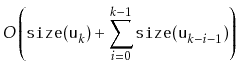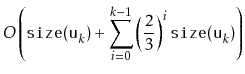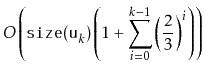All that remains is to prove an upper-bound on the cost of all calls to
during a sequence of 
operations:
any sequence of
and
operations causes at most
time to be used
by
operations.
, units of time spent rebuilding. The scheme gives out a total of
credits and every call to
is paid for with
credits stored at
.
During an insertion or deletion, we give one credit to each node on the
path to the inserted node, or deleted node,
. In this way we hand
out at most
credits per operation.
During a deletion we also store an additional 1 credit ``on the side.''
Thus, in total we give out at most
credits. All that
remains is to show that these credits are sufficient to pay for all
calls to
.
If we call
during an insertion, it is because
is
a scapegoat. Suppose, without loss of generality, that
was rebuilt (or when
was inserted, if a subtree containing
was never rebuilt), we had
or
operations that have
affected
or
since then is at least
that are available to pay for the
time it takes to
call
.
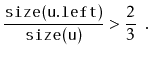
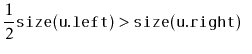
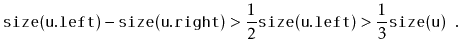
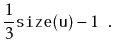
If we call
during a deletion, it is because
.
In this case, we have
credits stored ``on the side'' and
we use these to pay for the
time it takes to rebuild the root.
This completes the proof.
data structure:
implements the
interface. Ignoring the cost
of
operations, a
supports the operations
,
, and
in
time per operation.
Furthermore, beginning with an empty
, any sequence of
and
operations results in a total of
time spent during all calls to
.
opendatastructures.org