The term scapegoat tree is due to Galperin and Rivest [30],
who define and analyze these trees. However, the same structure
was discovered earlier by Andersson [4,6], who called them
general balanced trees since they can have any shape as long as
their height is small.
Experimenting with the
 implementation will reveal that
it is often considerably slower than the other
implementation will reveal that
it is often considerably slower than the other
 implementations
in this book. This may be somewhat surprising, since height bound of
implementations
in this book. This may be somewhat surprising, since height bound of
is better than the expected length of a search path in a
 and
not too far from that of a
and
not too far from that of a
 . The implementation could be optimized
by storing the sizes of subtrees explicitly at each node or by reusing
already computed subtree sizes (Exercises 8.5
and 8.6). Even with these optimizations,
there will always be sequences of
. The implementation could be optimized
by storing the sizes of subtrees explicitly at each node or by reusing
already computed subtree sizes (Exercises 8.5
and 8.6). Even with these optimizations,
there will always be sequences of
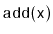 and
and
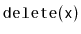 operation for
which a
operation for
which a
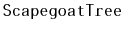 takes longer than other
takes longer than other
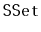 implementations.
implementations.
This gap in performance is due to the fact that, unlike the other
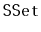 implementations discussed in this book, a
implementations discussed in this book, a
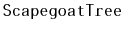 can spend a lot
of time restructuring itself. Exercise 8.3 asks you to prove
that there are sequences of
can spend a lot
of time restructuring itself. Exercise 8.3 asks you to prove
that there are sequences of
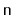 operations in which a
operations in which a
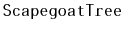 will spend on the order of
will spend on the order of
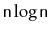 time in calls to
time in calls to
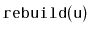 .
This is in contrast to other
.
This is in contrast to other
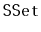 implementations discussed in this
book that only make
implementations discussed in this
book that only make
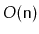 structural changes during a sequence of
structural changes during a sequence of
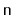 operations. This is, unfortunately, a necessary consequence of
the fact that a
operations. This is, unfortunately, a necessary consequence of
the fact that a
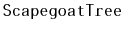 does all its restructuring by calls to
does all its restructuring by calls to
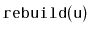 [17].
[17].
Despite their lack of performance, there are applications in which a
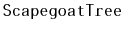 could be the right choice. This would occur any time
there is additional data associated with nodes that cannot be updated
in constant time when a rotation is performed, but that can be updated
during a
could be the right choice. This would occur any time
there is additional data associated with nodes that cannot be updated
in constant time when a rotation is performed, but that can be updated
during a
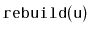 operation. In such cases, the
operation. In such cases, the
 and related structures based on partial rebuilding may work. An example of such an application is outlined in Exercise 8.12.
and related structures based on partial rebuilding may work. An example of such an application is outlined in Exercise 8.12.
Exercise 8..1
Illustrate the addition of the values 1.5 and then 1.6 on the
in Figure
8.1.
Exercise 8..2
Illustrate what happens when we start with an empty
and add the sequence
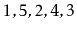
and show where the credits described
in the proof of Lemma
8.3 go, and how they are used
during this sequence of additions.
Exercise 8..3
Show that, if we start with an empty
and call
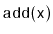
for
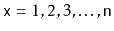
, then the total time spent during calls to
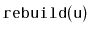
is at least
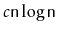
for some constant
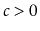
.
Exercise 8..5
Modify the
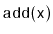
method of the
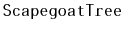
so that it does not
waste any time recomputing the sizes of subtrees that it has already
computed the size of. This is possible because, by the time the method
wants to compute
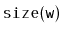
, it has already computed
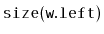
or
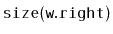
.
Compare the performance of your modified implementation with the
implementation given here.
Exercise 8..6
Implement a second version of the
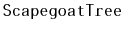
data structure that
explicitly stores and maintains the sizes of the subtree rooted at
each node. Compare the performance of the resulting implementation
with that of the original
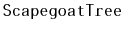
implementation as well as
the implementation from Exercise
8.5.
Exercise 8..7
Reimplement the
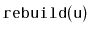
method discussed at the beginning of this
chapter so that it does not require the use of an array to store the
nodes of the subtree being rebuilt. Instead, it should use recursion
to first connect the nodes into a linked list and then convert this
linked list into a perfectly balanced binary tree. (There are
very elegant recursive implementations of both steps.)
Exercise 8..8
Analyze and implement a

. This is a tree in
which each node
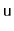
, except the root, maintains the
balance
invariant that
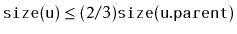
. The
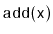
and
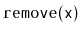
operations are identical to the standard

operations, except that any time the balance invariant is violated at
a node
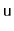
, the subtree rooted at
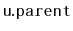
is rebuilt.
Your analysis should show that operations on a

run in
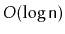
amortized time.
Exercise 8..9
Analyze and implement a

. This is a tree in
which each node
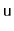
, except the root, maintains the
balance
invariant that
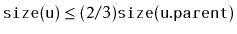
. The
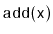
and
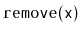
operations are identical to the standard

operations, except that any time the balance invariant is violated at
a node
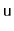
, rotations are performed in order to restore these invariants.
Your analysis should show that operations on a

run in
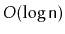
worst-case time.
Exercise 8..10
Analyze and implement a
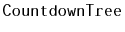
. In a
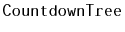
each
node
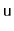
keeps a
timer
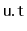
. The
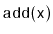
and
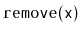
operations are exactly the same as in a standard

except that, whenever one of these operations affects
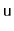
's subtree,
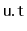
is decremented. When
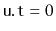
the entire subtree rooted at
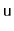
is rebuilt into a perfectly balanced binary search tree. When a node
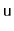
is involved in a rebuilding operation (either because
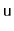
is rebuilt
or one of
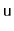
's ancestors is rebuilt)
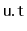
is reset to
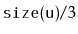
.
Your analysis should show that operations on a
 run
in
run
in
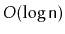 amortized time. (Hint: First show that each node
amortized time. (Hint: First show that each node
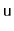 satisfies some version of a balance invariant.)
satisfies some version of a balance invariant.)
Exercise 8..11
Analyze and implement a
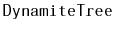
. In a
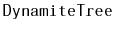
each
node
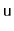
keeps tracks of the size of the subtree rooted at
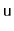
in a
variable
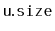
. The
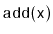
and
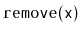
operations are exactly
the same as in a standard

except that, whenever one
of these operations affects a node
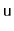
's subtree,
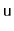 explodes
explodes
with probability
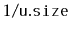
. When
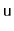
explodes, its entire subtree
is rebuilt into a perfectly balanced binary search tree.
Your analysis should show that operations on a
 run
in
run
in
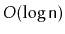 expected time.
expected time.
opendatastructures.org
![]() implementation will reveal that
it is often considerably slower than the other
implementation will reveal that
it is often considerably slower than the other
![]() implementations
in this book. This may be somewhat surprising, since height bound of
implementations
in this book. This may be somewhat surprising, since height bound of
![]() implementations discussed in this book, a
implementations discussed in this book, a
![]() can spend a lot
of time restructuring itself. Exercise 8.3 asks you to prove
that there are sequences of
can spend a lot
of time restructuring itself. Exercise 8.3 asks you to prove
that there are sequences of
![]() operations in which a
operations in which a
![]() will spend on the order of
will spend on the order of
![]() time in calls to
time in calls to
![]() .
This is in contrast to other
.
This is in contrast to other
![]() implementations discussed in this
book that only make
implementations discussed in this
book that only make
![]() structural changes during a sequence of
structural changes during a sequence of
![]() operations. This is, unfortunately, a necessary consequence of
the fact that a
operations. This is, unfortunately, a necessary consequence of
the fact that a
![]() does all its restructuring by calls to
does all its restructuring by calls to
![]() [17].
[17].
![]() could be the right choice. This would occur any time
there is additional data associated with nodes that cannot be updated
in constant time when a rotation is performed, but that can be updated
during a
could be the right choice. This would occur any time
there is additional data associated with nodes that cannot be updated
in constant time when a rotation is performed, but that can be updated
during a
![]() operation. In such cases, the
operation. In such cases, the
![]() and related structures based on partial rebuilding may work. An example of such an application is outlined in Exercise 8.12.
and related structures based on partial rebuilding may work. An example of such an application is outlined in Exercise 8.12.
![]() run
in
run
in
![]() amortized time. (Hint: First show that each node
amortized time. (Hint: First show that each node
![]() satisfies some version of a balance invariant.)
satisfies some version of a balance invariant.)![]() run
in
run
in
![]() expected time.
expected time. ![]() data structure can be implemented by storing the elements
in something like a
data structure can be implemented by storing the elements
in something like a
![]() , in the same order that they occur
in the sequence. To implement
, in the same order that they occur
in the sequence. To implement
![]() in constant time,
each element
in constant time,
each element
![]() is labelled with an integer that encodes the path from
the root to
is labelled with an integer that encodes the path from
the root to
![]() . In this way,
. In this way,
![]() can be implemented
just by comparing the labels of
can be implemented
just by comparing the labels of
![]() and
and
![]() .
.