Next: 12.4 Discussion and Exercises Up: 12. Graphs Previous: 12.2 : A Graph Contents
In this section we present two algorithms for exploring a graph, starting
at one of its vertices,
![]() , and finding all vertices that are reachable
from
, and finding all vertices that are reachable
from
![]() . Both of these algorithms are best suited to graphs represented
using an adjacency list representation. Therefore, when analyzing these
algorithms we will assume that the underlying representation is as an
. Both of these algorithms are best suited to graphs represented
using an adjacency list representation. Therefore, when analyzing these
algorithms we will assume that the underlying representation is as an
![]() .
.
The bread-first-search algorithm starts at a vertex
![]() and visits,
first the neighbours of
and visits,
first the neighbours of
![]() , then the neighbours of the neighbours of
, then the neighbours of the neighbours of
![]() ,
then the neighbours of the neighbours of the neighbours of
,
then the neighbours of the neighbours of the neighbours of
![]() , and so on.
, and so on.
This algorithm is a generalization of the breadth-first-search algorithm
for binary trees (Section 6.1.2), and is very similar; it
uses a queue,
![]() , that initially contains only
, that initially contains only
![]() . It then repeatedly
extracts an element from
. It then repeatedly
extracts an element from
![]() and adds its neighbours to
and adds its neighbours to
![]() , provided
that these neighbours have never been in
, provided
that these neighbours have never been in
![]() before. The only major difference
between breadth-first-search for graphs and for trees
is that the algorithm for graphs has to ensure that it does not
add the same vertex to
before. The only major difference
between breadth-first-search for graphs and for trees
is that the algorithm for graphs has to ensure that it does not
add the same vertex to
![]() more than once. It does this by using an
auxiliary boolean array,
more than once. It does this by using an
auxiliary boolean array,
![]() , that keeps track of which vertices have
already been discovered.
, that keeps track of which vertices have
already been discovered.
void bfs(Graph &g, int r) {
bool *seen = new bool[g.nVertices()];
SLList<int> q;
q.add(r);
seen[r] = true;
while (q.size() > 0) {
int i = q.remove();
ArrayStack<int> edges;
g.outEdges(i, edges);
for (int k = 0; k < edges.size(); k++) {
int j = edges.get(k);
if (!seen[j]) {
q.add(j);
seen[j] = true;
}
}
}
delete[] seen;
}
An example of running
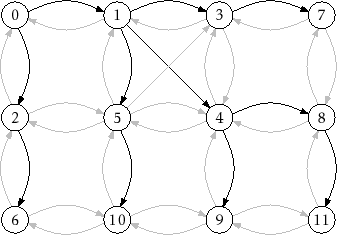
|
Analyzing the running-time of the
![]() routine is fairly
straightforward. The use of the
routine is fairly
straightforward. The use of the
![]() array ensures that no vertex is
added to
array ensures that no vertex is
added to
![]() more than once. Adding (and later removing) each vertex
from
more than once. Adding (and later removing) each vertex
from
![]() takes constant time per vertex for a total of
takes constant time per vertex for a total of
![]() time.
Since each vertex is processed at most once by the inner loop, each
adjacency list is processed at most once, so each edge of
time.
Since each vertex is processed at most once by the inner loop, each
adjacency list is processed at most once, so each edge of ![]() is processed
at most once. This processing, which is done in the inner loop takes
constant time per iteration, for a total of
is processed
at most once. This processing, which is done in the inner loop takes
constant time per iteration, for a total of
![]() time. Therefore,
the entire algorithm runs in
time. Therefore,
the entire algorithm runs in
![]() time.
time.
The following theorem summarizes the performance of the
![]() algorithm.
algorithm.
A breadth-first traversal has some very special properties. Calling
![]() will eventually enqueue (and eventually dequeue) every vertex
will eventually enqueue (and eventually dequeue) every vertex
![]() such that there is a directed path from
such that there is a directed path from
![]() to
to
![]() . Moreover,
the vertices at distance 0 from
. Moreover,
the vertices at distance 0 from
![]() (
(
![]() itself) will enter
itself) will enter
![]() before
the vertices at distance 1, which will enter
before
the vertices at distance 1, which will enter
![]() before the vertices at
distance 2, and so on. Thus, the
before the vertices at
distance 2, and so on. Thus, the
![]() method visits vertices
in increasing order of distance from
method visits vertices
in increasing order of distance from
![]() and vertices that can not be
reached from
and vertices that can not be
reached from
![]() are never output at all.
are never output at all.
A particularly useful application of the breadth-first-search algorithm
is, therefore, in computing shortest paths. To compute the shortest
path from
![]() to every other vertex, we use a variant of
to every other vertex, we use a variant of
![]() that uses an auxilliary array,
that uses an auxilliary array,
![]() , of length
, of length
![]() . When a new vertex
. When a new vertex
![]() is added to
is added to
![]() , we set
, we set
![]() . In this way,
. In this way,
![]() becomes the
second last node on a shortest path from
becomes the
second last node on a shortest path from
![]() to
to
![]() . Repeating this,
by taking
. Repeating this,
by taking
![]() ,
,
![]() , and so on we can reconstruct the
(reversal of) a shortest path from
, and so on we can reconstruct the
(reversal of) a shortest path from
![]() to
to
![]() .
.
The depth-first-search algorithm is similar to the standard algorithm for traversing binary trees; it first fully explores one subtree before returning to the current node and then exploring the other subtree. Another way to think of depth-first-search is by saying that it is similar to breadth-first search except that it uses a stack instead of a queue.
During the execution of the depth-first-search algorithm, each vertex,
![]() , is assigned a color,
, is assigned a color,
![]() :
:
![]() if we have never seen
the vertex before,
if we have never seen
the vertex before,
![]() if we are currently visiting that vertex,
and
if we are currently visiting that vertex,
and
![]() if we are done visiting that vertex. The easiest way to
think of depth-first-search is as a recursive algorithm. It starts by
visiting
if we are done visiting that vertex. The easiest way to
think of depth-first-search is as a recursive algorithm. It starts by
visiting
![]() . When visiting a vertex
. When visiting a vertex
![]() , we first mark
, we first mark
![]() as
as
![]() .
Next, we scan
.
Next, we scan
![]() 's adjacency list and recursively visit any white vertex
we find in this list. Finally, we are done processing
's adjacency list and recursively visit any white vertex
we find in this list. Finally, we are done processing
![]() , so we color
, so we color
![]() black and return.
black and return.
void dfs(Graph &g, int i, char *c) {
c[i] = grey; // currently visiting i
ArrayStack<int> edges;
g.outEdges(i, edges);
for (int k = 0; k < edges.size(); k++) {
int j = edges.get(k);
if (c[j] == white) {
c[j] = grey;
dfs(g, j, c);
}
}
c[i] = black; // done visiting i
}
void dfs(Graph &g, int r) {
char *c = new char[g.nVertices()];
dfs(g, r, c);
delete[] c;
}
An example of the execution of this algorithm is shown in Figure 12.5
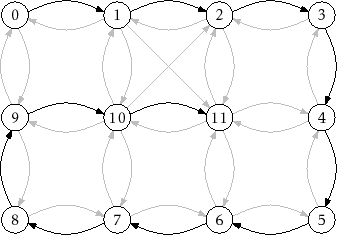
|
Although depth-first-search may best be thought of as a recursive
algorithm, recursion is not the best way to implement it. Indeed, the code
given above will fail for many large graphs by causing a stack overflow.
An alternative implementation is to replace the recursion stack with an
explicit stack,
![]() . The following implementation does just that:
. The following implementation does just that:
void dfs2(Graph &g, int r) {
char *c = new char[g.nVertices()];
SLList<int> s;
s.push(r);
while (s.size() > 0) {
int i = s.pop();
if (c[i] == white) {
c[i] = grey;
ArrayStack<int> edges;
g.outEdges(i, edges);
for (int k = 0; k < edges.size(); k++)
s.push(edges.get(k));
}
}
delete[] c;
}
In the above code, when next vertex,
Not surprisingly, the running times of
![]() and
and
![]() are the
same as that of
are the
same as that of
![]() :
:
As with the breadth-first-search algorithm, there is an underlying
tree associated with each execution of depth-first-search. When a node
![]() goes from
goes from
![]() to
to
![]() , this is because
, this is because
![]() was called recursively while processing some node
was called recursively while processing some node
![]() . (In the case
of
. (In the case
of
![]() algorithm,
algorithm,
![]() is one of the nodes that replaced
is one of the nodes that replaced
![]() on the stack.) If we think of
on the stack.) If we think of
![]() as the parent of
as the parent of
![]() , then we obtain
a tree rooted at
, then we obtain
a tree rooted at
![]() . In Figure 12.5, this tree is a path from
vertex 0 to vertex 11.
. In Figure 12.5, this tree is a path from
vertex 0 to vertex 11.
An important property of the depth-first-search algorithm is the
following: Suppose that when node
![]() is colored
is colored
![]() , there exists a path
from
, there exists a path
from
![]() to some other node
to some other node
![]() that uses only white vertices. Then
that uses only white vertices. Then
![]() will be colored (first
will be colored (first
![]() then)
then)
![]() before
before
![]() is colored
is colored
![]() .
(This can be proven by contradiction, by considering any path
.
(This can be proven by contradiction, by considering any path ![]() from
from
![]() to
to
![]() .)
.)
One application of this property is the detection of cycles. Refer
to Figure 12.6. Consider some cycle, ![]() , that can be reached
from
, that can be reached
from
![]() . Let
. Let
![]() be the first node of
be the first node of ![]() that is colored
that is colored
![]() ,
and let
,
and let
![]() be the node that precedes
be the node that precedes
![]() on the cycle
on the cycle ![]() . Then,
by the above property,
. Then,
by the above property,
![]() will be colored
will be colored
![]() and the edge
and the edge
![]() will be considered by the algorithm while
will be considered by the algorithm while
![]() is still
is still
![]() . Thus,
the algorithm can conclude that there is a path,
. Thus,
the algorithm can conclude that there is a path, ![]() , from
, from
![]() to
to
![]() in the depth-first-search tree and the edge
in the depth-first-search tree and the edge
![]() exists. Therefore,
exists. Therefore,
![]() is also a cycle.
is also a cycle.
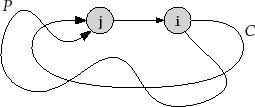
|
opendatastructures.org