Next: 12.3 Graph Traversal Up: 12. Graphs Previous: 12.1 : Representing a Contents
Adjacency list representations takes a more vertex-centric
approach. There are many different possible implementations of
adjacency lists. In this section, we present a simple one. At the end
of the section, we discuss different possibilities. In an adjacency
list representation, the graph ![]() is represented as an array,
is represented as an array,
![]() , of lists. The list
, of lists. The list
![]() contains a list of all the vertices
adjacent to vertex
contains a list of all the vertices
adjacent to vertex
![]() . That is, it contains every index
. That is, it contains every index
![]() such that
such that
![]() .
.
int n; List *adj;(An example is shown in Figure 12.3.) In this particular implementation, we represent each list in
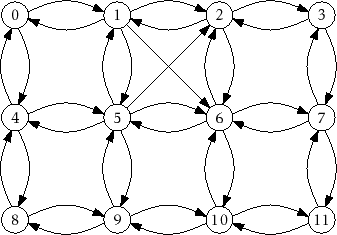
|
The
![]() operation just appends the value
operation just appends the value
![]() to the list
to the list
![]() :
:
void addEdge(int i, int j) {
adj[i].add(j);
}
This takes constant time.
The
![]() operation searches through the list
operation searches through the list
![]() until it finds
until it finds
![]() and then removes it:
and then removes it:
void removeEdge(int i, int j) {
for (int k = 0; k < adj[i].size(); k++) {
if (adj[i].get(k) == j) {
adj[i].remove(k);
return;
}
}
}
This takes
The
![]() operation is similar; it searches through the list
operation is similar; it searches through the list
![]() until it finds
until it finds
![]() (and returns true), or reaches the end of
the list (and returns false):
(and returns true), or reaches the end of
the list (and returns false):
bool hasEdge(int i, int j) {
return adj[i].contains(j);
}
This also takes
The
![]() operation is very simple; It simply copies the values in
operation is very simple; It simply copies the values in
![]() into the output list:
into the output list:
void outEdges(int i, LisT &edges) {
for (int k = 0; k < adj[i].size(); k++)
edges.add(adj[i].get(k));
}
This clearly takes
The
![]() operation is much more work. It scans over every
vertex
operation is much more work. It scans over every
vertex ![]() checking if the edge
checking if the edge
![]() exists and, if so, adding
exists and, if so, adding
![]() to the output list:
to the output list:
void inEdges(int i, LisT &edges) {
for (int j = 0; j < n; j++)
if (adj[j].contains(i)) edges.add(j);
}
This operation is very slow. It scans the adjacency list of every vertex,
so it takes
The following theorem summarizes the performance of the above data structure:
As alluded to earlier, there are many different choices to be made when implementing a graph as an adjacency list. Some questions that come up include:
opendatastructures.org