4.4 Analysis of Skiplists
In this section, we analyze the expected height, size, and length of
the search path in a skiplist. This section requires a background in
basic probability. Several proofs are based on the following basic
observation about coin tosses.
Lemma 4..2
Let 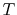 be the number of times a fair coin is tossed up to and including
the first time the coin comes up heads. Then
be the number of times a fair coin is tossed up to and including
the first time the coin comes up heads. Then
![$ \mathrm{E}[T]=2$](img548.png) .
.
Proof.
Suppose we stop tossing the coin the first time it comes up
heads. Define the indicator variable
Note that
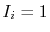
if and only if the first
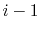
coin tosses are tails,
so
![$ \mathrm{E}[I_i]=\Pr\{I_i=1\}=1/2^{i-1}$](img552.png)
. Observe that
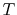
, the total
number of coin tosses, can be written as
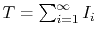
.
Therefore,

The next two lemmata tell us that skiplists have linear size:
Lemma 4..3
The expected number of nodes in a skiplist containing
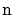 elements,
not including occurrences of the sentinel, is
elements,
not including occurrences of the sentinel, is
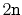 .
.
Proof.
The probability that any particular element,
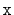
, is included in list
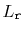
is
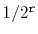
, so the expected number of nodes in
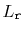
is
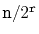
. Therefore, the total number of nodes in all lists is

Lemma 4..4
The expected height of a skiplist containing
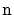 elements is at most
elements is at most
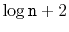 .
.
Proof.
For each
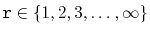
,
define the indicator random variable
The height,
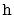
, of the skiplist is then given by
Note that
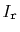
is never more than the length,
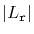
, of
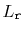
, so
Therefore, we have

Lemma 4..5
The expected number of nodes in a skiplist containing
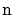 elements,
including all occurrences of the sentinel, is
elements,
including all occurrences of the sentinel, is
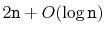 .
.
Proof.
By Lemma
4.3, the expected number of nodes, not
including the sentinel, is
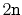
. The number of occurrences of
the sentinel is equal to the height,
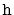
, of the skiplist so, by
Lemma
4.4 the expected number of occurrences of the
sentinel is at most
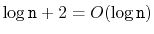
.

Lemma 4..6
The expected length of a search path in a skiplist is at most
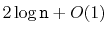 .
.
Proof.
The easiest way to see this is to consider the
reverse search
path for a node,
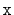
. This path starts at the predecessor of
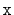
in
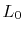
. At any point in time, if the path can go up a level, then
it does. If it cannot go up a level then it goes left. Observe that
the reverse search path for
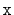
is identical to the search path for
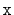
,
except that it is reversed.
The number of nodes that the reverse search path visits at a particular
level,
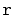 , is related to the following experiment: Toss a coin.
If the coin comes up heads then go up and stop, otherwise go left and
repeat the experiment. The number of coin tosses before the heads then
represents the number of steps to the left that a reverse search path
takes at a particular level.2 Lemma 4.2 tells us that the expected number
of coin tosses before the first heads is 1.
, is related to the following experiment: Toss a coin.
If the coin comes up heads then go up and stop, otherwise go left and
repeat the experiment. The number of coin tosses before the heads then
represents the number of steps to the left that a reverse search path
takes at a particular level.2 Lemma 4.2 tells us that the expected number
of coin tosses before the first heads is 1.
Let
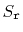 denote the number of steps the forward search path takes at level
denote the number of steps the forward search path takes at level
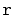 that go to the right. We have just argued that
that go to the right. We have just argued that
![$ \mathrm{E}[S_{\ensuremath{\mathtt{r}}}]\le
1$](img585.png) . Furthermore,
. Furthermore,
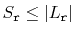 , since we can't take more steps
in
, since we can't take more steps
in
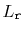 than the length of
than the length of
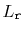 , so
, so
We can now finish as in the proof of Lemma
4.4.
Let
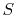
be the length of the search path for some node,
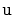
, in a
skiplist, and let
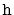
be the height of the skiplist. Then

The following theorem summarizes the results in this section:
Theorem 4..3
A skiplist containing
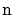 elements has expected size
elements has expected size
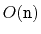 and the
expected length of the search path for any particular element is at most
and the
expected length of the search path for any particular element is at most
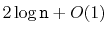 .
.
Footnotes
- ... level.2
- Note that this might overcount
the number of steps to the left, since the experiment should end either at
the first heads or when the search path reaches the sentinel, whichever
comes first. This is not a problem since the lemma is only stating an
upper bound.
opendatastructures.org

![$\displaystyle = \mathrm{E}\left[\sum_{i=1}^\infty I_i\right]$](img555.png)
![$\displaystyle = \sum_{i=1}^\infty \mathrm{E}\left[I_i\right]$](img556.png)
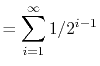
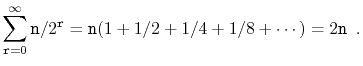
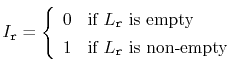
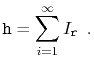
![$\displaystyle = \mathrm{E}\left[\sum_{r=1}^\infty I_{\ensuremath{\mathtt{r}}}\right]$](img573.png)
![$\displaystyle = \sum_{\ensuremath{\mathtt{r}}=1}^{\infty} E[I_{\ensuremath{\mathtt{r}}}]$](img574.png)
![$\displaystyle = \sum_{\ensuremath{\mathtt{r}}=1}^{\lfloor\log \ensuremath{\math...
...r\log \ensuremath{\mathtt{n}}\rfloor+1}^{\infty} E[I_{\ensuremath{\mathtt{r}}}]$](img575.png)
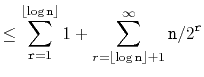
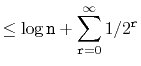
![]() , is related to the following experiment: Toss a coin.
If the coin comes up heads then go up and stop, otherwise go left and
repeat the experiment. The number of coin tosses before the heads then
represents the number of steps to the left that a reverse search path
takes at a particular level.2 Lemma 4.2 tells us that the expected number
of coin tosses before the first heads is 1.
, is related to the following experiment: Toss a coin.
If the coin comes up heads then go up and stop, otherwise go left and
repeat the experiment. The number of coin tosses before the heads then
represents the number of steps to the left that a reverse search path
takes at a particular level.2 Lemma 4.2 tells us that the expected number
of coin tosses before the first heads is 1.
![]() denote the number of steps the forward search path takes at level
denote the number of steps the forward search path takes at level
![]() that go to the right. We have just argued that
that go to the right. We have just argued that
![]() . Furthermore,
. Furthermore,
![]() , since we can't take more steps
in
, since we can't take more steps
in
![]() than the length of
than the length of
![]() , so
, so
![$\displaystyle = \mathrm{E}\left[ \ensuremath{\mathtt{h}} + \sum_{\ensuremath{\mathtt{r}}=0}^\infty S_{\ensuremath{\mathtt{r}}} \right]$](img590.png)
![$\displaystyle = \mathrm{E}[\ensuremath{\mathtt{h}}] + \sum_{\ensuremath{\mathtt{r}}=0}^\infty \mathrm{E}[S_{\ensuremath{\mathtt{r}}}]$](img591.png)
![$\displaystyle = \mathrm{E}[\ensuremath{\mathtt{h}}] + \sum_{\ensuremath{\mathtt...
...ensuremath{\mathtt{n}}\rfloor+1}^\infty \mathrm{E}[S_{\ensuremath{\mathtt{r}}}]$](img592.png)
![$\displaystyle \le \mathrm{E}[\ensuremath{\mathtt{h}}] + \sum_{\ensuremath{\math...
...mathtt{n}}\rfloor+1}^\infty \ensuremath{\mathtt{n}}/2^{\ensuremath{\mathtt{r}}}$](img593.png)
![$\displaystyle \le \mathrm{E}[\ensuremath{\mathtt{h}}] + \sum_{\ensuremath{\math...
...or} 1 + \sum_{\ensuremath{\mathtt{r}}=0}^{\infty} 1/2^{\ensuremath{\mathtt{r}}}$](img594.png)
![$\displaystyle \le \mathrm{E}[\ensuremath{\mathtt{h}}] + \sum_{\ensuremath{\math...
...or} 1 + \sum_{\ensuremath{\mathtt{r}}=0}^{\infty} 1/2^{\ensuremath{\mathtt{r}}}$](img594.png)