4.5 Discussion and Exercises

Skiplists were introduced by Pugh [52] who also presented a number of applications of skiplists [51]. Since then they have been studied extensively. Several researchers have done very precise analysis of the expected length and variance in length of the search path for the 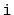$\mathtt{i}$th element in a skiplist [38,37,49]. Deterministic versions [44], biased versions [6,21], and self-adjusting versions [9] of skiplists have all been developed. Skiplist implementations have been written for various languages and frameworks and have seen use in open-source database systems [60,54]. A variant of skiplists is used in the HP-UX operating system kernel's process management structures [36]. Skiplists are even part of the Java 1.6 API [46].

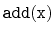
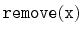
Exercise 4..1   Show that, during an $\mathtt{add(x)}$ or a $\mathtt{remove(x)}$ operation, the expected number of pointers in the structure that get changed is constant.

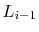
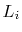
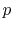
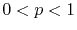
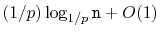
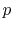
Exercise 4..2   Suppose that, instead of promoting an element from $L_{i-1}$ into $L_i$ based on a coin toss, we promote it with some probability $p$, $0 < p < 1$. Show that the expected length of the search path in this case is at most $(1/p)\log_{1/p} \ensuremath{\mathtt{n}} + O(1)$. What is the value of $p$ that minimizes this expression? What is the expected height of the skiplist? What is the expected number of nodes in the skiplist?

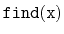
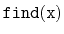
Exercise 4..3   Design and implement a $\mathtt{find(x)}$ method for SkiplistSSet that avoids locally-redundant comparisons; these are comparisons that have already been done and occur because $\ensuremath{\mathtt{u.next[r]}} = \ensuremath{\mathtt{u.next[r-1]}}$. Analyze the expected number of comparisons done by your modified $\mathtt{find(x)}$ method.

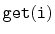
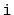
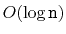
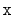
Exercise 4..4   Design and implement a version of a skiplist that implements the SSet interface, but also allows fast access to elements by rank. That is, it also supports the function $\mathtt{get(i)}$, which returns the element whose rank is $\mathtt{i}$ in $O(\log \ensuremath{\mathtt{n}})$ expected time. (The rank of an element $\mathtt{x}$ in an SSet is the number of elements in the SSet that are less than $\mathtt{x}$.)

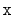
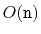
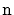
Exercise 4..5   Using the ideas from the space-efficient linked-list, SEList, design and implement a space-efficient SSet, SESSet. Do this by storing the data, in order, in an SEList and then storing the blocks of this SEList in an SSet. 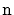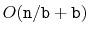If the original SSet implementation uses $O(\ensuremath{\mathtt{n}})$ space to store $\mathtt{n}$ elements, then the SESSet will use enough space for $\mathtt{n}$ elements plus $O(\ensuremath{\mathtt{n}}/\ensuremath{\mathtt{b}}+\ensuremath{\mathtt{b}})$ wasted space.

Exercise 4..6   Using an SSet as your underlying structure, design and implement an application that reads a (large) text file and allow you to search, interactively, for any substring contained in the text.

Hint 1: Every substring is a prefix of some suffix, so it suffices to store all suffixes of the text file.

Hint 2: Any suffix can be represented compactly as a single integer indicating where the suffix begins in the text.

Test your application on some large texts like some of the books available at Project Gutenberg [1].