Next: 6.2 : An Unbalanced Up: 6. Binary Trees Previous: 6. Binary Trees Contents
The simplest way to represent a node,
![]() , in a binary tree is
to store the (at most three) neighbours of
, in a binary tree is
to store the (at most three) neighbours of
![]() explicitly:
explicitly:
class BTNode {
N *left;
N *right;
N *parent;
BTNode() {
left = right = parent = NULL;
}
};
When one of these three neighbours is not present, we set it to
The binary tree itself can then be represented by a
pointer to its root node,
![]() :
:
Node *r; // root node
We can compute the depth of a node,
![]() , in a binary tree by counting
the number of steps on the path from
, in a binary tree by counting
the number of steps on the path from
![]() to the root:
to the root:
int depth(Node *u) {
int d = 0;
while (u != r) {
u = u->parent;
d++;
}
return d;
}
It is very easy to compute facts about binary trees using recursive algorithms. For example, to compute the size of (number of nodes in)
a binary tree rooted at node
![]() , we recursively compute the sizes of
the two subtrees rooted at the children of
, we recursively compute the sizes of
the two subtrees rooted at the children of
![]() , sum these sizes, and add one:
, sum these sizes, and add one:
int size(Node *u) {
if (u == nil) return 0;
return 1 + size(u->left) + size(u->right);
}
To compute the height of a node
![]() we can compute the height of
we can compute the height of
![]() 's
two subtrees, take the maximum, and add one:
's
two subtrees, take the maximum, and add one:
int height(Node *u) {
if (u == nil) return -1;
return 1 + max(height(u->left), height(u->right));
}
The two algorithms from the previous section use recursion to visit all the nodes in a binary tree. Each of them visits the nodes of the binary tree in the same order as the following code:
void traverse(Node *u) {
if (u == nil) return;
traverse(u->left);
traverse(u->right);
}
Using recursion this way produces very short, simple code, but can be problematic. The maximum depth of the recursion is given by the maximum depth of a node in the binary tree, i.e., the tree's height. If the height of the tree is very large, then this could very well use more stack space than is available, causing a crash.
Luckily, traversing a binary tree can be done without recursion. This
is done using an algorithm that uses where it came from
to decide where it will go next. See Figure 6.3.
If we arrive at a node
![]() from
from
![]() , then the next thing to do
is to visit
, then the next thing to do
is to visit
![]() . If we arrive at
. If we arrive at
![]() from
from
![]() , then the next
thing to do is to visit
, then the next
thing to do is to visit
![]() . If we arrive at
. If we arrive at
![]() from
from
![]() ,
then we are done visiting
,
then we are done visiting
![]() 's subtree, so we return to
's subtree, so we return to
![]() .
The following code implements this idea, with code included for handling
the cases where any of
.
The following code implements this idea, with code included for handling
the cases where any of
![]() ,
,
![]() , or
, or
![]() is
is
![]() :
:
void traverse2() {
Node *u = r, *prev = nil, *next;
while (u != nil) {
if (prev == u->parent) {
if (u->left != nil) next = u->left;
else if (u->right != nil) next = u->right;
else next = u->parent;
} else if (prev == u->left) {
if (u->right != nil) next = u->right;
else next = u->parent;
} else {
next = u->parent;
}
prev = u;
u = next;
}
}
|
The same things that can be computed with recursive algorithms can
also be done this way. For example, to compute the size of the tree we
keep a counter,
![]() , and increment
, and increment
![]() whenever visiting a node for the
first time:
whenever visiting a node for the
first time:
int size2() {
Node *u = r, *prev = nil, *next;
int n = 0;
while (u != nil) {
if (prev == u->parent) {
n++;
if (u->left != nil) next = u->left;
else if (u->right != nil) next = u->right;
else next = u->parent;
} else if (prev == u->left) {
if (u->right != nil) next = u->right;
else next = u->parent;
} else {
next = u->parent;
}
prev = u;
u = next;
}
return n;
}
In some implementations of binary trees, the
![]() field is not used.
When this is the case, a non-recursive implementation is still possible,
but the implementation has to use a
field is not used.
When this is the case, a non-recursive implementation is still possible,
but the implementation has to use a
![]() (or
(or
![]() ) to keep track
of the path from the current node to the root.
) to keep track
of the path from the current node to the root.
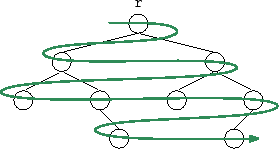
A special kind of traversal that does not fit the pattern of the above
functions is the breadth-first traversal. In a breadth-first
traversal, the nodes are visited level-by-level starting at the root
and working our way down, visiting the nodes at each level from left
to right. This is similar to the way we would read a page of English
text. (See Figure 6.4.) This is implemented using a queue,
![]() ,
that initially contains only the root,
,
that initially contains only the root,
![]() . At each step, we extract
the next node,
. At each step, we extract
the next node,
![]() , from
, from
![]() , process
, process
![]() and add
and add
![]() and
and
![]() (if they are non-
(if they are non-
![]() ) to
) to
![]() :
:
void bfTraverse() {
ArrayDeque<Node*> q;
if (r != nil) q.add(q.size(),r);
while (q.size() > 0) {
Node *u = q.remove(q.size()-1);
if (u->left != nil) q.add(q.size(),u->left);
if (u->right != nil) q.add(q.size(),u->right);
}
}
|
opendatastructures.org