Next: 4.3 SkiplistList: An Efficient Up: 4. Skiplists Previous: 4.1 The Basic Structure Contents Index
A SkiplistSSet uses a skiplist structure to implement the SSet
interface. When used in this way, the list ![]() stores the elements of
the SSet in sorted order. The
stores the elements of
the SSet in sorted order. The
![]() method works by following
the search path for the smallest value
method works by following
the search path for the smallest value
![]() such that
such that
![]() :
:
![\begin{leftbar}
\begin{flushleft}
\hspace*{1em} \ensuremath{\mathrm{find\_pred\_...
...emath{\mathit{next}}[0].\ensuremath{\mathit{x}}}\\
\end{flushleft}\end{leftbar}](img1625.png)
Following the search path for
![]() is easy: when situated at
some node,
is easy: when situated at
some node,
![]() , in
, in
![]() , we look right to
, we look right to
![]() .
If
.
If
![]() , then we take a step to the right in
, then we take a step to the right in
![]() ; otherwise, we move down into
; otherwise, we move down into
![]() . Each step
(right or down) in this search takes only constant time; thus, by
Lemma 4.1, the expected running time of
. Each step
(right or down) in this search takes only constant time; thus, by
Lemma 4.1, the expected running time of
![]() is
is
![]() .
.
Before we can add an element to a SkipListSSet, we need a method to
simulate tossing coins to determine the height,
![]() , of a new node.
We do so by picking a random integer,
, of a new node.
We do so by picking a random integer,
![]() , and counting the number of
trailing
, and counting the number of
trailing ![]() s in the binary representation of
s in the binary representation of
![]() :4.1
:4.1
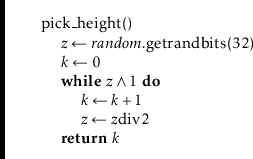
To implement the
![]() method in a SkiplistSSet we search for
method in a SkiplistSSet we search for
![]() and then splice
and then splice
![]() into a few lists
into a few lists ![]() ,...,
,...,
![]() , where
, where
![]() is selected using the
is selected using the
![]() method. The easiest way to do this
is to use an array,
method. The easiest way to do this
is to use an array,
![]() , that keeps track of the nodes at which
the search path goes down from some list
, that keeps track of the nodes at which
the search path goes down from some list
![]() into
into
![]() .
More precisely,
.
More precisely,
![]() is the node in
is the node in
![]() where the search path
proceeded down into
where the search path
proceeded down into
![]() . The nodes that we modify to insert
. The nodes that we modify to insert
![]() are precisely the nodes
are precisely the nodes
![]() . The following
code implements this algorithm for
. The following
code implements this algorithm for
![]() :
:

Removing an element,
![]() , is done in a similar way, except that there
is no need for
, is done in a similar way, except that there
is no need for
![]() to keep track of the search path. The removal
can be done as we are following the search path. We search for
to keep track of the search path. The removal
can be done as we are following the search path. We search for
![]() and each time the search moves downward from a node
and each time the search moves downward from a node
![]() , we check if
, we check if
![]() and if so, we splice
and if so, we splice
![]() out of the list:
out of the list:

The following theorem summarizes the performance of skiplists when used to implement sorted sets: