Next: 10.2 MeldableHeap: A Randomized Up: 10. Heaps Previous: 10. Heaps Contents Index
Our first implementation of a (priority) Queue is based on a technique that is over four hundred years old. Eytzinger's method allows us to represent a complete binary tree as an array by laying out the nodes of the tree in breadth-first order (see Section 6.1.2). In this way, the root is stored at position 0, the root's left child is stored at position 1, the root's right child at position 2, the left child of the left child of the root is stored at position 3, and so on. See Figure 10.1.
If we apply Eytzinger's method to a sufficiently large tree, some
patterns emerge. The left child of the node at index
![]() is at index
is at index
![]() and the right child of the node at index
and the right child of the node at index
![]() is at
index
is at
index
![]() . The parent of the node at index
. The parent of the node at index
![]() is at
index
is at
index
![]() .
.

A BinaryHeap uses this technique to implicitly represent a complete
binary tree in which the elements are heap-ordered:
The value
stored at any index
![]() is not smaller than the value stored at index
is not smaller than the value stored at index
![]() , with the exception of the root value,
, with the exception of the root value,
![]() . It follows
that the smallest value in the priority Queue is therefore stored at
position 0 (the root).
. It follows
that the smallest value in the priority Queue is therefore stored at
position 0 (the root).
In a BinaryHeap, the
![]() elements are stored in an array
elements are stored in an array
![]() :
:
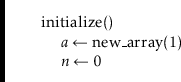
Implementing the
![]() operation is fairly straightforward. As with
all array-based structures, we first check to see if
operation is fairly straightforward. As with
all array-based structures, we first check to see if
![]() is full (by checking if
is full (by checking if
![]() ) and, if so, we grow
) and, if so, we grow
![]() . Next, we place
. Next, we place
![]() at location
at location
![]() and increment
and increment
![]() . At this point, all that remains is to ensure
that we maintain the heap property. We do this by repeatedly swapping
. At this point, all that remains is to ensure
that we maintain the heap property. We do this by repeatedly swapping
![]() with its parent until
with its parent until
![]() is no longer smaller than its parent.
See Figure 10.2.
is no longer smaller than its parent.
See Figure 10.2.

Implementing the
![]() operation, which removes the smallest value
from the heap, is a little trickier. We know where the smallest value is
(at the root), but we need to replace it after we remove it and ensure
that we maintain the heap property.
operation, which removes the smallest value
from the heap, is a little trickier. We know where the smallest value is
(at the root), but we need to replace it after we remove it and ensure
that we maintain the heap property.
The easiest way to do this is to replace the root with the value
![]() , delete
that value, and decrement
, delete
that value, and decrement
![]() . Unfortunately, the new root element is now
probably not the smallest element, so it needs to be moved downwards.
We do this by repeatedly comparing this element to its two children.
If it is the smallest of the three then we are done. Otherwise, we swap
this element with the smallest of its two children and continue.
. Unfortunately, the new root element is now
probably not the smallest element, so it needs to be moved downwards.
We do this by repeatedly comparing this element to its two children.
If it is the smallest of the three then we are done. Otherwise, we swap
this element with the smallest of its two children and continue.

As with other array-based structures, we will ignore the time spent in
calls to
![]() , since these can be accounted for using the amortization
argument from Lemma 2.1. The running times of
both
, since these can be accounted for using the amortization
argument from Lemma 2.1. The running times of
both
![]() and
and
![]() then depend on the height of the (implicit)
binary tree. Luckily, this is a complete
binary tree; every level
except the last has the maximum possible number of nodes. Therefore,
if the height of this tree is
then depend on the height of the (implicit)
binary tree. Luckily, this is a complete
binary tree; every level
except the last has the maximum possible number of nodes. Therefore,
if the height of this tree is ![]() , then it has at least
, then it has at least ![]() nodes.
Stated another way
nodes.
Stated another way
The following theorem summarizes the performance of a BinaryHeap:
Furthermore, beginning with an empty BinaryHeap, any sequence of ![]()
![]() and
and
![]() operations results in a total of
operations results in a total of ![]() time spent during all calls to
time spent during all calls to
![]() .
.
opendatastructures.org