Subsections

1.2 Interfaces

When discussing data structures, it is important to understand the difference between a data structure's interface and its implementation. An interface describes what a data structure does, while an implementation describes how the data structure does it.

An interface, sometimes also called an abstract data type, defines the set of operations supported by a data structure and the semantics, or meaning, of those operations. An interface tells us nothing about how the data structure implements these operations; it only provides a list of supported operations along with specifications about what types of arguments each operation accepts and the value returned by each operation.

A data structure implementation, on the other hand, includes the internal representation of the data structure as well as the definitions of the algorithms that implement the operations supported by the data structure. Thus, there can be many implementations of a single interface. For example, in Chapter 2, we will see implementations of the $\mathtt{List}$ interface using arrays and in Chapter 3 we will see implementations of the $\mathtt{List}$ interface using pointer-based data structures. Each implements the same interface, $\mathtt{List}$ , but in different ways.

1.2.1 The $\mathtt{Queue}$ , $\mathtt{Stack}$ , and $\mathtt{Deque}$ Interfaces

The $\mathtt{Queue}$ interface represents a collection of elements to which we can add elements and remove the next element. More precisely, the operations supported by the $\mathtt{Queue}$ interface are

$\mathtt{add(x)}$ : add the value $\mathtt{x}$ to the $\mathtt{Queue}$
$\mathtt{remove()}$ : remove the next (previously added) value, $\mathtt{y}$ , from the $\mathtt{Queue}$ and return $\mathtt{y}$

Notice that the $\mathtt{remove()}$ operation takes no argument. The $\mathtt{Queue}$ 's queueing discipline decides which element should be removed. There are many possible queueing disciplines, the most common of which include FIFO, priority, and LIFO.

A FIFO (first-in-first-out) $\mathtt{Queue}$ , which is illustrated in Figure 1.1, removes items in the same order they were added, much in the same way a queue (or line-up) works when checking out at a cash register in a grocery store. This is the most common kind of $\mathtt{Queue}$ so the qualifier FIFO is often omitted. In other texts, the $\mathtt{add(x)}$ and $\mathtt{remove()}$ operations on a FIFO $\mathtt{Queue}$ are often called $\mathtt{enqueue(x)}$ and $\mathtt{dequeue()}$ , respectively.

**Figure 1.1:** A FIFO $\mathtt{Queue}$ .
$\includegraphics[width=\textwidth ]{figs/queue}$

A priority $\mathtt{Queue}$ , illustrated in Figure 1.2, always removes the smallest element from the $\mathtt{Queue}$ , breaking ties arbitrarily. This is similar to the way in which patients are triaged in a hospital emergency room. As patients arrive they are evaluated and then placed in a waiting room. When a doctor becomes available he or she first treats the patient with the most life-threatening condition. The $\mathtt{remove(x)}$ operation on a priority $\mathtt{Queue}$ is usually called $\mathtt{deleteMin()}$ in other texts.

**Figure 1.2:** A priority $\mathtt{Queue}$ .
$\includegraphics[width=\textwidth ]{figs/prioqueue}$

A very common queueing discipline is the LIFO (last-in-first-out) discipline, illustrated in Figure 1.3. In a LIFO Queue, the most recently added element is the next one removed. This is best visualized in terms of a stack of plates; plates are placed on the top of the stack and also removed from the top of the stack. This structure is so common that it gets its own name: $\mathtt{Stack}$ . Often, when discussing a $\mathtt{Stack}$ , the names of $\mathtt{add(x)}$ and $\mathtt{remove()}$ are changed to $\mathtt{push(x)}$ and $\mathtt{pop()}$ ; this is to avoid confusing the LIFO and FIFO queueing disciplines.

**Figure 1.3:** A stack.
$\includegraphics[width=\textwidth ]{figs/stack}$

A $\mathtt{Deque}$ is a generalization of both the FIFO $\mathtt{Queue}$ and LIFO $\mathtt{Queue}$ ( $\mathtt{Stack}$ ). A $\mathtt{Deque}$ represents a sequence of elements, with a front and a back. Elements can be added at the front of the sequence or the back of the sequence. The names of the $\mathtt{Deque}$ operations are self-explanatory: $\mathtt{addFirst(x)}$ , $\mathtt{removeFirst()}$ , $\mathtt{addLast(x)}$ , and $\mathtt{removeLast()}$ . It is worth noting that a $\mathtt{Stack}$ can be implemented using only $\mathtt{addFirst(x)}$ and $\mathtt{removeFirst()}$ while a FIFO $\mathtt{Queue}$ can be implemented using $\mathtt{addLast(x)}$ and $\mathtt{removeFirst()}$ .

1.2.2 The $\mathtt{List}$ Interface: Linear Sequences

This book will talk very little about the FIFO $\mathtt{Queue}$ , $\mathtt{Stack}$ , or $\mathtt{Deque}$ interfaces. This is because these interfaces are subsumed by the $\mathtt{List}$ interface. A $\mathtt{List}$ , illustrated in Figure 1.4, represents a sequence, $\ensuremath{\mathtt{x}}_0,\ldots,\ensuremath{\mathtt{x}}_{\ensuremath{\mathtt{n}}-1}$ , of values. The $\mathtt{List}$ interface includes the following operations:

$\mathtt{size()}$ : return $\mathtt{n}$ , the length of the list
$\mathtt{get(i)}$ : return the value $\ensuremath{\mathtt{x}}_{\ensuremath{\mathtt{i}}}$
$\mathtt{set(i,x)}$ : set the value of $\ensuremath{\mathtt{x}}_{\ensuremath{\mathtt{i}}}$ equal to $\mathtt{x}$
$\mathtt{add(i,x)}$ : add $\mathtt{x}$ at position $\mathtt{i}$ , displacing $\ensuremath{\mathtt{x}}_{\ensuremath{\mathtt{i}}},\ldots,\ensuremath{\mathtt{x}}_{\ensuremath{\mathtt{n}}-1}$ ;
Set $\ensuremath{\mathtt{x}}_{j+1}=\ensuremath{\mathtt{x}}_j$ , for all $j\in\{\ensuremath{\mathtt{n}}-1,\ldots,\ensuremath{\mathtt{i}}\}$ , increment $\mathtt{n}$ , and set $\ensuremath{\mathtt{x}}_i=\ensuremath{\mathtt{x}}$
$\mathtt{remove(i)}$ remove the value $\ensuremath{\mathtt{x}}_{\ensuremath{\mathtt{i}}}$ , displacing $\ensuremath{\mathtt{x}}_{\ensuremath{\mathtt{i+1}}},\ldots,\ensuremath{\mathtt{x}}_{\ensuremath{\mathtt{n}}-1}$ ;
Set $\ensuremath{\mathtt{x}}_{j}=\ensuremath{\mathtt{x}}_{j+1}$ , for all $j\in\{\ensuremath{\mathtt{i}},\ldots,\ensuremath{\mathtt{n}}-2\}$ and decrement $\mathtt{n}$

Notice that these operations are easily sufficient to implement the $\mathtt{Deque}$ interface:

$\displaystyle \ensuremath{\mathtt{addFirst(x)}}$	$\displaystyle \Rightarrow$	$\displaystyle \ensuremath{\mathtt{add(0,x)}}$
$\displaystyle \ensuremath{\mathtt{removeFirst()}}$	$\displaystyle \Rightarrow$	$\displaystyle \ensuremath{\mathtt{remove(0)}}$
$\displaystyle \ensuremath{\mathtt{addLast(x)}}$	$\displaystyle \Rightarrow$	$\displaystyle \ensuremath{\mathtt{add(size(),x)}}$
$\displaystyle \ensuremath{\mathtt{removeLast()}}$	$\displaystyle \Rightarrow$	$\displaystyle \ensuremath{\mathtt{remove(size()-1)}}$

**Figure 1.4:** A $\mathtt{List}$ represents a sequence indexed by $0,1,2,\ldots,\ensuremath{\mathtt{n}}-1$ . In this $\mathtt{List}$ a call to $\mathtt{get(2)}$ would return the value .
$\includegraphics[width=\textwidth ]{figs/list}$

Although we will normally not discuss the $\mathtt{Stack}$ , $\mathtt{Deque}$ and FIFO $\mathtt{Queue}$ interfaces in subsequent chapters, the terms $\mathtt{Stack}$ and $\mathtt{Deque}$ are sometimes used in the names of data structures that implement the $\mathtt{List}$ interface. When this happens, it highlights the fact that these data structures can be used to implement the $\mathtt{Stack}$ or $\mathtt{Deque}$ interface very efficiently. For example, the $\mathtt{ArrayDeque}$ class is an implementation of the $\mathtt{List}$ interface that implements all the $\mathtt{Deque}$ operations in constant time per operation.

1.2.3 The $\mathtt{USet}$ Interface: Unordered Sets

The $\mathtt{USet}$ interface represents an unordered set of unique elements, which mimics a mathematical set. A $\mathtt{USet}$ contains $\mathtt{n}$ distinct elements; no element appears more than once; the elements are in no specific order. A $\mathtt{USet}$ supports the following operations:

$\mathtt{size()}$ : return the number, $\mathtt{n}$ , of elements in the set
$\mathtt{add(x)}$ : add the element $\mathtt{x}$ to the set if not already present;
Add $\mathtt{x}$ to the set provided that there is no element $\mathtt{y}$ in the set such that $\mathtt{x}$ equals $\mathtt{y}$ . Return $\mathtt{true}$ if $\mathtt{x}$ was added to the set and $\mathtt{false}$ otherwise.
$\mathtt{remove(x)}$ : remove $\mathtt{x}$ from the set;
Find an element $\mathtt{y}$ in the set such that $\mathtt{x}$ equals $\mathtt{y}$ and remove $\mathtt{y}$ . Return $\mathtt{y}$ , or $\mathtt{null}$ if no such element exists.
$\mathtt{find(x)}$ : find $\mathtt{x}$ in the set if it exists;
Find an element $\mathtt{y}$ in the set such that $\mathtt{y}$ equals $\mathtt{x}$ . Return $\mathtt{y}$ , or $\mathtt{null}$ if no such element exists.

These definitions are a bit fussy about distinguishing $\mathtt{x}$ , the element we are removing or finding, from $\mathtt{y}$ , the element we may remove or find. This is because $\mathtt{x}$ and $\mathtt{y}$ might actually be distinct objects that are nevertheless treated as equal. Such a distinction is useful because it allows for the creation of dictionaries or maps that map keys onto values.

To create a dictionary/map, one forms compound objects called $\mathtt{Pair}$ s, each of which contains a key and a value. Two $\mathtt{Pair}$ s are treated as equal if their keys are equal. If we store some pair $(\ensuremath{\mathtt{k}},\ensuremath{\mathtt{v}})$ in a $\mathtt{USet}$ and then later call the $\mathtt{find(x)}$ method using the pair $\ensuremath{\mathtt{x}}=(\ensuremath{\mathtt{k}},\ensuremath{\mathtt{null}})$ the result will be $\ensuremath{\mathtt{y}}=(\ensuremath{\mathtt{k}},\ensuremath{\mathtt{v}})$ . In other words, it is possible to recover the value, $\mathtt{v}$ , given only the key, $\mathtt{k}$ .

1.2.4 The $\mathtt{SSet}$ Interface: Sorted Sets

The $\mathtt{SSet}$ interface represents a sorted set of elements. An $\mathtt{SSet}$ stores elements from some total order, so that any two elements $\mathtt{x}$ and $\mathtt{y}$ can be compared. In code examples, this will be done with a method called $\mathtt{compare(x,y)}$ in which

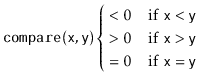
$\displaystyle \ensuremath{\mathtt{compare(x,y)}} \begin{cases} {}<0 & \text{... ...{}=0 & \text{if $\ensuremath{\mathtt{x}}=\ensuremath{\mathtt{y}}$} \end{cases}$

An $\mathtt{SSet}$ supports the $\mathtt{size()}$ , $\mathtt{add(x)}$ , and $\mathtt{remove(x)}$ methods with exactly the same semantics as in the $\mathtt{USet}$ interface. The difference between a $\mathtt{USet}$ and an $\mathtt{SSet}$ is in the $\mathtt{find(x)}$ method:

$\mathtt{find(x)}$ : locate $\mathtt{x}$ in the sorted set;
Find the smallest element $\mathtt{y}$ in the set such that $\ensuremath{\mathtt{y}} \ge \ensuremath{\mathtt{x}}$ . Return $\mathtt{y}$ or $\mathtt{null}$ if no such element exists.

This version of the $\mathtt{find(x)}$ operation is sometimes referred to as a successor search. It differs in a fundamental way from $\mathtt{USet.find(x)}$ since it returns a meaningful result even when there is no element equal to $\mathtt{x}$ in the set.

The distinction between the $\mathtt{USet}$ and $\mathtt{SSet}$ $\mathtt{find(x)}$ operations is very important and often missed. The extra functionality provided by an $\mathtt{SSet}$ usually comes with a price that includes both a larger running time and a higher implementation complexity. For example, most of the $\mathtt{SSet}$ implementations discussed in this book all have $\mathtt{find(x)}$ operations with running times that are logarithmic in the size of the set. On the other hand, the implementation of a $\mathtt{USet}$ as a $\mathtt{ChainedHashTable}$ in Chapter 5 has a $\mathtt{find(x)}$ operation that runs in constant expected time. When choosing which of these structures to use, one should always use a $\mathtt{USet}$ unless the extra functionality offered by an $\mathtt{SSet}$ is truly needed.