In the next section, we look at the operations supported by the most
commonly used data structures. Anyone with a bit of programming
experience will see that these operations are not hard to implement
correctly. We can store the data in an array or a linked list and each
operation can be implemented by iterating over all the elements of the
array or list and possibly adding or removing an element.
This kind of implementation is easy, but not very efficient. Does this
really matter? Computers are becoming faster and faster. Maybe the
obvious implementation is good enough. Let's do some rough calculations
to find out.
Imagine an application with a
moderately-sized data set, say of one million (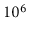 ), items. It is
reasonable, in most applications, to assume that the application will
want to look up each item at least once. This means we can expect to do
at least one million (
), items. It is
reasonable, in most applications, to assume that the application will
want to look up each item at least once. This means we can expect to do
at least one million (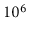 ) searches in this data. If each of these
) searches in this data. If each of these
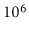 searches inspects each of the
searches inspects each of the 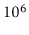 items, this gives a total
of
items, this gives a total
of
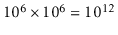 (one thousand billion) inspections.
(one thousand billion) inspections.
At the time of writing, even a very fast
desktop computer can not do more than one billion (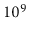 ) operations per
second.1.1This means that this application will take at least
) operations per
second.1.1This means that this application will take at least
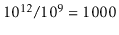 seconds, or roughly 16 minutes and 40 seconds. Sixteen minutes is an
eon in computer time, but a person might be willing to put up with it
(if he or she were headed out for a coffee break).
seconds, or roughly 16 minutes and 40 seconds. Sixteen minutes is an
eon in computer time, but a person might be willing to put up with it
(if he or she were headed out for a coffee break).
Now consider a company like Google,
that
indexes over 8.5 billion web pages. By our calculations, doing any kind
of query over this data would take at least 8.5 seconds. We already
know that this isn't the case; web searches complete in much less than
8.5 seconds, and they do much more complicated queries than just asking
if a particular page is in their list of indexed pages. At the time
of writing, Google receives approximately 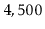 queries per second,
meaning that they would require at least
queries per second,
meaning that they would require at least
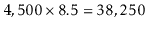 very
fast servers just to keep up.
very
fast servers just to keep up.
These examples tell us that the obvious implementations of data structures
do not scale well when the number of items,
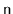 , in the data structure
and the number of operations,
, in the data structure
and the number of operations, 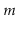 , performed on the data structure
are both large. In these cases, the time (measured in, say, machine
instructions) is roughly
, performed on the data structure
are both large. In these cases, the time (measured in, say, machine
instructions) is roughly
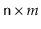 .
.
The solution, of course, is to carefully organize data within the data
structure so that not every operation requires every data item to be
inspected. Although it sounds impossible at first, we will see data
structures where a search requires looking at only two items on average,
independent of the number of items stored in the data structure. In our
billion instruction per second computer it takes only
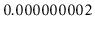 seconds to search in a data structure containing a billion items (or a
trillion, or a quadrillion, or even a quintillion items).
seconds to search in a data structure containing a billion items (or a
trillion, or a quadrillion, or even a quintillion items).
We will also see implementations of data structures that keep the
items in sorted order, where the number of items inspected during an
operation grows very slowly as a function of the number of items in
the data structure. For example, we can maintain a sorted set of one
billion items while inspecting at most 60 items during any operation.
In our billion instruction per second computer, these operations take
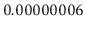 seconds each.
seconds each.
The remainder of this chapter briefly reviews some of the main concepts
used throughout the rest of the book. Section 1.2 describes
the interfaces implemented by all of the data structures described in
this book and should be considered required reading. The remaining
sections discuss:
- some mathematical review including exponentials, logarithms,
factorials, asymptotic (big-Oh) notation, probability, and randomization;
- the model of computation;
- correctness, running time, and space;
- an overview of the rest of the chapters; and
- the sample code and typesetting conventions.
A reader with or without a background in these areas can easily skip
them now and come back to them later if necessary.
Footnotes
- ...
second.1.1
- Computer speeds are at most a few gigahertz (billions
of cycles per second), and each operation typically takes a few cycles.
opendatastructures.org
![]() seconds to search in a data structure containing a billion items (or a
trillion, or a quadrillion, or even a quintillion items).
seconds to search in a data structure containing a billion items (or a
trillion, or a quadrillion, or even a quintillion items).
![]() seconds each.
seconds each.