4.2 SkiplistSSet: An Efficient SSet

A SkiplistSSet uses a skiplist structure to implement the SSet interface. When used in this way, the list $L_0$ stores the elements of the SSet in sorted order. The $\ensuremath{\mathrm{find}(\ensuremath{\mathit{x}})}$ method works by following the search path for the smallest value $\ensuremath{\ensuremath{\mathit{y}}}$ such that $\ensuremath{\ensuremath{\ensuremath{\mathit{y}}}}\ge\ensuremath{\ensuremath{\ensuremath{\mathit{x}}}}$:

Following the search path for $\ensuremath{\ensuremath{\mathit{y}}}$ is easy: when situated at some node, $\ensuremath{\ensuremath{\mathit{u}}}$, in $L_{\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}}}$, we look right to $\ensuremath{\ensuremath{\mathit{u}}.\ensuremath{\mathit{next}}[\ensuremath{\mathit{r}}].\ensuremath{\mathit{x}}}$. If $\ensuremath{\ensuremath{\ensuremath{\mathit{x}}}}>\ensuremath{\ensuremath{\ens... ...}.\ensuremath{\mathit{next}}[\ensuremath{\mathit{r}}].\ensuremath{\mathit{x}}}}$, then we take a step to the right in $L_{\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}}}$; otherwise, we move down into $L_{\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}}-1}$. Each step (right or down) in this search takes only constant time; thus, by Lemma 4.1, the expected running time of $\ensuremath{\mathrm{find}(\ensuremath{\mathit{x}})}$ is $O(\log \ensuremath{\ensuremath{\ensuremath{\mathit{n}}}})$.

Before we can add an element to a SkipListSSet, we need a method to simulate tossing coins to determine the height, $\ensuremath{\ensuremath{\mathit{k}}}$, of a new node. We do so by picking a random integer, $\ensuremath{\ensuremath{\mathit{z}}}$, and counting the number of trailing $1$s in the binary representation of $\ensuremath{\ensuremath{\mathit{z}}}$:^4.1

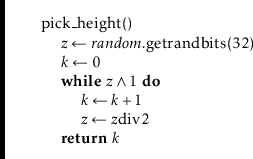
To implement the $\ensuremath{\mathrm{add}(\ensuremath{\mathit{x}})}$ method in a SkiplistSSet we search for $\ensuremath{\ensuremath{\mathit{x}}}$ and then splice $\ensuremath{\ensuremath{\mathit{x}}}$ into a few lists $L_0$,..., $L_{\ensuremath{\ensuremath{\ensuremath{\mathit{k}}}}}$, where $\ensuremath{\ensuremath{\mathit{k}}}$ is selected using the $\ensuremath{\mathrm{pick\_height}()}$ method. The easiest way to do this is to use an array, $\ensuremath{\ensuremath{\mathit{stack}}}$, that keeps track of the nodes at which the search path goes down from some list $L_{\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}}}$ into $L_{\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}}-1}$. More precisely, $\ensuremath{\ensuremath{\mathit{stack}}[\ensuremath{\mathit{r}}]}$ is the node in $L_{\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}}}$ where the search path proceeded down into $L_{\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}}-1}$. The nodes that we modify to insert $\ensuremath{\ensuremath{\mathit{x}}}$ are precisely the nodes $\ensuremath{\ensuremath{\ensuremath{\mathit{stack}}[0]}},\ldots,\ensuremath{\ensuremath{\ensuremath{\mathit{stack}}[\ensuremath{\mathit{k}}]}}$. The following code implements this algorithm for $\ensuremath{\mathrm{add}(\ensuremath{\mathit{x}})}$:

Figure 4.3: Adding the node containing $3.5$ to a skiplist. The nodes stored in $\ensuremath{\ensuremath{\mathit{stack}}}$ are highlighted.

Removing an element, $\ensuremath{\ensuremath{\mathit{x}}}$, is done in a similar way, except that there is no need for $\ensuremath{\ensuremath{\mathit{stack}}}$ to keep track of the search path. The removal can be done as we are following the search path. We search for $\ensuremath{\ensuremath{\mathit{x}}}$ and each time the search moves downward from a node $\ensuremath{\ensuremath{\mathit{u}}}$, we check if $\ensuremath{\ensuremath{\ensuremath{\mathit{u}}.\ensuremath{\mathit{next}}.\ensuremath{\mathit{x}}}}=\ensuremath{\ensuremath{\ensuremath{\mathit{x}}}}$ and if so, we splice $\ensuremath{\ensuremath{\mathit{u}}}$ out of the list:

Figure 4.4: Removing the node containing $3$ from a skiplist.

4.2.1 Summary

The following theorem summarizes the performance of skiplists when used to implement sorted sets:

Theorem 4..1   SkiplistSSet implements the SSet interface. A SkiplistSSet supports the operations $\ensuremath{\mathrm{add}(\ensuremath{\mathit{x}})}$, $\ensuremath{\mathrm{remove}(\ensuremath{\mathit{x}})}$, and $\ensuremath{\mathrm{find}(\ensuremath{\mathit{x}})}$ in $O(\log \ensuremath{\ensuremath{\ensuremath{\mathit{n}}}})$ expected time per operation.

Footnotes

...:^4.1

This method does not exactly replicate the coin-tossing experiment since the value of $\ensuremath{\ensuremath{\mathit{k}}}$ will always be less than the number of bits in an $\ensuremath{\ensuremath{\mathit{int}}}$. However, this will have negligible impact unless the number of elements in the structure is much greater than $2^{32}=4294967296$.