3.2 DLList: A Doubly-Linked List

A DLList (doubly-linked list) is very similar to an SLList except that each node $\ensuremath{\ensuremath{\mathit{u}}}$ in a DLList has references to both the node $\ensuremath{\ensuremath{\mathit{u}}.\ensuremath{\mathit{next}}}$ that follows it and the node $\ensuremath{\ensuremath{\mathit{u}}.\ensuremath{\mathit{prev}}}$ that precedes it.

When implementing an SLList, we saw that there were always several special cases to worry about. For example, removing the last element from an SLList or adding an element to an empty SLList requires care to ensure that $\ensuremath{\ensuremath{\mathit{head}}}$ and $\ensuremath{\ensuremath{\mathit{tail}}}$ are correctly updated. In a DLList, the number of these special cases increases considerably. Perhaps the cleanest way to take care of all these special cases in a DLList is to introduce a $\ensuremath{\ensuremath{\mathit{dummy}}}$ node. This is a node that does not contain any data, but acts as a placeholder so that there are no special nodes; every node has both a $\ensuremath{\ensuremath{\mathit{next}}}$ and a $\ensuremath{\ensuremath{\mathit{prev}}}$ , with $\ensuremath{\ensuremath{\mathit{dummy}}}$ acting as the node that follows the last node in the list and that precedes the first node in the list. In this way, the nodes of the list are (doubly-)linked into a cycle, as illustrated in Figure 3.2.

**Figure 3.2:** A DLList containing a,b,c,d,e.
$\includegraphics[width=\textwidth ]{figs-python/dllist2}$

$\begin{leftbar} \begin{flushleft} \hspace*{1em} \ensuremath{\mathrm{initialize}(... ...my}}.\ensuremath{next} \gets \ensuremath{dummy}}\\ \end{flushleft}\end{leftbar}$

Finding the node with a particular index in a DLList is easy; we can either start at the head of the list ( $\ensuremath{\ensuremath{\mathit{dummy}}.\ensuremath{\mathit{next}}}$ ) and work forward, or start at the tail of the list ( $\ensuremath{\ensuremath{\mathit{dummy}}.\ensuremath{\mathit{prev}}}$ ) and work backward. This allows us to reach the $\ensuremath{\ensuremath{\mathit{i}}}$ th node in $O(1+\min\{\ensuremath{\ensuremath{\ensuremath{\mathit{i}}}},\ensuremath{\ensur... ...{\ensuremath{\mathit{n}}}}-\ensuremath{\ensuremath{\ensuremath{\mathit{i}}}}\})$ time:

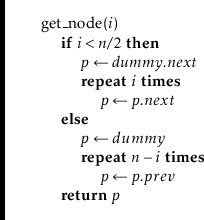
$\begin{leftbar} \begin{flushleft} \hspace*{1em} \ensuremath{\mathrm{get\_node}(\... ...bf{return}} \ensuremath{\ensuremath{\mathit{p}}}\\ \end{flushleft}\end{leftbar}$

The $\ensuremath{\mathrm{get}(\ensuremath{\mathit{i}})}$ and $\ensuremath{\mathrm{set}(\ensuremath{\mathit{i}},\ensuremath{\mathit{x}})}$ operations are now also easy. We first find the $\ensuremath{\ensuremath{\mathit{i}}}$ th node and then get or set its $\ensuremath{\ensuremath{\mathit{x}}}$ value:

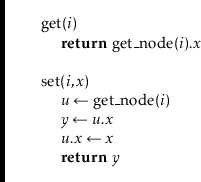
$\begin{leftbar} \begin{flushleft} \hspace*{1em} \ensuremath{\mathrm{get}(\ensure... ...bf{return}} \ensuremath{\ensuremath{\mathit{y}}}\\ \end{flushleft}\end{leftbar}$

The running time of these operations is dominated by the time it takes to find the $\ensuremath{\ensuremath{\mathit{i}}}$ th node, and is therefore $O(1+\min\{\ensuremath{\ensuremath{\ensuremath{\mathit{i}}}},\ensuremath{\ensur... ...{\ensuremath{\mathit{n}}}}-\ensuremath{\ensuremath{\ensuremath{\mathit{i}}}}\})$ .

3.2.1 Adding and Removing

If we have a reference to a node $\ensuremath{\ensuremath{\mathit{w}}}$ in a DLList and we want to insert a node $\ensuremath{\ensuremath{\mathit{u}}}$ before $\ensuremath{\ensuremath{\mathit{w}}}$ , then this is just a matter of setting $\ensuremath{\ensuremath{\ensuremath{\mathit{u}}.\ensuremath{\mathit{next}}}}=\ensuremath{\ensuremath{\ensuremath{\mathit{w}}}}$ , $\ensuremath{\ensuremath{\ensuremath{\mathit{u}}.\ensuremath{\mathit{prev}}}}=\ensuremath{\ensuremath{\ensuremath{\mathit{w}}.\ensuremath{\mathit{prev}}}}$ , and then adjusting $\ensuremath{\ensuremath{\mathit{u}}.\ensuremath{\mathit{prev}}.\ensuremath{\mathit{next}}}$ and $\ensuremath{\ensuremath{\mathit{u}}.\ensuremath{\mathit{next}}.\ensuremath{\mathit{prev}}}$ . (See Figure 3.3.) Thanks to the dummy node, there is no need to worry about $\ensuremath{\ensuremath{\mathit{w}}.\ensuremath{\mathit{prev}}}$ or $\ensuremath{\ensuremath{\mathit{w}}.\ensuremath{\mathit{next}}}$ not existing.

$\begin{leftbar} \begin{flushleft} \hspace*{1em} \ensuremath{\mathrm{add\_before}... ...bf{return}} \ensuremath{\ensuremath{\mathit{u}}}\\ \end{flushleft}\end{leftbar}$

**Figure 3.3:** Adding the node $\ensuremath{\ensuremath{\mathit{u}}}$ before the node $\ensuremath{\ensuremath{\mathit{w}}}$ in a DLList.
$\includegraphics[scale=0.90909]{figs-python/dllist-addbefore}$

Now, the list operation $\ensuremath{\mathrm{add}(\ensuremath{\mathit{i}},\ensuremath{\mathit{x}})}$ is trivial to implement. We find the $\ensuremath{\ensuremath{\mathit{i}}}$ th node in the DLList and insert a new node $\ensuremath{\ensuremath{\mathit{u}}}$ that contains $\ensuremath{\ensuremath{\mathit{x}}}$ just before it.

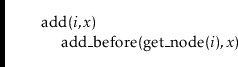
$\begin{leftbar} \begin{flushleft} \hspace*{1em} \ensuremath{\mathrm{add}(\ensure... ...\mathrm{get\_node}(\ensuremath{\mathit{i}}), x})\\ \end{flushleft}\end{leftbar}$

The only non-constant part of the running time of $\ensuremath{\mathrm{add}(\ensuremath{\mathit{i}},\ensuremath{\mathit{x}})}$ is the time it takes to find the $\ensuremath{\ensuremath{\mathit{i}}}$ th node (using $\ensuremath{\mathrm{get\_node}(\ensuremath{\mathit{i}})}$ ). Thus, $\ensuremath{\mathrm{add}(\ensuremath{\mathit{i}},\ensuremath{\mathit{x}})}$ runs in $O(1+\min\{\ensuremath{\ensuremath{\ensuremath{\mathit{i}}}}, \ensuremath{\ensu... ...{\ensuremath{\mathit{n}}}}-\ensuremath{\ensuremath{\ensuremath{\mathit{i}}}}\})$ time.

Removing a node $\ensuremath{\ensuremath{\mathit{w}}}$ from a DLList is easy. We only need to adjust pointers at $\ensuremath{\ensuremath{\mathit{w}}.\ensuremath{\mathit{next}}}$ and $\ensuremath{\ensuremath{\mathit{w}}.\ensuremath{\mathit{prev}}}$ so that they skip over $\ensuremath{\ensuremath{\mathit{w}}}$ . Again, the use of the dummy node eliminates the need to consider any special cases:

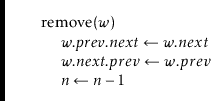
$\begin{leftbar} \begin{flushleft} \hspace*{1em} \ensuremath{\mathrm{remove}(\ens... ...math{\ensuremath{\mathit{n}} - 1}\hspace*{1em} }\\ \end{flushleft}\end{leftbar}$

Now the $\ensuremath{\mathrm{remove}(\ensuremath{\mathit{i}})}$ operation is trivial. We find the node with index $\ensuremath{\ensuremath{\mathit{i}}}$ and remove it:

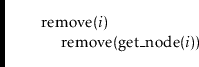
$\begin{leftbar} \begin{flushleft} \hspace*{1em} \ensuremath{\mathrm{remove}(\ens... ...e}(\mathrm{get\_node}(\ensuremath{\mathit{i}})})\\ \end{flushleft}\end{leftbar}$

Again, the only expensive part of this operation is finding the $\ensuremath{\ensuremath{\mathit{i}}}$ th node using $\ensuremath{\mathrm{get\_node}(\ensuremath{\mathit{i}})}$ , so $\ensuremath{\mathrm{remove}(\ensuremath{\mathit{i}})}$ runs in $O(1+\min\{\ensuremath{\ensuremath{\ensuremath{\mathit{i}}}}, \ensuremath{\ensu... ...{\ensuremath{\mathit{n}}}}-\ensuremath{\ensuremath{\ensuremath{\mathit{i}}}}\})$ time.

3.2.2 Summary

Theorem 3..2 A DLList implements the List interface. In this implementation, the $\ensuremath{\mathrm{get}(\ensuremath{\mathit{i}})}$ , $\ensuremath{\mathrm{set}(\ensuremath{\mathit{i}},\ensuremath{\mathit{x}})}$ , $\ensuremath{\mathrm{add}(\ensuremath{\mathit{i}},\ensuremath{\mathit{x}})}$ and $\ensuremath{\mathrm{remove}(\ensuremath{\mathit{i}})}$ operations run in $O(1+\min\{\ensuremath{\ensuremath{\ensuremath{\mathit{i}}}},\ensuremath{\ensur... ...{\ensuremath{\mathit{n}}}}-\ensuremath{\ensuremath{\ensuremath{\mathit{i}}}}\})$ time per operation.

It is worth noting that, if we ignore the cost of the $\ensuremath{\mathrm{get\_node}(\ensuremath{\mathit{i}})}$ operation, then all operations on a DLList take constant time. Thus, the only expensive part of operations on a DLList is finding the relevant node. Once we have the relevant node, adding, removing, or accessing the data at that node takes only constant time.

This is in sharp contrast to the array-based List implementations of Chapter 2; in those implementations, the relevant array item can be found in constant time. However, addition or removal requires shifting elements in the array and, in general, takes non-constant time.

For this reason, linked list structures are well-suited to applications where references to list nodes can be obtained through external means.