Next: 2.6 : A Space-Efficient Up: 2. Array-Based Lists Previous: 2.4 : Fast Deque Contents Index
Next, we present a data structure, the
![]() that
achieves the same performance bounds as an
that
achieves the same performance bounds as an
![]() by using
two
by using
two
![]() s. Although the asymptotic performance of the
s. Although the asymptotic performance of the
![]() is no better than that of the
is no better than that of the
![]() , it is
still worth studying, since it offers a good example of how to make a
sophisticated data structure by combining two simpler data structures.
, it is
still worth studying, since it offers a good example of how to make a
sophisticated data structure by combining two simpler data structures.
A
![]() represents a list using two
represents a list using two
![]() s. Recall that
an
s. Recall that
an
![]() is fast when the operations on it modify elements near
the end. A
is fast when the operations on it modify elements near
the end. A
![]() places two
places two
![]() s, called
s, called
![]() and
and
![]() , back-to-back so that operations are fast at either end.
, back-to-back so that operations are fast at either end.
ArrayStack<T> front; ArrayStack<T> back;
A
![]() does not explicitly store the number,
does not explicitly store the number,
![]() ,
of elements it contains. It doesn't need to, since it contains
,
of elements it contains. It doesn't need to, since it contains
![]() elements. Nevertheless, when
analyzing the
elements. Nevertheless, when
analyzing the
![]() we will still use
we will still use
![]() to denote the number
of elements it contains.
to denote the number
of elements it contains.
int size() {
return front.size() + back.size();
}
The
![]()
![]() stores the list elements that whose indices
are
stores the list elements that whose indices
are
![]() , but stores them in reverse order.
The
, but stores them in reverse order.
The
![]()
![]() contains list elements with indices
in
contains list elements with indices
in
![]() in the normal order. In this way,
in the normal order. In this way,
![]() and
and
![]() translate into appropriate calls to
translate into appropriate calls to
![]() or
or
![]() on either
on either
![]() or
or
![]() , which take
, which take ![]() time per operation.
time per operation.
T get(int i) {
if (i < front.size()) {
return front.get(front.size() - i - 1);
} else {
return back.get(i - front.size());
}
}
T set(int i, T x) {
if (i < front.size()) {
return front.set(front.size() - i - 1, x);
} else {
return back.set(i - front.size(), x);
}
}
Note that if an index
![]() , then it corresponds to the
element of
, then it corresponds to the
element of
![]() at position
at position
![]() , since the
elements of
, since the
elements of
![]() are stored in reverse order.
are stored in reverse order.
Adding and removing elements from a
![]() is illustrated in
Figure 2.4. The
is illustrated in
Figure 2.4. The
![]() operation manipulates either
operation manipulates either
![]() or
or
![]() , as appropriate:
, as appropriate:
![\includegraphics[scale=0.90909]{figs/dualarraydeque}](img981.png)
|
void add(int i, T x) {
if (i < front.size()) {
front.add(front.size() - i, x);
} else {
back.add(i - front.size(), x);
}
balance();
}
The
![]() method performs rebalancing of the two
method performs rebalancing of the two
![]() s
s
![]() and
and
![]() , by calling the
, by calling the
![]() method. The
implementation of
method. The
implementation of
![]() is described below, but for now it is
sufficient to know that
is described below, but for now it is
sufficient to know that
![]() ensures that, unless
ensures that, unless
![]() ,
,
![]() and
and
![]() do not differ by more than a factor
of 3. In particular,
do not differ by more than a factor
of 3. In particular,
![]() and
and
![]() .
.
Next we analyze the cost of
![]() , ignoring the cost of calls to
, ignoring the cost of calls to
![]() . If
. If
![]() , then
, then
![]() gets implemented
by the call to
gets implemented
by the call to
![]() . Since
. Since
![]() is an
is an
![]() , the cost of this is
, the cost of this is
Notice that the first case (2.1) occurs when
![]() .
The second case (2.2) occurs when
.
The second case (2.2) occurs when
![]() . When
. When
![]() , we cannot be sure whether the operation affects
, we cannot be sure whether the operation affects
![]() or
or
![]() , but in either case, the operation takes
, but in either case, the operation takes
![]() time, since
time, since
![]() and
and
![]() . Summarizing the situation, we have
. Summarizing the situation, we have
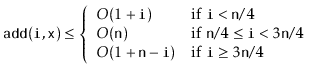
The
![]() operation and its analysis resemble the
operation and its analysis resemble the
![]() operation and analysis.
operation and analysis.
T remove(int i) {
T x;
if (i < front.size()) {
x = front.remove(front.size()-i-1);
} else {
x = back.remove(i-front.size());
}
balance();
return x;
}
Finally, we turn to the
![]() operation performed by
operation performed by
![]() and
and
![]() . This operation ensures that neither
. This operation ensures that neither
![]() nor
nor
![]() becomes too big (or too small). It ensures that, unless there are fewer
than two elements, each of
becomes too big (or too small). It ensures that, unless there are fewer
than two elements, each of
![]() and
and
![]() contain at least
contain at least
![]() elements. If this is not the case, then it moves elements between them
so that
elements. If this is not the case, then it moves elements between them
so that
![]() and
and
![]() contain exactly
contain exactly
![]() elements
and
elements
and
![]() elements, respectively.
elements, respectively.
void balance() {
if (3*front.size() < back.size()
|| 3*back.size() < front.size()) {
int n = front.size() + back.size();
int nf = n/2;
array<T> af(max(2*nf, 1));
for (int i = 0; i < nf; i++) {
af[nf-i-1] = get(i);
}
int nb = n - nf;
array<T> ab(max(2*nb, 1));
for (int i = 0; i < nb; i++) {
ab[i] = get(nf+i);
}
front.a = af;
front.n = nf;
back.a = ab;
back.n = nb;
}
}
Here there is little to analyze. If the
![]() operation does
rebalancing, then it moves
operation does
rebalancing, then it moves
![]() elements and this takes
elements and this takes
![]() time. This is bad, since
time. This is bad, since
![]() is called with each call to
is called with each call to
![]() and
and
![]() . However, the following lemma shows that, on
average,
. However, the following lemma shows that, on
average,
![]() only spends a constant amount of time per operation.
only spends a constant amount of time per operation.
We will perform our analysis using a technique knows as the
potential method.
Define the potential, ![]() , of the
, of the
![]() as the difference in size between
as the difference in size between
![]() and
and
![]() :
:
Observe that, immediately after a call to
![]() that shifts
elements, the potential,
that shifts
elements, the potential, ![]() , is at most 1, since
, is at most 1, since
Consider the situation immediately before a call to
![]() that
shifts elements and suppose, without loss of generality, that
that
shifts elements and suppose, without loss of generality, that
![]() is shifting elements because
is shifting elements because
![]() .
Notice that, in this case,
.
Notice that, in this case,
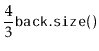 |
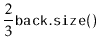 |
|||
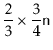 |
|||
The following theorem summarizes the properties of a
![]() :
:
opendatastructures.org