When studying the performance of a data structure, there are three things
that matter most:
- Correctness:
- The data structure should correctly implement
its interface.
- Time complexity:
- The running times of operations on the data
structure should be as small as possible.
- Space complexity:
- The data structure should use as little memory
as possible.
In this introductory text, we will take correctness as a given; we
won't consider data structures that give incorrect answers to queries or
don't perform updates properly. We will, however, see data structures
that make an extra effort to keep space usage to a minimum. This won't
usually affect the (asymptotic) running times of operations, but can
make the data structures a little slower in practice.
When studying running times in the context of data structures we tend to
come across three different kinds of running time guarantees:
- Worst-case running times:
- These are the strongest kind of running
time guarantees. If a data structure operation has a worst-case
running time of
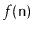 , then one of these operations never
takes longer than
, then one of these operations never
takes longer than
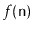 time.
time.
- Amortized running times:
- If we say that the amortized running
time of an operation in a data structure is
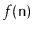 , then this means that
the cost of a typical operation is at most
, then this means that
the cost of a typical operation is at most
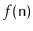 . More precisely,
if a data structure has an amortized running time of
. More precisely,
if a data structure has an amortized running time of
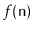 ,
then a sequence of
,
then a sequence of 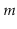 operations takes at most
operations takes at most
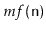 time.
Some individual operations may take more than
time.
Some individual operations may take more than
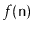 time but the
average, over the entire sequence of operations, is at most
time but the
average, over the entire sequence of operations, is at most
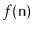 .
.
- Expected running times:
- If we say that the expected running time
of an operation on a data structure is
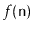 , this means that the
actual running time is a random variable (see Section 1.3.4)
and the expected value of this random variable is at most
, this means that the
actual running time is a random variable (see Section 1.3.4)
and the expected value of this random variable is at most
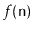 .
The randomization here is with respect to random choices made by the
data structure.
.
The randomization here is with respect to random choices made by the
data structure.
To understand the difference between worst-case, amortized, and expected
running times, it helps to consider a financial example. Consider the
cost of buying a house:
1.5.0.0.1 Worst-case versus amortized cost:
Suppose that a home costs $120000. In order to buy this home,
we might get a 120 month (10 year) mortgage with monthly payments of
$1200 per month. In this case, the worst-case monthly cost of paying
this mortgage is $1200 per month.
If we have enough cash on hand, we might choose to buy the house outright,
with one payment of $120000. In this case, over a period of 10 years,
the amortized monthly cost of buying this house is
This is much less than the $1200 per month we would have to pay if
we took out a mortgage.
1.5.0.0.2 Worst-case versus expected cost:
Next, consider the issue of fire insurance on our $120000 home.
By studying hundreds of thousands of cases, insurance companies have
determined that the expected amount of fire damage caused to a home
like ours is $10 per month. This is a very small number, since most
homes never have fires, a few homes may have some small fires that
cause a bit of smoke damage, and a tiny number of homes burn right to
their foundations. Based on this information, the insurance company
charges $15 per month for fire insurance.
Now it's decision time. Should we pay the $15 worst-case monthly cost
for fire insurance, or should we gamble and self-insure at an expected
cost of $10 per month? Clearly, the $10 per month costs less in
expectation, but we have to be able to accept the possibility that
the actual cost may be much higher. In the unlikely event that the
entire house burns down, the actual cost will be $120000.
These financial examples also offer insight into why we sometimes settle
for an amortized or expected running time over a worst-case running time.
It is often possible to get a lower expected or amortized running time
than a worst-case running time. At the very least, it is very often possible
to get a much simpler data structure if one is willing to settle for
amortized or expected running times.
opendatastructures.org