Next: 13.4 Discussion and Exercises Up: 13. Data Structures for Previous: 13.2 : Searching in Contents Index
: A Doubly-Logarithmic Time
The
is a vast--even exponential--improvement over the
in terms of query time, but the
and
operations are still not terribly fast. Furthermore, the space usage,
, is higher than the other
implementations
described in this book, which all use
space. These two
problems are related; if
operations build a structure of
size
, then the
operation requires at least on the
order of
time (and space) per operation.
The
, discussed next, simultaneously improves the space and
speed of
s. A
uses an
,
, but only
stores
values in
. In this way, the total space used by
is only
. Furthermore, only one out of every
or
operations in the
results in an
or
operation in
. By doing this, the average cost incurred
by calls to
's
and
operations is only constant.
The obvious question becomes: If
only stores
/
elements,
where do the remaining
elements go? These elements move
into secondary structures,
in this case an extended version of
treaps (Section 7.2). There are roughly
/
of these secondary
structures so, on average, each of them stores
items. Treaps
support logarithmic time
operations, so the operations on these
treaps will run in
time, as required.
More concretely, a
contains an
,
,
that contains a random sample of the data, where each element
appears in the sample independently with probability
.
For convenience, the value
, is always contained in
.
Let
denote the elements stored in
.
Associated with each element,
, is a treap,
, that stores
all values in the range
. This is illustrated
in Figure 13.7.
The
operation in a
is fairly easy. We search
for
in
and find some value
associated with the treap
. We then use the treap
method on
to answer
the query. The entire method is a one-liner:
![\includegraphics[scale=0.90909]{figs/yfast}](img5973.png)
T find(T x) {
return xft.find(YPair<T>(intValue(x))).t->find(x);
}
The first
operation (on
) takes
time.
The second
operation (on a treap) takes 
time, where
is the size of the treap. Later in this section, we will show that
the expected size of the treap is
so that this operation takes
time.13.1
Adding an element to a
is also fairly simple--most of
the time. The
method calls
to locate the treap,
, into which
should be inserted. It then calls
to
add
to
. At this point, it tosses a biased coin that comes up as
heads with probability
and as tails with probability
.
If this coin comes up heads, then
will be added to
.
This is where things get a little more complicated. When
is added to
, the treap
needs to be split into two treaps,
and
.
The treap
contains all the values less than or equal to
;
is the original treap,
, with the elements of
removed.
Once this is done, we add the pair
to
. Figure 13.8
shows an example.
bool add(T x) {
unsigned ix = intValue(x);
Treap1<T> *t = xft.find(YPair<T>(ix)).t;
if (t->add(x)) {
n++;
if (rand() % w == 0) {
Treap1<T> *t1 = (Treap1<T>*)t->split(x);
xft.add(YPair<T>(ix, t1));
}
return true;
}
return false;
return true;
}
![\includegraphics[scale=0.90909]{figs/yfast-add}](img6017.png)
|
to
takes
time. Exercise 7.12 shows
that splitting
into
and
can also be done in
expected time. Adding the pair (
,
) to
takes
time,
but only happens with probability
. Therefore, the expected
running time of the
operation is
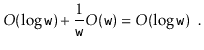
The
method undoes the work performed by
.
We use
to find the leaf,
, in
that contains the answer
to
. From
, we get the treap,
, containing
and remove
from
. If
was also stored in
(and
is not equal to
) then we remove
from
and add the
elements from
's treap to the treap,
, that is stored by
's
successor in the linked list. This is illustrated in
Figure 13.9.
bool remove(T x) {
unsigned ix = intValue(x);
XFastTrieNode1<YPair<T> > *u = xft.findNode(ix);
bool ret = u->x.t->remove(x);
if (ret) n--;
if (u->x.ix == ix && ix != UINT_MAX) {
Treap1<T> *t2 = u->child[1]->x.t;
t2->absorb(*u->x.t);
xft.remove(u->x);
}
return ret;
}
Finding the node
in
takes
expected time.
Removing
from
takes
expected time. Again,
Exercise 7.12 shows that merging all the elements of
into
can be done in
time. If necessary, removing
from
takes
time, but
is only contained in
with
probability
. Therefore, the expected time to remove an element
from a
is
.
Earlier in the discussion, we delayed arguing about the sizes of treaps in this structure until later. Before finishing this chapter, we prove the result we need.
be an integer stored in a
and let
denote the number of elements in the treap,
, that contains
.
Then
![$ \mathrm{E}[\ensuremath{\mathtt{n}}_\ensuremath{\mathtt{x}}] \le 2\ensuremath{\mathtt{w}}-1$](img6079.png){kind=small}
.
denote
the elements stored
in the
. The treap
contains some elements greater than
or equal to
. These are
,
where
is the only one of these elements in which the
biased coin toss performed in the
method turned up as heads.
In other words,
![$ \mathrm{E}[j]$](img6088.png){kind=small}
is equal to the expected number of biased coin
tosses required to obtain the first heads.13.2 Each coin toss is independent
and turns up as heads with probability
, so
![$ \mathrm{E}[j]\le\ensuremath{\mathtt{w}}$](img6093.png){kind=small}
.
(See Lemma 4.2 for an analysis of this for the case
.)
Similarly, the elements of
smaller than
are
where all these 
coin tosses turn up as
tails and the coin toss for
turns up as heads. Therefore,
![$ \mathrm{E}[k]\le\ensuremath{\mathtt{w}}-1$](img6100.png){kind=small}
, since this is the same coin tossing experiment considered
in the preceding paragraph, but one in which the last toss is not counted.
In summary,
, so
![$\displaystyle \mathrm{E}[\ensuremath{\mathtt{n}}_\ensuremath{\mathtt{x}}] = \ma...
...athrm{E}[j] + \mathrm{E}[k] \le 2\ensuremath{\mathtt{w}}-1 \enspace . \qedhere $](img6102.png){kind=small}
![\includegraphics[width=\textwidth ]{figs/yfast-sample}](img6103.png)
|
Lemma 13.1 was the last piece in the proof of the
following theorem, which summarizes the performance of the
:
implements the
interface for
-bit integers. A
supports the operations
,
, and
in
expected time per operation. The space used by a
that stores
values is
.
The
term in the space requirement comes from the fact that
always
stores the value
. The implementation could be modified (at the
expense of adding some extra cases to the code) so that it is unnecessary
to store this value. In this case, the space requirement in the theorem
becomes
.
![$ \mathrm{E}[r]=\ensuremath{\mathtt{w}}$](img5991.png){kind=small}
, then
![$ \mathrm{E}[\log r]
\le \log w$](img5992.png){kind=small}
.
never exceeds
. However, this only decreases
![$ \mathrm{E}[j]$](img6091.png){kind=small}
, so the upper bound still holds.
![\includegraphics[scale=0.90909]{figs/yfast-remove}](img6055.png)
