11.1 Comparison-Based Sorting

In this section, we present three sorting algorithms: merge-sort, quicksort, and heap-sort. Each of these algorithms takes an input array $\mathtt{a}$ and sorts the elements of $\mathtt{a}$ into non-decreasing order in $O(\ensuremath{\mathtt{n}}\log \ensuremath{\mathtt{n}})$ (expected) time. These algorithms are all comparison-based. These algorithms don't care what type of data is being sorted; the only operation they do on the data is comparisons using the $\mathtt{compare(a,b)}$ method. Recall, from Section 1.2.4, that $\mathtt{compare(a,b)}$ returns a negative value if $\ensuremath{\mathtt{a}}<\ensuremath{\mathtt{b}}$, a positive value if $\ensuremath{\mathtt{a}}>\ensuremath{\mathtt{b}}$, and zero if $\ensuremath{\mathtt{a}}=\ensuremath{\mathtt{b}}$.

11.1.1 Merge-Sort

The merge-sort algorithm is a classic example of recursive divide and conquer: If the length of $\mathtt{a}$ is at most 1, then $\mathtt{a}$ is already sorted, so we do nothing. Otherwise, we split $\mathtt{a}$ into two halves, $\ensuremath{\mathtt{a0}}=\ensuremath{\mathtt{a[0]}},\ldots,\ensuremath{\mathtt{a[n/2-1]}}$ and $\ensuremath{\mathtt{a1}}=\ensuremath{\mathtt{a[n/2]}},\ldots,\ensuremath{\mathtt{a[n-1]}}$. We recursively sort $\mathtt{a0}$ and $\mathtt{a1}$, and then we merge (the now sorted) $\mathtt{a0}$ and $\mathtt{a1}$ to get our fully sorted array $\mathtt{a}$:

void mergeSort(array<T> &a) {
  if (a.length <= 1) return;
  array<T> a0(0);
  array<T>::copyOfRange(a0, a, 0, a.length/2);
  array<T> a1(0);
  array<T>::copyOfRange(a1, a, a.length/2, a.length);
  mergeSort(a0);
  mergeSort(a1);
  merge(a0, a1, a);
}

An example is shown in Figure 11.1.

Figure 11.1: The execution of $\mathtt{mergeSort(a,c)}$

Compared to sorting, merging the two sorted arrays $\mathtt{a0}$ and $\mathtt{a1}$ is fairly easy. We add elements to $\mathtt{a}$ one at a time. If $\mathtt{a0}$ or $\mathtt{a1}$ is empty, then we add the next elements from the other (non-empty) array. Otherwise, we take the minimum of the next element in $\mathtt{a0}$ and the next element in $\mathtt{a1}$ and add it to $\mathtt{a}$:

void merge(array<T> &a0, array<T> &a1, array<T> &a) {
  int i0 = 0, i1 = 0;
  for (int i = 0; i < a.length; i++) {
    if (i0 == a0.length)
      a[i] = a1[i1++];
    else if (i1 == a1.length)
      a[i] = a0[i0++];
    else if (compare(a0[i0], a1[i1]) < 0)
      a[i] = a0[i0++];
    else
      a[i] = a1[i1++];
  }
}

Notice that the $\mathtt{merge(a0,a1,a,c)}$ algorithm performs at most $\ensuremath{\mathtt{n}}-1$ comparisons before running out of elements in one of $\mathtt{a0}$ or $\mathtt{a1}$.

To understand the running-time of merge-sort, it is easiest to think of it in terms of its recursion tree. Suppose for now that $\mathtt{n}$ is a power of two, so that $\ensuremath{\mathtt{n}}=2^{\log \ensuremath{\mathtt{n}}}$, and $\log \ensuremath{\mathtt{n}}$ is an integer. Refer to Figure 11.2. Merge-sort turns the problem of sorting $\mathtt{n}$ elements into two problems, each of sorting $\ensuremath{\mathtt{n}}/2$ elements. These two subproblem are then turned into two problems each, for a total of four subproblems, each of size $\ensuremath{\mathtt{n}}/4$. These four subproblems become eight subproblems, each of size $\ensuremath{\mathtt{n}}/8$, and so on. At the bottom of this process, $\ensuremath{\mathtt{n}}/2$ subproblems, each of size two, are converted into $\mathtt{n}$ problems, each of size one. For each subproblem of size $\ensuremath{\mathtt{n}}/2^{i}$, the time spent merging and copying data is $O(\ensuremath{\mathtt{n}}/2^i)$. Since there are $2^i$ subproblems of size $\ensuremath{\mathtt{n}}/2^i$, the total time spent working on problems of size $2^i$, not counting recursive calls, is

$$2^i\times O(\ensuremath{\mathtt{n}}/2^i) = O(\ensuremath{\mathtt{n}}) \enspace .$$

Therefore, the total amount of time taken by merge-sort is

$$\sum_{i=0}^{\log \ensuremath{\mathtt{n}}} O(\ensuremath{\mathtt{n}}) = O(\ensuremath{\mathtt{n}}\log \ensuremath{\mathtt{n}}) \enspace .$$

Figure 11.2: The merge-sort recursion tree.

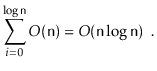
The proof of the following theorem is based on preceding analysis, but has to be a little more careful to deal with the cases where $\mathtt{n}$ is not a power of 2.

Theorem 11..1   The mergeSort(a) algorithm runs in $O(\ensuremath{\mathtt{n}}\log \ensuremath{\mathtt{n}})$ time and performs at most $\ensuremath{\mathtt{n}}\log \ensuremath{\mathtt{n}}$ comparisons.

Proof. The proof is by induction on $\ensuremath{\mathtt{n}}$. The base case, in which $\ensuremath{\mathtt{n}}=1$, is trivial; when presented with an array of length 0 or 1 the algorithm simply returns without performing any comparisons.

Merging two sorted lists of total length $\ensuremath{\mathtt{n}}$ requires at most $\ensuremath{\mathtt{n}}-1$ comparisons. Let $C(\ensuremath{\mathtt{n}})$ denote the maximum number of comparisons performed by $\mathtt{mergeSort(a,c)}$ on an array $\mathtt{a}$ of length $\mathtt{n}$. If $\ensuremath{\mathtt{n}}$ is even, then we apply the inductive hypothesis to the two subproblems and obtain

$$C(\ensuremath{\mathtt{n}}) \le \ensuremath{\mathtt{n}}-1 + 2C(\ensuremath{\mathtt{n}}/2)$$

$$\le \ensuremath{\mathtt{n}}-1 + 2((\ensuremath{\mathtt{n}}/2)\log(\ensuremath{\mathtt{n}}/2))$$

$$= \ensuremath{\mathtt{n}}-1 + \ensuremath{\mathtt{n}}\log(\ensuremath{\mathtt{n}}/2)$$

$$= \ensuremath{\mathtt{n}}-1 + \ensuremath{\mathtt{n}}\log \ensuremath{\mathtt{n}}-\ensuremath{\mathtt{n}}$$

$$< \ensuremath{\mathtt{n}}\log \ensuremath{\mathtt{n}} \enspace .$$

The case where $\ensuremath{\mathtt{n}}$ is odd is slightly more complicated. For this case, we use two inequalities that are easy to verify:

$$\log(x+1) \le \log(x) + 1 \enspace ,$$ (11.1)

for all $x\ge 1$ and

$$\log(x+1/2) + \log(x-1/2) \le 2\log(x) \enspace ,$$ (11.2)

for all $x\ge 1/2$. Inequality (11.1) comes from the fact that $\log(x)+1 = \log(2x)$ while (11.2) follows from the fact that $\log$ is a concave function. With these tools in hand we have, for odd $\mathtt{n}$,

$$C(\ensuremath{\mathtt{n}}) \le \ensuremath{\mathtt{n}}-1 + C(\lceil \ensuremath{\mathtt{n}}/2 \rceil) + C(\lfloor \ensuremath{\mathtt{n}}/2 \rfloor)$$

$$\le \ensuremath{\mathtt{n}}-1 + \lceil \ensuremath{\mathtt{n}}/2 ... ...\ensuremath{\mathtt{n}}/2 \rfloor\log \lfloor \ensuremath{\mathtt{n}}/2 \rfloor$$

$$= \ensuremath{\mathtt{n}}-1 + (\ensuremath{\mathtt{n}}/2 + 1/2)\l... ...2+1/2) + (\ensuremath{\mathtt{n}}/2 - 1/2) \log (\ensuremath{\mathtt{n}}/2-1/2)$$

$$\le \ensuremath{\mathtt{n}}-1 + \ensuremath{\mathtt{n}}\log(\ensu... ...2)(\log (\ensuremath{\mathtt{n}}/2+1/2) - \log (\ensuremath{\mathtt{n}}/2-1/2))$$

$$\le \ensuremath{\mathtt{n}}-1 + \ensuremath{\mathtt{n}}\log(\ensuremath{\mathtt{n}}/2) + 1/2$$

$$< \ensuremath{\mathtt{n}} + \ensuremath{\mathtt{n}}\log(\ensuremath{\mathtt{n}}/2)$$

$$= \ensuremath{\mathtt{n}} + \ensuremath{\mathtt{n}}(\log\ensuremath{\mathtt{n}}-1)$$

$$= \ensuremath{\mathtt{n}}\log\ensuremath{\mathtt{n}} \enspace . \qedhere$$

$\qedsymbol$

11.1.2 Quicksort

The quicksort algorithm is another classic divide and conquer algorithm. Unlike merge-sort, which does merging after solving the two subproblems, quicksort does all of its work upfront.

Quicksort is simple to describe: Pick a random pivot element, $\mathtt{x}$, from $\mathtt{a}$; partition $\mathtt{a}$ into the set of elements less than $\mathtt{x}$, the set of elements equal to $\mathtt{x}$, and the set of elements greater than $\mathtt{x}$; and, finally, recursively sort the first and third sets in this partition. An example is shown in Figure 11.3.

void quickSort(array<T> &a) {
  quickSort(a, 0, a.length);
}
void quickSort(array<T> &a, int i, int n) {
  if (n <= 1) return;
  T x = a[i + rand()%n];
  int p = i-1, j = i, q = i+n;
  // a[i..p]<x,  a[p+1..q-1]??x, a[q..i+n-1]>x
  while (j < q) {
    int comp = compare(a[j], x);
    if (comp < 0) {       // move to beginning of array
      a.swap(j++, ++p);
    } else if (comp > 0) {
      a.swap(j, --q);  // move to end of array
    } else {
      j++;              // keep in the middle
    }
  }
  // a[i..p]<x,  a[p+1..q-1]=x, a[q..i+n-1]>x
  quickSort(a, i, p-i+1);
  quickSort(a, q, n-(q-i));
}

Figure 11.3: An example execution of $\mathtt{quickSort(a,0,14)}$

All of this is done in place, so that instead of making copies of subarrays being sorted, the $\mathtt{quickSort(a,i,n,c)}$ method only sorts the subarray $\ensuremath{\mathtt{a[i]}},\ldots,\ensuremath{\mathtt{a[i+n-1]}}$. Initially, this method is invoked with the arguments $\mathtt{quickSort(a,0,a.length,c)}$.

At the heart of the quicksort algorithm is the in-place partitioning algorithm. This algorithm, without using any extra space, swaps elements in $\mathtt{a}$ and computes indices $\mathtt{p}$ and $\mathtt{q}$ so that

$$\ensuremath{\mathtt{a[i]}} \begin{cases} {}< \ensuremath{\mathtt... ...htt{q}}\le \ensuremath{\mathtt{i}} \le \ensuremath{\mathtt{n}}-1$} \end{cases}$$

This partitioning, which is done by the $\mathtt{while}$ loop in the code, works by iteratively increasing $\mathtt{p}$ and decreasing $\mathtt{q}$ while maintaining the first and last of these conditions. At each step, the element at position $\mathtt{j}$ is either moved to the front, left where it is, or moved to the back. In the first two cases, $\mathtt{j}$ is incremented, while in the last case, $\mathtt{j}$ is not incremented since the new element at position $\mathtt{j}$ has not yet been processed.

Quicksort is very closely related to the random binary search trees studied in Section 7.1. In fact, if the input to quicksort consists of $\mathtt{n}$ distinct elements, then the quicksort recursion tree is a random binary search tree. To see this, recall that when constructing a random binary search tree the first thing we do is pick a random element $\mathtt{x}$ and make it the root of the tree. After this, every element will eventually be compared to $\mathtt{x}$, with smaller elements going into the left subtree and larger elements into the right.

In quicksort, we select a random element $\mathtt{x}$ and immediately compare everything to $\mathtt{x}$, putting the smaller elements at the beginning of the array and larger elements at the end of the array. Quicksort then recursively sorts the beginning of the array and the end of the array, while the random binary search tree recursively inserts smaller elements in the left subtree of the root and larger elements in the right subtree of the root.

The above correspondence between random binary search trees and quicksort means that we can translate Lemma 7.1 to a statement about quicksort:

Lemma 11..1   When quicksort is called to sort an array containing the integers $0,\ldots,\ensuremath{\mathtt{n}}-1$, the expected number of times element $\mathtt{i}$ is compared to a pivot element is at most $H_{\ensuremath{\mathtt{i}}+1} + H_{\ensuremath{\mathtt{n}}-\ensuremath{\mathtt{i}}}$.

A little summing up of harmonic numbers gives us the following theorem about the running time of quicksort:

Theorem 11..2   When quicksort is called to sort an array containing $\mathtt{n}$ distinct elements, the expected number of comparisons performed is at most $2\ensuremath{\mathtt{n}}\ln \ensuremath{\mathtt{n}} + O(\ensuremath{\mathtt{n}})$.

Proof. Let $T$ be the number of comparisons performed by quicksort when sorting $\mathtt{n}$ distinct elements. Using Lemma 11.1 and linearity of expectation, we have:

$$\mathrm{E}[T] = \sum_{i=0}^{\ensuremath{\mathtt{n}}-1}(H_{\ensuremath{\mathtt{i}}+1}+H_{\ensuremath{\mathtt{n}}-\ensuremath{\mathtt{i}}})$$

$$= 2\sum_{i=1}^{\ensuremath{\mathtt{n}}}H_i$$

$$\le 2\sum_{i=1}^{\ensuremath{\mathtt{n}}}H_{\ensuremath{\mathtt{n}}}$$

$$\le 2\ensuremath{\mathtt{n}}\ln\ensuremath{\mathtt{n}} + 2\ensure... ...th{\mathtt{n}}\ln \ensuremath{\mathtt{n}} + O(\ensuremath{\mathtt{n}}) \qedhere$$

$\qedsymbol$

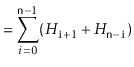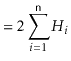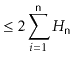Theorem 11.3 describes the case where the elements being sorted are all distinct. When the input array, $\mathtt{a}$, contains duplicate elements, the expected running time of quicksort is no worse, and can be even better; any time a duplicate element $\mathtt{x}$ is chosen as a pivot, all occurrences of $\mathtt{x}$ get grouped together and do not take part in either of the two subproblems.

Theorem 11..3   The $\mathtt{quickSort(a)}$ method runs in $O(\ensuremath{\mathtt{n}}\log \ensuremath{\mathtt{n}})$ expected time and the expected number of comparisons it performs is at most $2\ensuremath{\mathtt{n}}\ln \ensuremath{\mathtt{n}} +O(\ensuremath{\mathtt{n}})$.

11.1.3 Heap-sort

The heap-sort algorithm is another in-place sorting algorithm. Heap-sort uses the binary heaps discussed in Section 10.1. Recall that the $\mathtt{BinaryHeap}$ data structure represents a heap using a single array. The heap-sort algorithm converts the input array $\mathtt{a}$ into a heap and then repeatedly extracts the minimum value.

More specifically, a heap stores $\mathtt{n}$ elements in an array, $\mathtt{a}$, at array locations $\ensuremath{\mathtt{a[0]}},\ldots,\ensuremath{\mathtt{a[n-1]}}$ with the smallest value stored at the root, $\mathtt{a[0]}$. After transforming $\mathtt{a}$ into a $\mathtt{BinaryHeap}$, the heap-sort algorithm repeatedly swaps $\mathtt{a[0]}$ and $\mathtt{a[n-1]}$, decrements $\mathtt{n}$, and calls $\mathtt{trickleDown(0)}$ so that $\ensuremath{\mathtt{a[0]}},\ldots,\ensuremath{\mathtt{a[n-2]}}$ once again are a valid heap representation. When this process ends (because $\ensuremath{\mathtt{n}}=0$) the elements of $\mathtt{a}$ are stored in decreasing order, so $\mathtt{a}$ is reversed to obtain the final sorted order.^11.1Figure 11.4 shows an example of the execution of $\mathtt{heapSort(a,c)}$.

Figure 11.4: A snapshot of the execution of $\mathtt{heapSort(a,c)}$. The shaded part of the array is already sorted. The unshaded part is a $\mathtt{BinaryHeap}$. During the next iteration, element $5$ will be placed into array location $8$.

  void sort(array<T> &b) {
    BinaryHeap<T> h(b);
    while (h.n > 1) {
      h.a.swap(--h.n, 0);
      h.trickleDown(0);
    }
    b = h.a;
    b.reverse();
  }

A key subroutine in heap sort is the constructor for turning an unsorted array $\mathtt{a}$ into a heap. It would be easy to do this in $O(\ensuremath{\mathtt{n}}\log\ensuremath{\mathtt{n}})$ time by repeatedly calling the $\mathtt{BinaryHeap}$ $\mathtt{add(x)}$ method, but we can do better by using a bottom-up algorithm. Recall that, in a binary heap, the children of $\mathtt{a[i]}$ are stored at positions $\mathtt{a[2i+1]}$ and $\mathtt{a[2i+2]}$. This implies that the elements $\ensuremath{\mathtt{a}}[\lfloor\ensuremath{\mathtt{n}}/2\rfloor],\ldots,\ensuremath{\mathtt{a[n-1]}}$ have no children. In other words, each of $\ensuremath{\mathtt{a}}[\lfloor\ensuremath{\mathtt{n}}/2\rfloor],\ldots,\ensuremath{\mathtt{a[n-1]}}$ is a sub-heap of size 1. Now, working backwards, we can call $\mathtt{trickleDown(i)}$ for each $\ensuremath{\mathtt{i}}\in\{\lfloor \ensuremath{\mathtt{n}}/2\rfloor-1,\ldots,0\}$. This works, because by the time we call $\mathtt{trickleDown(i)}$, each of the two children of $\mathtt{a[i]}$ are the root of a sub-heap, so calling $\mathtt{trickleDown(i)}$ makes $\mathtt{a[i]}$ into the root of its own subheap.

  BinaryHeap(array<T> &b) : a(0) {
    a = b;
    n = a.length;
    for (int i = n/2-1; i >= 0; i--) {
      trickleDown(i);
    }
  }

The interesting thing about this bottom-up strategy is that it is more efficient than calling $\mathtt{add(x)}$ $\mathtt{n}$ times. To see this, notice that, for $\ensuremath{\mathtt{n}}/2$ elements, we do no work at all, for $\ensuremath{\mathtt{n}}/4$ elements, we call $\mathtt{trickleDown(i)}$ on a subheap rooted at $\mathtt{a[i]}$ and whose height is one, for $\ensuremath{\mathtt{n}}/8$ elements, we call $\mathtt{trickleDown(i)}$ on a subheap whose height is two, and so on. Since the work done by $\mathtt{trickleDown(i)}$ is proportional to the height of the sub-heap rooted at $\mathtt{a[i]}$, this means that the total work done is at most

$$\sum_{i=1}^{\log\ensuremath{\mathtt{n}}} O((i-1)\ensuremath{\math... ...i/2^{i} = O(2\ensuremath{\mathtt{n}}) = O(\ensuremath{\mathtt{n}}) \enspace .$$

The second-last equality follows by recognizing that the sum $\sum_{i=1}^{\infty} i/2^{i}$ is equal, by definition of expected value, to the expected number of times we toss a coin up to and including the first time the coin comes up as heads and applying Lemma 4.2.

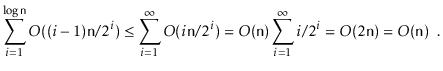
The following theorem describes the performance of $\mathtt{heapSort(a,c)}$.

Theorem 11..4   The $\mathtt{heapSort(a,c)}$ method runs in $O(\ensuremath{\mathtt{n}}\log \ensuremath{\mathtt{n}})$ time and performs at most $2\ensuremath{\mathtt{n}}\log \ensuremath{\mathtt{n}} + O(\ensuremath{\mathtt{n}})$ comparisons.

Proof. The algorithm runs in three steps: (1) transforming $\mathtt{a}$ into a heap, (2) repeatedly extracting the minimum element from $\mathtt{a}$, and (3) reversing the elements in $\mathtt{a}$. We have just argued that step 1 takes $O(\ensuremath{\mathtt{n}})$ time and performs $O(\ensuremath{\mathtt{n}})$ comparisons. Step 3 takes $O(\ensuremath{\mathtt{n}})$ time and performs no comparisons. Step 2 performs $\mathtt{n}$ calls to $\mathtt{trickleDown(0)}$. The $i$th such call operates on a heap of size $\ensuremath{\mathtt{n}}-i$ and performs at most $2\log(\ensuremath{\mathtt{n}}-i)$ comparisons. Summing this over $i$ gives

$$\sum_{i=0}^{\ensuremath{\mathtt{n}}-i} 2\log(\ensuremath{\mathtt{... ...ensuremath{\mathtt{n}} = 2\ensuremath{\mathtt{n}}\log \ensuremath{\mathtt{n}}$$

Adding the number of comparisons performed in each of the three steps completes the proof. $\qedsymbol$

11.1.4 A Lower-Bound for Comparison-Based Sorting

We have now seen three comparison-based sorting algorithms that each run in $O(\ensuremath{\mathtt{n}}\log \ensuremath{\mathtt{n}})$ time. By now, we should be wondering if faster algorithms exist. The short answer to this question is no. If the only operations allowed on the elements of $\mathtt{a}$ are comparisons, then no algorithm can avoid doing roughly $\ensuremath{\mathtt{n}}\log \ensuremath{\mathtt{n}}$ comparisons. This is not difficult to prove, but requires a little imagination. Ultimately, it follows from the fact that

$$\log(\ensuremath{\mathtt{n}}!) = \log \ensuremath{\mathtt{n}} +... ...athtt{n}}\log \ensuremath{\mathtt{n}} - O(\ensuremath{\mathtt{n}}) \enspace .$$

(Proving this fact is left as Exercise 11.10.)

We will start by focusing our attention on deterministic algorithms like merge-sort and heap-sort and on a particular fixed value of $\mathtt{n}$. Imagine such an algorithm is being used to sort $\mathtt{n}$ distinct elements. The key to proving the lower-bound is to observe that, for a deterministic algorithm with a fixed value of $\mathtt{n}$, the first pair of elements that are compared is always the same. For example, in $\mathtt{heapSort(a,c)}$, when $\mathtt{n}$ is even, the first call to $\mathtt{trickleDown(i)}$ is with $\mathtt{i=n/2-1}$ and the first comparison is between elements $\mathtt{a[n/2-1]}$ and $\mathtt{a[n-1]}$.

Since all input elements are distinct, this first comparison has only two possible outcomes. The second comparison done by the algorithm may depend on the outcome of the first comparison. The third comparison may depend on the results of the first two, and so on. In this way, any deterministic comparison-based sorting algorithm can be viewed as a rooted binary comparison tree. Each internal node, $\mathtt{u}$, of this tree is labelled with a pair of indices $\mathtt{u.i}$ and $\mathtt{u.j}$. If $\ensuremath{\mathtt{a[u.i]}}<\ensuremath{\mathtt{a[u.j]}}$ the algorithm proceeds to the left subtree, otherwise it proceeds to the right subtree. Each leaf $\mathtt{w}$ of this tree is labelled with a permutation $\ensuremath{\mathtt{w.p[0]}},\ldots,\ensuremath{\mathtt{w.p[n-1]}}$ of $0,\ldots,\ensuremath{\mathtt{n}}-1$. This permutation represents the one that is required to sort $\mathtt{a}$ if the comparison tree reaches this leaf. That is,

$$\ensuremath{\mathtt{a[w.p[0]]}}<\ensuremath{\mathtt{a[w.p[1]]}}<\cdots<\ensuremath{\mathtt{a[w.p[n-1]]}} \enspace .$$

An example of a comparison tree for an array of size $\mathtt{n=3}$ is shown in Figure 11.5.

Figure 11.5: A comparison tree for sorting an array $\ensuremath{\mathtt{a[0]}},\ensuremath{\mathtt{a[1]}},\ensuremath{\mathtt{a[2]}}$ of length $\mathtt{n=3}$.

The comparison tree for a sorting algorithm tells us everything about the algorithm. It tells us exactly the sequence of comparisons that will be performed for any input array, $\mathtt{a}$, having $\mathtt{n}$ distinct elements and it tells us how the algorithm will reorder $\mathtt{a}$ in order to sort it. Consequently, the comparison tree must have at least $\ensuremath{\mathtt{n}}!$ leaves; if not, then there are two distinct permutations that lead to the same leaf; therefore, the algorithm does not correctly sort at least one of these permutations.

For example, the comparison tree in Figure 11.6 has only $4< 3!=6$ leaves. Inspecting this tree, we see that the two input arrays $3,1,2$ and $3,2,1$ both lead to the rightmost leaf. On the input $3,1,2$ this leaf correctly outputs $\ensuremath{\mathtt{a[1]}}=1,\ensuremath{\mathtt{a[2]}}=2,\ensuremath{\mathtt{a[0]}}=3$. However, on the input $3,2,1$, this node incorrectly outputs $\ensuremath{\mathtt{a[1]}}=2,\ensuremath{\mathtt{a[2]}}=1,\ensuremath{\mathtt{a[0]}}=3$. This discussion leads to the primary lower-bound for comparison-based algorithms.

Figure 11.6: A comparison tree that does not correctly sort every input permutation.

Theorem 11..5   For any deterministic comparison-based sorting algorithm $\mathcal{A}$ and any integer $\ensuremath{\mathtt{n}}\ge 1$, there exists an input array $\mathtt{a}$ of length $\mathtt{n}$ such that $\mathcal{A}$ performs at least $\log(\ensuremath{\mathtt{n}}!) = \ensuremath{\mathtt{n}}\log\ensuremath{\mathtt{n}}-O(\ensuremath{\mathtt{n}})$ comparisons when sorting $\mathtt{a}$.

Proof. By the preceding discussion, the comparison tree defined by $\mathcal{A}$ must have at least $\ensuremath{\mathtt{n}}!$ leaves. An easy inductive proof shows that any binary tree with $k$ leaves has a height of at least $\log k$. Therefore, the comparison tree for $\mathcal{A}$ has a leaf, $\mathtt{w}$, with a depth of at least $\log(\ensuremath{\mathtt{n}}!)$ and there is an input array $\mathtt{a}$ that leads to this leaf. The input array $\mathtt{a}$ is an input for which $\mathcal{A}$ does at least $\log(\ensuremath{\mathtt{n}}!)$ comparisons. $\qedsymbol$

Theorem 11.5 deals with deterministic algorithms like merge-sort and heap-sort, but doesn't tell us anything about randomized algorithms like quicksort. Could a randomized algorithm beat the $\log(\ensuremath{\mathtt{n}}!)$ lower bound on the number of comparisons? The answer, again, is no. Again, the way to prove it is to think differently about what a randomized algorithm is.

In the following discussion, we will assume that our decision trees have been ``cleaned up'' in the following way: Any node that can not be reached by some input array $\mathtt{a}$ is removed. This cleaning up implies that the tree has exactly $\ensuremath{\mathtt{n}}!$ leaves. It has at least $\ensuremath{\mathtt{n}}!$ leaves because, otherwise, it could not sort correctly. It has at most $\ensuremath{\mathtt{n}}!$ leaves since each of the possible $\ensuremath{\mathtt{n}}!$ permutation of $\mathtt{n}$ distinct elements follows exactly one root to leaf path in the decision tree.

We can think of a randomized sorting algorithm, $\mathcal{R}$, as a deterministic algorithm that takes two inputs: The input array $\mathtt{a}$ that should be sorted and a long sequence $b=b_1,b_2,b_3,\ldots,b_m$ of random real numbers in the range $[0,1]$. The random numbers provide the randomization for the algorithm. When the algorithm wants to toss a coin or make a random choice, it does so by using some element from $b$. For example, to compute the index of the first pivot in quicksort, the algorithm could use the formula $\lfloor n b_1\rfloor$.

Now, notice that if we fix $b$ to some particular sequence $\hat{b}$ then $\mathcal{R}$ becomes a deterministic sorting algorithm, $\mathcal{R}(\hat{b})$, that has an associated comparison tree, $\mathcal{T}(\hat{b})$. Next, notice that if we select $\mathtt{a}$ to be a random permutation of $\{1,\ldots,\ensuremath{\mathtt{n}}\}$, then this is equivalent to selecting a random leaf, $\mathtt{w}$, from the $\ensuremath{\mathtt{n}}!$ leaves of $\mathcal{T}(\hat{b})$.

Exercise 11.12 asks you to prove that, if we select a random leaf from any binary tree with $k$ leaves, then the expected depth of that leaf is at least $\log k$. Therefore, the expected number of comparisons performed by the (deterministic) algorithm $\mathcal{R}(\hat{b})$ when given an input array containing a random permutation of $\{1,\ldots,n\}$ is at least $\log(\ensuremath{\mathtt{n}}!)$. Finally, notice that this is true for every choice of $\hat{b}$, therefore it holds even for $\mathcal{R}$. This completes the proof of the lower-bound for randomized algorithms.

Theorem 11..6   For any integer $n\ge 1$ and any (deterministic or randomized) comparison-based sorting algorithm $\mathcal{A}$, the expected number of comparisons done by $\mathcal{A}$ when sorting a random permutation of $\{1,\ldots,n\}$ is at least $\log(\ensuremath{\mathtt{n}}!) = \ensuremath{\mathtt{n}}\log\ensuremath{\mathtt{n}}-O(\ensuremath{\mathtt{n}})$.

Footnotes

... order.^11.1

The algorithm could alternatively redefine the $\mathtt{compare(x,y)}$ function so that the heap sort algorithm stores the elements directly in ascending order.