7.1 Random Binary Search Trees

Consider the two binary search trees shown in Figure 7.1. The one on the left is a list and the other is a perfectly balanced binary search tree. The one on the left has height $\ensuremath{\mathtt{n}}-1=14$ and the one on the right has height three.

Figure 7.1: Two binary search trees containing the integers $0,\ldots ,14$.

Imagine how these two trees could have been constructed. The one on the left occurs if we start with an empty BinarySearchTree and add the sequence

$$\langle 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14 \rangle \enspace .$$

No other sequence of additions will create this tree (as you can prove by induction on $\mathtt{n}$). On the other hand, the tree on the right can be created by the sequence

$$\langle 7,3,11,1,5,9,13,0,2,4,6,8,10,12,14 \rangle \enspace .$$

Other sequences work as well, including

$$\langle 7,3,1,5,0,2,4,6,11,9,13,8,10,12,14 \rangle \enspace ,$$

and

$$\langle 7,3,1,11,5,0,2,4,6,9,13,8,10,12,14 \rangle \enspace .$$

In fact, there are $21,964,800$ addition sequences that generate the tree on the right and only one that generates the tree on the left.

The above example gives some anecdotal evidence that, if we choose a random permutation of $0,\ldots ,14$, and add it into a binary search tree then we are more likely to get a very balanced tree (the right side of Figure 7.1) than we are to get a very unbalanced tree (the left side of Figure 7.1).

We can formalize this notion by studying random binary search trees. A random binary search tree of size $\mathtt{n}$ is obtained in the following way: Take a random permutation $\ensuremath{\mathtt{x}}_0,\ldots,\ensuremath{\mathtt{x}}_{\ensuremath{\mathtt{n}}-1}$ of $0,\ldots,\ensuremath{\mathtt{n}}-1$ and add its elements, one by one, into a BinarySearchTree.

Note that the values $0,\ldots,\ensuremath{\mathtt{n}}-1$ could be replaced by any ordered set of $\mathtt{n}$ elements without changing any of the properties of the random binary search tree. The element $\ensuremath{\mathtt{x}}\in\{0,\ldots,\ensuremath{\mathtt{n}}-1\}$ is simply standing in for the element of rank $\mathtt{x}$ in an ordered set of size $\mathtt{n}$.

Before we can present our main result about random binary search trees, we must take some time for a short digression to discuss a type of number that comes up frequently when studying randomized structures. For a non-negative integer, $k$, the $k$-th harmonic number, denoted $H_k$, is defined as

$$H_k = 1 + 1/2 + 1/3 + \cdots + 1/k \enspace .$$

The harmonic number $H_k$ has no simple closed form, but it is very closely related to the natural logarithm of $k$. In particular,

$$\ln k \le H_k \le \ln k + 1 \enspace .$$

Readers who have studied calculus might notice that this is because the integral $\int_1^k\! (1/x)\, \mathrm{d}x= \ln k$. Keeping in mind that an integral can be interpreted as the area between a curve and the $x$-axis, the value of $H_k$ can be lower-bounded by the integral $\int_1^k\! (1/x)\, \mathrm{d}x$ and upper-bounded by $1+ \int_1^k\! (1/x)\, \mathrm{d}x$. (See Figure 7.2 for a graphical explanation.)

Figure 7.2: The $k$th harmonic number $H_k=\sum_{i=1}^k 1/i$ is upper-bounded by $1+ \int_1^k\! (1/x)\, \mathrm{d}x$ and lower-bounded by $\int_1^k\! (1/x)\, \mathrm{d}x$.

Lemma 7..1   In a random binary search tree of size $\mathtt{n}$, the following statements hold:

1. For any $\ensuremath{\mathtt{x}}\in\{0,\ldots,\ensuremath{\mathtt{n}}-1\}$, the expected length of the search path for $\mathtt{x}$ is $H_{\ensuremath{\mathtt{x}}+1} + H_{\ensuremath{\mathtt{n}}-\ensuremath{\mathtt{x}}} - O(1)$.¹
2. For any $\ensuremath{\mathtt{x}}\in(-1,n)\setminus\{0,\ldots,\ensuremath{\mathtt{n}}-1\}$, the expected length of the search path for $\mathtt{x}$ is $H_{\lceil\ensuremath{\mathtt{x}}\rceil} + H_{\ensuremath{\mathtt{n}}-\lceil\ensuremath{\mathtt{x}}\rceil}$.

We will prove Lemma 7.1 in the next section. For now, consider what the two parts of Lemma 7.1 tell us. The first part tells us that if we search for an element in a tree of size $\mathtt{n}$, then the expected length of the search path is at most $2\ln n + O(1)$. The second part tells us the same thing about searching for a value not stored in the tree. When we compare the two parts of the lemma, we see that it is only slightly faster to search for something that is in a tree compared to something that is not in a tree.

7.1.1 Proof of Lemma 7.1

The key observation needed to prove Lemma 7.1 is the following: The search path for a value $\mathtt{x}$ in the open interval $(-1,\ensuremath{\mathtt{n}})$ in a random binary search tree, $T$, contains the node with key $i < \ensuremath{\mathtt{x}}$ if and only if, in the random permutation used to create $T$, $i$ appears before any of $\{i+1,i+2,\ldots,\lfloor\ensuremath{\mathtt{x}}\rfloor\}$.

To see this, refer to Figure 7.3 and notice that, until some value in $\{i,i+1,\ldots,\lfloor\ensuremath{\mathtt{x}}\rfloor\}$ is added, the search paths for each value in the open interval $(i-1,\lfloor\ensuremath{\mathtt{x}}\rfloor+1)$ are identical. (Remember that for two search values to have different search paths, there must be some element in the tree that compares differently with them.) Let $j$ be the first element in $\{i,i+1,\ldots,\lfloor\ensuremath{\mathtt{x}}\rfloor\}$ to appear in the random permutation. Notice that $j$ is now and will always be on the search path for $\mathtt{x}$. If $j\neq i$ then the node $\ensuremath{\mathtt{u}}_j$ containing $j$ is created before the node $\ensuremath{\mathtt{u}}_i$ that contains $i$. Later, when $i$ is added, it will be added to the subtree rooted at $\ensuremath{\mathtt{u}}_j\ensuremath{\mathtt{.left}}$, since $i<j$. On the other hand, the search path for $\mathtt{x}$ will never visit this subtree because it will proceed to $\ensuremath{\mathtt{u}}_j\ensuremath{\mathtt{.right}}$ after visiting $\ensuremath{\mathtt{u}}_j$.

Figure 7.3: The value $i < \ensuremath{\mathtt{x}}$ is on the search path for $\mathtt{x}$ if and only if $i$ is the first element among $\{i,i+1,\ldots,\lfloor\ensuremath{\mathtt{x}}\rfloor\}$ added to the tree.

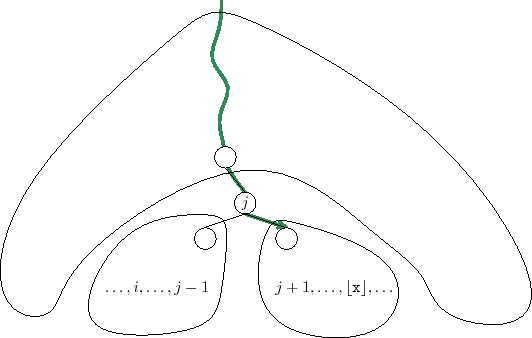
Similarly, for $i>\ensuremath{\mathtt{x}}$, $i$ appears in the search path for $\mathtt{x}$ if and only if $i$ appears before any of $\{\lceil\ensuremath{\mathtt{x}}\rceil, \lceil\ensuremath{\mathtt{x}}\rceil+1,\ldots,i-1\}$ in the random permutation used to create $T$.

Notice that, if we start with a random permutation of $\{0,\ldots,\ensuremath{\mathtt{n}}\}$, then the subsequences containing only $\{i,i+1,\ldots,\lfloor\ensuremath{\mathtt{x}}\rfloor\}$ and $\{\lceil\ensuremath{\mathtt{x}}\rceil, \lceil\ensuremath{\mathtt{x}}\rceil+1,\ldots,i-1\}$ are also random permutations of their respective elements. Each element, then, in the subsets $\{i,i+1,\ldots,\lfloor\ensuremath{\mathtt{x}}\rfloor\}$ and $\{\lceil\ensuremath{\mathtt{x}}\rceil, \lceil\ensuremath{\mathtt{x}}\rceil+1,\ldots,i-1\}$ is equally likely to appear before any other in its subset in the random permutation used to create $T$. So we have

$$\Pr\{$$$$\mbox{$i$\ is on the search path for \ensuremath{\mathtt{x}}}$$$$\} = \left\{ \begin{array}{ll} 1/(\lfloor\ensuremath{\mathtt{x}... ...+1) & \mbox{if $i > \ensuremath{\mathtt{x}}$} \end{array}\right . \enspace .$$

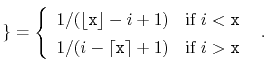
With this observation, the proof of Lemma 7.1 involves some simple calculations with harmonic numbers:

Proof. [Proof of Lemma 7.1] Let $I_i$ be the indicator random variable that is equal to one when $i$ appears on the search path for $\mathtt{x}$ and zero otherwise. Then the length of the search path is given by

$$\sum_{i\in\{0,\ldots,\ensuremath{\mathtt{n}}-1\}\setminus\{\ensuremath{\mathtt{x}}\}} I_i$$

so, if $\ensuremath{\mathtt{x}}\in\{0,\ldots,\ensuremath{\mathtt{n}}-1\}$, the expected length of the search path is given by (see Figure 7.4.a)

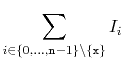
$$\mathrm{E}\left[\sum_{i=0}^{\ensuremath{\mathtt{x}}-1} I_i + \sum_{i=\ensuremath{\mathtt{x}}+1}^{\ensuremath{\mathtt{n}}-1} I_i\right] = \sum_{i=0}^{\ensuremath{\mathtt{x}}-1} \mathrm{E}\left[I_i\righ... ...nsuremath{\mathtt{x}}+1}^{\ensuremath{\mathtt{n}}-1} \mathrm{E}\left[I_i\right]$$

$$= \sum_{i=0}^{\ensuremath{\mathtt{x}}-1} 1/(\lfloor\ensuremath{\m... ...{x}}+1}^{\ensuremath{\mathtt{n}}-1} 1/(i-\lceil\ensuremath{\mathtt{x}}\rceil+1)$$

$$= \sum_{i=0}^{\ensuremath{\mathtt{x}}-1} 1/(\ensuremath{\mathtt{x... ...math{\mathtt{x}}+1}^{\ensuremath{\mathtt{n}}-1} 1/(i-\ensuremath{\mathtt{x}}+1)$$

$$= \frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{\ensuremath{\mathtt{x}}+1}$$

$${} + \frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{\ensuremath{\mathtt{n}}-\ensuremath{\mathtt{x}}}$$

$$= H_{\ensuremath{\mathtt{x}}+1} + H_{\ensuremath{\mathtt{n}}-\ensuremath{\mathtt{x}}} - 2 \enspace .$$

The corresponding calculations for a search value $\ensuremath{\mathtt{x}}\in(-1,n)\setminus\{0,\ldots,\ensuremath{\mathtt{n}}-1\}$ are almost identical (see Figure 7.4.b). $\qedsymbol$

Figure 7.4: The probabilities of an element being on the search path for $\mathtt{x}$ when (a)  $\mathtt{x}$ is an integer and (b) when $\mathtt{x}$ is not an integer.

(a)

(b)

7.1.2 Summary

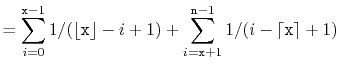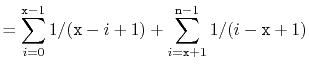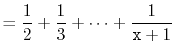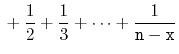The following theorem summarizes the performance of a random binary search tree:

Theorem 7..1   A random binary search tree can be constructed in $O(\ensuremath{\mathtt{n}}\log \ensuremath{\mathtt{n}})$ time. In a random binary search tree, the $\mathtt{find(x)}$ operation takes $O(\log \ensuremath{\mathtt{n}})$ expected time.

Footnotes

....¹

The expressions $\ensuremath{\mathtt{x}}+1$ and $\ensuremath{\mathtt{n}}-\ensuremath{\mathtt{x}}$ can be interpreted respectively as the number of elements in the tree less than or equal to $\mathtt{x}$ and the number of elements in the tree greater than or equal to $\mathtt{x}$.