Next: 2.7 Discussion and Exercises Up: 2. Array-Based Lists Previous: 2.5 : Building a Contents
: A Space-Efficient Array Stack
One of the drawbacks of all previous data structures in this chapter
is that, because they store their data in one or two arrays, and they
avoid resizing these arrays too often, the arrays are frequently not
very full. For example, immediately after a
operation on
an
, the backing array
is only half full. Even worse,
there are times when only 
of
contains data.
In this section, we discuss a data structure, the
,
that addresses the problem of wasted space. The
stores
elements using
arrays. In these arrays, at
most
array locations are unused at any time. All
remaining array locations are used to store data. Therefore, these
data structures waste at most
space when storing
elements.
A
stores its elements in a list of
arrays called blocks that are numbered
.
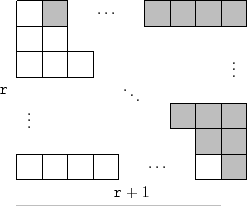
See Figure 2.5. Block 
contains 
elements.
Therefore, all
blocks contain a total of
ArrayStack<T*> blocks; int n;
|
The elements of the list are laid out in the blocks as we might
expect. The list element with index 0 is stored in block 0, the
elements with list indices 1 and 2 are stored in block 1, the elements
with list indices 3, 4, and 5 are stored in block 2, and so on. The
main problem we have to address is that of determining, given an index
, which block contains
as well as the index corresponding to
within that block.
Determining the index of
within its block turns out to be easy. If
index
is in block
, then the number of elements in blocks
is
. Therefore,
is stored at location
. Somewhat more challenging is the problem of determining
the value of
. The number of elements that have indices less than
or equal to
is
. On the other hand, the number of elements
in blocks 0,...,b is
. Therefore,
is the smallest
integer such that
has two
solutions:
and
.
The second solution makes no sense in our application since it always
gives a negative value. Therefore, we obtain the solution
. In general, this solution is not an integer, but
going back to our inequality, we want the smallest integer
such that
. This is simply
int i2b(int i) {
double db = (-3.0 + sqrt(9 + 8*i)) / 2.0;
int b = (int)ceil(db);
return b;
}
With this out of the way, the
and
methods are straightforward. We first compute the appropriate block
and the appropriate index
within the block and then perform the appropriate operation:
T get(int i) {
int b = i2b(i);
int j = i - b*(b+1)/2;
return blocks.get(b)[j];
}
T set(int i, T x) {
int b = i2b(i);
int j = i - b*(b+1)/2;
T y = blocks.get(b)[j];
blocks.get(b)[j] = x;
return y;
}
If we use any of the data structures in this chapter for representing the
list, then
and
will each run in constant time.
The
method will, by now, look familiar. We first check if
our data structure is full, by checking if the number of blocks
is such that
and, if so, we call
to add another block. With this done, we shift elements with indices
to the right by one position to make room for the
new element with index
:
void add(int i, T x) {
int r = blocks.size();
if (r*(r+1)/2 < n + 1) grow();
n++;
for (int j = n-1; j > i; j--)
set(j, get(j-1));
set(i, x);
}
The
method does what we expect. It adds a new block:
void grow() {
blocks.add(blocks.size(), new T[blocks.size()+1]);
}
Ignoring the cost of the
operation, the cost of an
operation is dominated by the cost of shifting and is therefore
, just like an
.
The
operation is similar to
. It shifts the
elements with indices
left by one position and then,
if there is more than one empty block, it calls the
method
to remove all but one of the unused blocks:
T remove(int i) {
T x = get(i);
for (int j = i; j < n-1; j++)
set(j, get(j+1));
n--;
int r = blocks.size();
if ((r-2)*(r-1)/2 >= n) shrink();
return x;
}
void shrink() {
int r = blocks.size();
while (r > 0 && (r-2)*(r-1)/2 >= n) {
delete [] blocks.remove(blocks.size()-1);
r--;
}
}
Once again, ignoring the cost of the
operation, the cost of
a
operation is dominated by the cost of shifting and is
therefore
.
The above analysis of
and
does not account for
the cost of
and
. Note that, unlike the
operation,
and
do not do any
copying of data. They only allocate or free an array of size
. In
some environments, this takes only constant time, while in others, it
may require
time.
We note that, immediately after a call to
or
, the
situation is clear. The final block is completely empty and all other
blocks are completely full. Another call to
or
will
not happen until at least
elements have been added or removed.
Therefore, even if
and
take
time, this
cost can be amortized over at least
or
operations, so that the amortized cost of
and
is
per operation.
Next, we analyze the amount of extra space used by a
.
In particular, we want to count any space used by a
that is not an array element currently used to hold a list element. We call all such space wasted space.
The
operation ensures that a
never has
more than 2 blocks that are not completely full. The number of blocks,
, used by a
that stores
elements therefore
satisfies
and
, so the space wasted by these
two blocks is at most
. If we store the blocks
in (for example) an
, then the amount of space wasted by the
that stores those
blocks is also
. The
other space needed for storing
and other accounting information is .
Therefore, the total amount of wasted space in a
is
.
Next, we argue that this space usage is optimal for any data structure
that starts out empty and can support the addition of one item at a
time. More precisely, we will show that, at some point during the
addition of
items, the data structure is wasting an amount of
space at least in
(though it may be only wasted for a
moment).
Suppose we start with an empty data structure and we add
items
one at a time. At the end of this process, all
items are stored
in the structure and they are distributed among a collection of
memory blocks. If
, then the data structure must be
using
pointers (or references) to keep track of these
blocks,
and this is wasted space. On the other hand, if
then, by the pigeonhole principle, some block must have size at least
. Consider the moment at which this block was
first allocated. Immediately after it was allocated, this block was
empty, and was therefore wasting
space. Therefore, at some
point in time during the insertion of
elements, the data structure was
wasting
space.
The following theorem summarizes the performance of the
data structure:
implements the
interface. Ignoring the cost of
calls to
and
, a
supports the operations
and
in time per operation; and
and
in
time per operation.
, any sequence of 
and
operations results in a total of 
time spent during all calls to
and
.
The space (measured in words)3 used by a
that stores
elements is
.
A reader who has had some exposure to models of computation may notice
that the
, as described above, does not fit into
the usual word-RAM model of computation () because it
requires taking square roots. The square root operation is generally
not considered a basic operation and is therefore not usually part of
the word-RAM model.
In this section, we take time to show that the square root operation can
be implemented efficiently. In particular, we show that for any integer
,
can be computed
in constant-time, after
preprocessing that creates two
arrays of length
.
The following lemma shows that we can reduce the problem of computing the square root of
to the square root of a related value
.
.
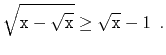
Start by restricting the problem a little, and assume that
, so that
, i.e.,
is an
integer having
bits in its binary representation. We can take
. Now,
satisfies
the conditions of Lemma 2.3, so
.
Furthermore,
has all of its lower-order
bits
equal to 0, so there are only
. This means that we can use an array,
,
that stores the value of
for each possible
value of
. A little more precisely, we have
![$\displaystyle \ensuremath{\mathtt{sqrttab}}[i]
= \left\lfloor
\sqrt{i 2^{\lfloor \ensuremath{\mathtt{r}}/2\rfloor}}
\right\rfloor \enspace .
$](img450.png){kind=small}
![$ \ensuremath{\mathtt{sqrttab}}[i]$](img451.png){kind=small}
is within 2 of
for all
.
Stated another way, the array entry
![$ \ensuremath{\mathtt{s}}=\ensuremath{\mathtt{sqrttab}}[\ensuremath{\mathtt{x}}\ensuremath{\mathtt{>>}}\lfloor \ensuremath{\mathtt{r}}/2\rfloor]$](img454.png){kind=small}
is either equal to
,
, or
. From
we can determine the value
of
by
incrementing
until
.
int sqrt(int x, int r) {
int s = sqrtab[x>>r/2];
while ((s+1)*(s+1) <= x) s++; // executes at most twice
return s;
}
Now, this only works for
and
is a special table that only works for a particular value
of
. To overcome this, we could compute
different
arrays, one for each possible
value of
. The sizes of these tables form an exponential sequence whose largest value is at most
, so the total size of all tables is
.
However, it turns out that more than one
array is unnecessary;
we only need one
array for the value
. Any value
with
can be upgraded
by multiplying
by
and using the equation
is in the range
so we can look up its square root
in
. The following code implements this idea to compute
for all non-negative integers
in the
range
using an array,
, of size 
.
int sqrt(int x) {
int rp = log(x);
int upgrade = ((r-rp)/2) * 2;
int xp = x << upgrade; // xp has r or r-1 bits
int s = sqrtab[xp>>(r/2)] >> (upgrade/2);
while ((s+1)*(s+1) <= x) s++; // executes at most twice
return s;
}
Something we have taken for granted thus far is the question of how
to compute
. Again, this is a problem that can be solved
with an array,
, of size
. In this case, the
code is particularly simple, since
is just the
index of the most significant 1 bit in the binary representation of
.
This means that, for
, we can right-shift the bits of
by
positions before using it as an index into
.
The following code does this using an array
of size to compute
for all
in the range
int log(int x) {
if (x >= halfint)
return 16 + logtab[x>>16];
return logtab[x];
}
Finally, for completeness, we include the following code that initializes
and
:
void inittabs() {
sqrtab = new int[1<<(r/2)];
logtab = new int[1<<(r/2)];
for (int d = 0; d < r/2; d++)
for (int k = 0; k < 1<<d; k++)
logtab[1<<d+k] = d;
int s = 1<<(r/4); // sqrt(2^(r/2))
for (int i = 0; i < 1<<(r/2); i++) {
if ((s+1)*(s+1) <= i << (r/2)) s++; // sqrt increases
sqrtab[i] = s;
}
}
To summarize, the computations done by the
method can be
implemented in constant time on the word-RAM using
extra
memory to store the
and
arrays. These arrays can be
rebuilt when
increases or decreases by a factor of 2, and the cost
of this rebuilding can be amortized over the number of
and
operations that caused the change in
in the same way that
the cost of
is analyzed in the
implementation.