2.3 $\mathtt{ArrayQueue}$: An Array-Based Queue

In this section, we present the $\mathtt{ArrayQueue}$ data structure, which implements a FIFO (first-in-first-out) queue; elements are removed (using the $\mathtt{remove()}$ operation) from the queue in the same order they are added (using the $\mathtt{add(x)}$ operation).

Notice that an $\mathtt{ArrayStack}$ is a poor choice for an implementation of a FIFO queue. The reason is that we must choose one end of the list to add to and then remove from the other end. One of the two operations must work on the head of the list, which involves calling $\mathtt{add(i,x)}$ or $\mathtt{remove(i)}$ with a value of $\ensuremath{\mathtt{i}}=0$. This gives a running time of $\Theta(n)$.

To obtain an efficient array-based implementation of a queue, we first notice that the problem would be easy if we had an infinite array $\mathtt{a}$. We could maintain one index $\mathtt{j}$ that keeps track of the next element to remove and an integer $\mathtt{n}$ that counts the number of elements in the queue. The queue elements would always be stored in

$$\ensuremath{\mathtt{a[j]}},\ensuremath{\mathtt{a[j+1]}},\ldots,\ensuremath{\mathtt{a[j+n-1]}} \enspace .$$

Initially, both $\mathtt{j}$ and $\mathtt{n}$ would be set to 0. To add an element, we would place it in $\mathtt{a[j+n]}$ and increment $\mathtt{n}$. To remove an element, we would remove it from $\mathtt{a[j]}$, increment $\mathtt{j}$, and decrement $\mathtt{n}$.

Of course, the problem with this solution is that it requires an infinite array. An $\mathtt{ArrayQueue}$ simulates this by using a finite array $\mathtt{a}$ and modular arithmetic. This is the kind of arithmetic used when we are talking about the time of day. For example 10 o'clock plus 5 hours gives 3 o'clock. Formally, we say that

$$10 + 5 = 15 \equiv 3 \pmod{12} \enspace .$$

We read the latter part of this equation as ``15 is congruent to 3 modulo 12.'' We can also treat $\bmod$ as a binary operator, so that

$$15 \bmod 12 = 3 \enspace .$$

More generally, for an integer $a$ and positive integer $m$, $a \bmod m$ is the unique integer $r\in\{0,\ldots,m-1\}$ such that $a = r + km$ for some integer $k$. Less formally, the value $r$ is the remainder we get when we divide $a$ by $m$. In many programming languages, including C++, the $\bmod$ operator is represented using the $\mathtt{\%}$ symbol.²

Modular arithmetic is useful for simulating an infinite array, since $\ensuremath{\mathtt{i}}\bmod \ensuremath{\mathtt{a.length}}$ always gives a value in the range $0,\ldots,\ensuremath{\mathtt{a.length-1}}$. Using modular arithmetic we can store the queue elements at array locations

$$\ensuremath{\mathtt{a[j\%a.length]}},\ensuremath{\mathtt{a[(j+1)\%a.length]}},\ldots,\ensuremath{\mathtt{a[(j+n-1)\%a.length]}} \enspace.$$

This treats $\mathtt{a}$ like a circular array in which array indices exceeding $\ensuremath{\mathtt{a.length}}-1$ ``wrap around'' to the beginning of the array.

The only remaining thing to worry about is taking care that the number of elements in the $\mathtt{ArrayQueue}$ does not exceed the size of $\mathtt{a}$.

  array<T> a;
  int j;
  int n;

A sequence of $\mathtt{add(x)}$ and $\mathtt{remove()}$ operations on an $\mathtt{ArrayQueue}$ is illustrated in Figure 2.2. To implement $\mathtt{add(x)}$, we first check if $\mathtt{a}$ is full and, if necessary, call $\mathtt{resize()}$ to increase the size of $\mathtt{a}$. Next, we store $\mathtt{x}$ in $\mathtt{a[(j+n)\%a.length]}$ and increment $\mathtt{n}$.

Figure 2.2: A sequence of $\mathtt{add(x)}$ and $\mathtt{remove(i)}$ operations on an $\mathtt{ArrayQueue}$. Arrows denote elements being copied. Operations that result in a call to $\mathtt{resize()}$ are marked with an asterisk.

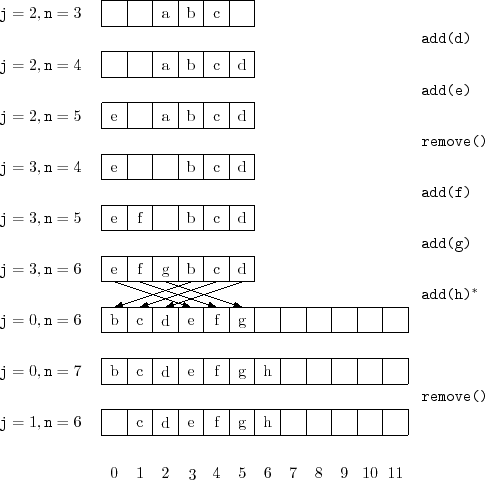
  bool add(T x) {
     if (n + 1 > a.length) resize();
     a[(j+n) % a.length] = x;
     n++;
     return true;
   }

To implement $\mathtt{remove()}$ we first store $\mathtt{a[j]}$ so that we can return it later. Next, we decrement $\mathtt{n}$ and increment $\mathtt{j}$ (modulo $\mathtt{a.length}$) by setting $\ensuremath{\mathtt{j}}=(\ensuremath{\mathtt{j}}+1)\bmod \ensuremath{\mathtt{a.length}}$. Finally, we return the stored value of $\mathtt{a[j]}$. If necessary, we may call $\mathtt{resize()}$ to decrease the size of $\mathtt{a}$.

  T remove() {
    T x = a[j];
    j = (j + 1) % a.length;
    n--;
    if (a.length >= 3*n) resize();
    return x;
  }

Finally, the $\mathtt{resize()}$ operation is very similar to the $\mathtt{resize()}$ operation of $\mathtt{ArrayStack}$. It allocates a new array $\mathtt{b}$ of size $2\ensuremath{\mathtt{n}}$ and copies

$$\ensuremath{\mathtt{a[j]}},\ensuremath{\mathtt{a[(j+1)\%a.length]}},\ldots,\ensuremath{\mathtt{a[(j+n-1)\%a.length]}}$$

onto

$$\ensuremath{\mathtt{b[0]}},\ensuremath{\mathtt{b[1]}},\ldots,\ensuremath{\mathtt{b[n-1]}}$$

and sets $\ensuremath{\mathtt{j}}=0$.

  void resize() {
    array<T> b(max(1, 2*n));
    for (int k = 0; k < n; k++)
      b[k] = a[(j+k)%a.length];
    a = b;
  }

2.3.1 Summary

The following theorem summarizes the performance of the $\mathtt{ArrayQueue}$ data structure:

Theorem 2..2   An $\mathtt{ArrayQueue}$ implements the (FIFO) $\mathtt{Queue}$ interface. Ignoring the cost of calls to $\mathtt{resize()}$, an $\mathtt{ArrayQueue}$ supports the operations $\mathtt{add(x)}$ and $\mathtt{remove()}$ in $O(1)$ time per operation. Furthermore, beginning with an empty $\mathtt{ArrayQueue}$, any sequence of $m$ $\mathtt{add(i,x)}$ and $\mathtt{remove(i)}$ operations results in a total of $O(m)$ time spent during all calls to $\mathtt{resize()}$.

Footnotes

... symbol.²

This is sometimes referred to as the brain-dead mod operator since it does not correctly implement the mathematical mod operator when the first argument is negative.