Next: 2.2 FastArrayStack: An Optimized Up: 2. Array-Based Lists Previous: 2. Array-Based Lists Contents Index
An ArrayStack implements the list interface using an array
, called
the backing array. The list element with index
is stored
in
![$ \ensuremath{\ensuremath{\mathit{a}}[\ensuremath{\mathit{i}}]}$](img471.png){kind=small}
. At most times,
is larger than strictly necessary,
so an integer
is used to keep track of the number of elements
actually stored in
. In this way, the list elements are stored in
![$ \ensuremath{\ensuremath{\mathit{a}}[0]}$](img475.png){kind=small}
,...,
![$ \ensuremath{\ensuremath{\mathit{a}}[\ensuremath{\mathit{n}}-1]}$](img476.png){kind=small}
and, at all times,
.
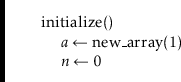
Accessing and modifying the elements of an ArrayStack using
and
is trivial. After performing any necessary bounds-checking
we simply return or set, respectively,
![$ \ensuremath{\ensuremath{\mathit{a}}[\ensuremath{\mathit{i}}]}$](img481.png){kind=small}
.
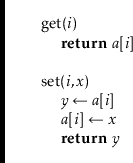
The operations of adding and removing elements from an ArrayStack
are illustrated in Figure 2.1. To implement the
operation, we first check if
is already full. If so, we call
the method
to increase the size of
. How
is implemented will be discussed later. For now, it is sufficient to
know that, after a call to
, we can be sure that
. With this out of the way, we now shift the elements
![$ \ensuremath{\ensuremath{\ensuremath{\mathit{a}}[\ensuremath{\mathit{i}}]}},\ldots,\ensuremath{\ensuremath{\ensuremath{\mathit{a}}[\ensuremath{\mathit{n}}-1]}}$](img490.png){kind=small}
right by one position to make room for
,
set
![$ \ensuremath{\ensuremath{\mathit{a}}[\ensuremath{\mathit{i}}]}$](img492.png){kind=small}
equal to
, and increment
.
![\includegraphics[scale=0.90909]{figs-python/arraystack}](img495.png)
|
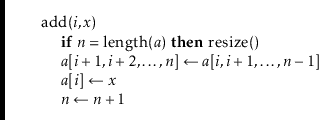
If we ignore the cost of the potential call to
, then the cost
of the
operation is proportional to the number of elements we
have to shift to make room for
. Therefore the cost of this operation
(ignoring the cost of resizing
) is
.
Implementing the
operation is similar. We shift the elements
![$ \ensuremath{\ensuremath{\ensuremath{\mathit{a}}[\ensuremath{\mathit{i}}+1]}},\ldots,\ensuremath{\ensuremath{\ensuremath{\mathit{a}}[\ensuremath{\mathit{n}}-1]}}$](img506.png){kind=small}
left by one position (overwriting
![$ \ensuremath{\ensuremath{\mathit{a}}[\ensuremath{\mathit{i}}]}$](img507.png){kind=small}
) and
decrease the value of
. After doing this, we check if
is getting
much smaller than
by checking if
. If so,
then we call
to reduce the size of
.
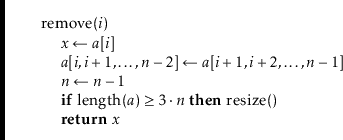
If we ignore the cost of the
method, the cost of a
operation is proportional to the number of elements we shift, which
is
.
The
method is fairly straightforward; it allocates a new
array
whose size is
and copies the
elements of
into
the first
positions in
, and then sets
to
. Thus, after a call to
,
.
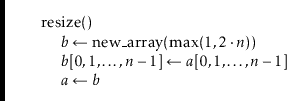
Analyzing the actual cost of the
operation is easy. It
allocates an array
of size
and copies the
elements of
into
. This takes
time.
The running time analysis from the previous section ignored the cost
of calls to
. In this section we analyze this cost using a
technique known as amortized analysis. This technique does not
try to determine the cost of resizing during each individual
and
operation. Instead, it considers the cost of all calls to
during a sequence of 
calls to
or
.
In particular, we will show:
calls
to
and
are performed, then the total time spent
during all calls to
is 
.
is called, the number of calls
to
or
since the last call to
is at least
. Therefore, if
denotes the value of
during the
th call to
and 
denotes the number of calls to
, then the total number of calls to
or
is at least
is
is not more than 
. All that remains is to show that the
number of calls to
or
between the 
th
and the 
th call to
is at least
.
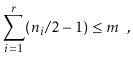
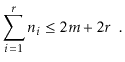
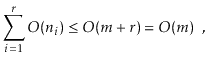
There are two cases to consider. In the first case,
is
being called by
because the backing array
is full, i.e.,
. Consider the previous call to
:
after this previous call, the size of
was
, but the
number of elements stored in
was at most
.
But now the number of elements stored in
is
,
so there must have been at least
calls to
since
the previous call to
.
The second case occurs when
is being called by
because
. Again, after the
previous call to
the number of elements stored in
was
at least
.2.1 Now there
are
elements stored in
. Therefore, the number
of
operations since the last call to
is at least
 |
 |
|
 |
||
 |
||
 |
or
that
occur between the 
th call to
and the 
th call to
is at least
, as required to complete the proof.
The following theorem summarizes the performance of an ArrayStack:
, an ArrayStack supports the operations
and
in 
time per operation; and
and
in
time per operation.
and
operations results in a
total of 
time spent during all calls to
.
The ArrayStack is an efficient way to implement a Stack.
In particular, we can implement
as
and
as
, in which case these operations will run in 
amortized time.
in this formula accounts for
the special case that occurs when
and
.
