Subsections

2.6 RootishArrayStack: A Space-Efficient Array Stack

One of the drawbacks of all previous data structures in this chapter is that, because they store their data in one or two arrays and they avoid resizing these arrays too often, the arrays frequently are not very full. For example, immediately after a $\ensuremath{\mathrm{resize}()}$ operation on an ArrayStack, the backing array $\ensuremath{\ensuremath{\mathit{a}}}$ is only half full. Even worse, there are times when only one third of $\ensuremath{\ensuremath{\mathit{a}}}$ contains data.

In this section, we discuss the RootishArrayStack data structure, that addresses the problem of wasted space. The RootishArrayStack stores $\ensuremath{\ensuremath{\mathit{n}}}$ elements using $O(\sqrt{\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}})$ arrays. In these arrays, at most $O(\sqrt{\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}})$ array locations are unused at any time. All remaining array locations are used to store data. Therefore, these data structures waste at most $O(\sqrt{\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}})$ space when storing $\ensuremath{\ensuremath{\mathit{n}}}$ elements.

A RootishArrayStack stores its elements in a list of $\ensuremath{\ensuremath{\mathit{r}}}$ arrays called blocks that are numbered $0,1,\ldots,\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}}-1$ . See Figure 2.5. Block contains elements. Therefore, all $\ensuremath{\ensuremath{\mathit{r}}}$ blocks contain a total of

$\displaystyle 1+ 2+ 3+\cdots +\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}}... ...nsuremath{\mathit{r}}}}(\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}}+1)/2$

elements. The above formula can be obtained as shown in Figure 2.6.

**Figure 2.5:** A sequence of $\ensuremath{\mathrm{add}(\ensuremath{\mathit{i}},\ensuremath{\mathit{x}})}$ and $\ensuremath{\mathrm{remove}(\ensuremath{\mathit{i}})}$ operations on a RootishArrayStack. Arrows denote elements being copied.
$\includegraphics[width=\textwidth ]{figs-python/rootisharraystack}$

$\begin{leftbar} \begin{flushleft} \hspace*{1em} \ensuremath{\mathrm{initialize}(... ...ets \ensuremath{\mathrm{\mathrm{ArrayStack}}()}}\\ \end{flushleft}\end{leftbar}$

**Figure 2.6:** The number of white squares is $1+2+3+\cdots+\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}}$ . The number of shaded squares is the same. Together the white and shaded squares make a rectangle consisting of $\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}}(\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}}+1)$ squares.
$\includegraphics[scale=0.90909]{figs-python/gauss}$

As we might expect, the elements of the list are laid out in order within the blocks. The list element with index 0 is stored in block 0, elements with list indices 1 and 2 are stored in block 1, elements with list indices 3, 4, and 5 are stored in block 2, and so on. The main problem we have to address is that of determining, given an index $\ensuremath{\ensuremath{\ensuremath{\mathit{i}}}}$ , which block contains $\ensuremath{\ensuremath{\mathit{i}}}$ as well as the index corresponding to $\ensuremath{\ensuremath{\mathit{i}}}$ within that block.

Determining the index of $\ensuremath{\ensuremath{\mathit{i}}}$ within its block turns out to be easy. If index $\ensuremath{\ensuremath{\mathit{i}}}$ is in block $\ensuremath{\ensuremath{\mathit{b}}}$ , then the number of elements in blocks $0,\ldots,\ensuremath{\ensuremath{\ensuremath{\mathit{b}}}}-1$ is $\ensuremath{\ensuremath{\ensuremath{\mathit{b}}}}(\ensuremath{\ensuremath{\ensuremath{\mathit{b}}}}+1)/2$ . Therefore, $\ensuremath{\ensuremath{\mathit{i}}}$ is stored at location

$\displaystyle \ensuremath{\ensuremath{\ensuremath{\mathit{j}}}} = \ensuremath{\... ...nsuremath{\mathit{b}}}}(\ensuremath{\ensuremath{\ensuremath{\mathit{b}}}}+1)/2$

within block $\ensuremath{\ensuremath{\mathit{b}}}$ . Somewhat more challenging is the problem of determining the value of $\ensuremath{\ensuremath{\mathit{b}}}$ . The number of elements that have indices less than or equal to $\ensuremath{\ensuremath{\mathit{i}}}$ is $\ensuremath{\ensuremath{\ensuremath{\mathit{i}}}}+1$ . On the other hand, the number of elements in blocks 0,...,b is $(\ensuremath{\ensuremath{\ensuremath{\mathit{b}}}}+1)(\ensuremath{\ensuremath{\ensuremath{\mathit{b}}}}+2)/2$ . Therefore, $\ensuremath{\ensuremath{\mathit{b}}}$ is the smallest integer such that

$\displaystyle (\ensuremath{\ensuremath{\ensuremath{\mathit{b}}}}+1)(\ensuremath... ...{b}}}}+2)/2 \ge \ensuremath{\ensuremath{\ensuremath{\mathit{i}}}}+1 \enspace .$

We can rewrite this equation as

$\displaystyle \ensuremath{\ensuremath{\ensuremath{\mathit{b}}}}^2 + 3\ensuremat... ...it{b}}}} - 2\ensuremath{\ensuremath{\ensuremath{\mathit{i}}}} \ge 0 \enspace .$

The corresponding quadratic equation $\ensuremath{\ensuremath{\ensuremath{\mathit{b}}}}^2 + 3\ensuremath{\ensuremath... ...suremath{\mathit{b}}}} - 2\ensuremath{\ensuremath{\ensuremath{\mathit{i}}}} = 0$ has two solutions: $\ensuremath{\ensuremath{\ensuremath{\mathit{b}}}}=(-3 + \sqrt{9+8\ensuremath{\ensuremath{\ensuremath{\mathit{i}}}}}) / 2$ and $\ensuremath{\ensuremath{\ensuremath{\mathit{b}}}}=(-3 - \sqrt{9+8\ensuremath{\ensuremath{\ensuremath{\mathit{i}}}}}) / 2$ . The second solution makes no sense in our application since it always gives a negative value. Therefore, we obtain the solution $\ensuremath{\ensuremath{\ensuremath{\mathit{b}}}} = (-3 + \sqrt{9+8i}) / 2$ . In general, this solution is not an integer, but going back to our inequality, we want the smallest integer $\ensuremath{\ensuremath{\ensuremath{\mathit{b}}}}$ such that $\ensuremath{\ensuremath{\ensuremath{\mathit{b}}}} \ge (-3 + \sqrt{9+8i}) / 2$ . This is simply

$\displaystyle \ensuremath{\ensuremath{\ensuremath{\mathit{b}}}} = \left\lceil(-3 + \sqrt{9+8i}) / 2\right\rceil \enspace .$

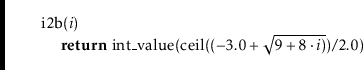
$\begin{leftbar} \begin{flushleft} \hspace*{1em} \ensuremath{\mathrm{i2b}(\ensure... ... \ensuremath{\mathit{i}})}) / \ensuremath{2.0})}\\ \end{flushleft}\end{leftbar}$

With this out of the way, the $\ensuremath{\mathrm{get}(\ensuremath{\mathit{i}})}$ and $\ensuremath{\mathrm{set}(\ensuremath{\mathit{i}},\ensuremath{\mathit{x}})}$ methods are straightforward. We first compute the appropriate block $\ensuremath{\ensuremath{\mathit{b}}}$ and the appropriate index $\ensuremath{\ensuremath{\mathit{j}}}$ within the block and then perform the appropriate operation:

$\begin{leftbar} \begin{flushleft} \hspace*{1em} \ensuremath{\mathrm{get}(\ensure... ...bf{return}} \ensuremath{\ensuremath{\mathit{y}}}\\ \end{flushleft}\end{leftbar}$

If we use any of the data structures in this chapter for representing the $\ensuremath{\ensuremath{\mathit{blocks}}}$ list, then $\ensuremath{\mathrm{get}(\ensuremath{\mathit{i}})}$ and $\ensuremath{\mathrm{set}(\ensuremath{\mathit{i}},\ensuremath{\mathit{x}})}$ will each run in constant time.

The $\ensuremath{\mathrm{add}(\ensuremath{\mathit{i}},\ensuremath{\mathit{x}})}$ method will, by now, look familiar. We first check to see if our data structure is full, by checking if the number of blocks, $\ensuremath{\ensuremath{\mathit{r}}}$ , is such that $\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}}(\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}}+1)/2 = \ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}$ . If so, we call $\ensuremath{\mathrm{grow}()}$ to add another block. With this done, we shift elements with indices $\ensuremath{\ensuremath{\ensuremath{\mathit{i}}}},\ldots,\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}-1$ to the right by one position to make room for the new element with index $\ensuremath{\ensuremath{\mathit{i}}}$ :

$\begin{leftbar} \begin{flushleft} \hspace*{1em} \ensuremath{\mathrm{add}(\ensure... ...nsuremath{\mathit{i}}, \ensuremath{\mathit{x}})}\\ \end{flushleft}\end{leftbar}$

The $\ensuremath{\mathrm{grow}()}$ method does what we expect. It adds a new block:

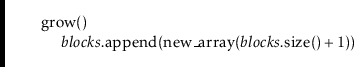
$\begin{leftbar} \begin{flushleft} \hspace*{1em} \ensuremath{\mathrm{grow}()}\\ ... ...ensuremath{\mathit{blocks}}.\mathrm{size}()+1}))\\ \end{flushleft}\end{leftbar}$

Ignoring the cost of the $\ensuremath{\mathrm{grow}()}$ operation, the cost of an $\ensuremath{\mathrm{add}(\ensuremath{\mathit{i}},\ensuremath{\mathit{x}})}$ operation is dominated by the cost of shifting and is therefore $O(1+\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}-\ensuremath{\ensuremath{\ensuremath{\mathit{i}}}})$ , just like an ArrayStack.

The $\ensuremath{\mathrm{remove}(\ensuremath{\mathit{i}})}$ operation is similar to $\ensuremath{\mathrm{add}(\ensuremath{\mathit{i}},\ensuremath{\mathit{x}})}$ . It shifts the elements with indices $\ensuremath{\ensuremath{\ensuremath{\mathit{i}}}}+1,\ldots,\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}$ left by one position and then, if there is more than one empty block, it calls the $\ensuremath{\mathrm{shrink}()}$ method to remove all but one of the unused blocks:

$\begin{leftbar} \begin{flushleft} \hspace*{1em} \ensuremath{\mathrm{remove}(\ens... ...bf{return}} \ensuremath{\ensuremath{\mathit{x}}}\\ \end{flushleft}\end{leftbar}$

$\begin{leftbar} \begin{flushleft} \hspace*{1em} \ensuremath{\mathrm{shrink}()}\\... ... \gets \ensuremath{\ensuremath{\mathit{r}} - 1}}\\ \end{flushleft}\end{leftbar}$

Once again, ignoring the cost of the $\ensuremath{\mathrm{shrink}()}$ operation, the cost of a $\ensuremath{\mathrm{remove}(\ensuremath{\mathit{i}})}$ operation is dominated by the cost of shifting and is therefore $O(\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}-\ensuremath{\ensuremath{\ensuremath{\mathit{i}}}})$ .

2.6.1 Analysis of Growing and Shrinking

The above analysis of $\ensuremath{\mathrm{add}(\ensuremath{\mathit{i}},\ensuremath{\mathit{x}})}$ and $\ensuremath{\mathrm{remove}(\ensuremath{\mathit{i}})}$ does not account for the cost of $\ensuremath{\mathrm{grow}()}$ and $\ensuremath{\mathrm{shrink}()}$ . Note that, unlike the $\ensuremath{\mathrm{ArrayStack}.\mathrm{resize}()}$ operation, $\ensuremath{\mathrm{grow}()}$ and $\ensuremath{\mathrm{shrink}()}$ do not copy any data. They only allocate or free an array of size $\ensuremath{\ensuremath{\mathit{r}}}$ . In some environments, this takes only constant time, while in others, it may require time proportional to $\ensuremath{\ensuremath{\mathit{r}}}$ .

We note that, immediately after a call to $\ensuremath{\mathrm{grow}()}$ or $\ensuremath{\mathrm{shrink}()}$ , the situation is clear. The final block is completely empty, and all other blocks are completely full. Another call to $\ensuremath{\mathrm{grow}()}$ or $\ensuremath{\mathrm{shrink}()}$ will not happen until at least $\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}}-1$ elements have been added or removed. Therefore, even if $\ensuremath{\mathrm{grow}()}$ and $\ensuremath{\mathrm{shrink}()}$ take $O(\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}})$ time, this cost can be amortized over at least $\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}}-1$ $\ensuremath{\mathrm{add}(\ensuremath{\mathit{i}},\ensuremath{\mathit{x}})}$ or $\ensuremath{\mathrm{remove}(\ensuremath{\mathit{i}})}$ operations, so that the amortized cost of $\ensuremath{\mathrm{grow}()}$ and $\ensuremath{\mathrm{shrink}()}$ is per operation.

2.6.2 Space Usage

Next, we analyze the amount of extra space used by a RootishArrayStack. In particular, we want to count any space used by a RootishArrayStack that is not an array element currently used to hold a list element. We call all such space wasted space.

The $\ensuremath{\mathrm{remove}(\ensuremath{\mathit{i}})}$ operation ensures that a RootishArrayStack never has more than two blocks that are not completely full. The number of blocks, $\ensuremath{\ensuremath{\mathit{r}}}$ , used by a RootishArrayStack that stores $\ensuremath{\ensuremath{\mathit{n}}}$ elements therefore satisfies

$\displaystyle (\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}}-2)(\ensuremath... ...thit{r}}}}-1) \le \ensuremath{\ensuremath{\ensuremath{\mathit{n}}}} \enspace .$

Again, using the quadratic equation on this gives

$\displaystyle \ensuremath{\ensuremath{\ensuremath{\mathit{r}}}} \le (3+\sqrt{1+... ...}})/2 = O(\sqrt{\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}}) \enspace .$

The last two blocks have sizes $\ensuremath{\ensuremath{\mathit{r}}}$ and $\ensuremath{\ensuremath{\mathit{r}}-1}$ , so the space wasted by these two blocks is at most $2\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}}-1 = O(\sqrt{\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}})$ . If we store the blocks in (for example) an ArrayStack, then the amount of space wasted by the List that stores those $\ensuremath{\ensuremath{\mathit{r}}}$ blocks is also $O(\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}})=O(\sqrt{\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}})$ . The other space needed for storing $\ensuremath{\ensuremath{\mathit{n}}}$ and other accounting information is

. Therefore, the total amount of wasted space in a RootishArrayStack is $O(\sqrt{\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}})$ .

Next, we argue that this space usage is optimal for any data structure that starts out empty and can support the addition of one item at a time. More precisely, we will show that, at some point during the addition of $\ensuremath{\ensuremath{\mathit{n}}}$ items, the data structure is wasting an amount of space at least in $\sqrt{\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}}$ (though it may be only wasted for a moment).

Suppose we start with an empty data structure and we add $\ensuremath{\ensuremath{\mathit{n}}}$ items one at a time. At the end of this process, all $\ensuremath{\ensuremath{\mathit{n}}}$ items are stored in the structure and distributed among a collection of $\ensuremath{\ensuremath{\mathit{r}}}$ memory blocks. If $\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}}\ge \sqrt{\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}}$ , then the data structure must be using $\ensuremath{\ensuremath{\mathit{r}}}$ pointers (or references) to keep track of these $\ensuremath{\ensuremath{\mathit{r}}}$ blocks, and these pointers are wasted space. On the other hand, if $\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}} < \sqrt{\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}}$ then, by the pigeonhole principle, some block must have a size of at least $\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}/\ensuremath{\ensuremath{\ensuremath{\mathit{r}}}} > \sqrt{\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}}$ . Consider the moment at which this block was first allocated. Immediately after it was allocated, this block was empty, and was therefore wasting $\sqrt{\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}}$ space. Therefore, at some point in time during the insertion of $\ensuremath{\ensuremath{\mathit{n}}}$ elements, the data structure was wasting $\sqrt{\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}}$ space.

2.6.3 Summary

The following theorem summarizes our discussion of the RootishArrayStack data structure:

Theorem 2..5 A RootishArrayStack implements the List interface. Ignoring the cost of calls to $\ensuremath{\mathrm{grow}()}$ and $\ensuremath{\mathrm{shrink}()}$ , a RootishArrayStack supports the operations

$\ensuremath{\mathrm{get}(\ensuremath{\mathit{i}})}$ and $\ensuremath{\mathrm{set}(\ensuremath{\mathit{i}},\ensuremath{\mathit{x}})}$ in time per operation; and
$\ensuremath{\mathrm{add}(\ensuremath{\mathit{i}},\ensuremath{\mathit{x}})}$ and $\ensuremath{\mathrm{remove}(\ensuremath{\mathit{i}})}$ in $O(1+\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}-\ensuremath{\ensuremath{\ensuremath{\mathit{i}}}})$ time per operation.

Furthermore, beginning with an empty RootishArrayStack, any sequence of $\ensuremath{\mathrm{add}(\ensuremath{\mathit{i}},\ensuremath{\mathit{x}})}$ and $\ensuremath{\mathrm{remove}(\ensuremath{\mathit{i}})}$ operations results in a total of time spent during all calls to $\ensuremath{\mathrm{grow}()}$ and $\ensuremath{\mathrm{shrink}()}$ .

The space (measured in words)^2.2 used by a RootishArrayStack that stores $\ensuremath{\ensuremath{\mathit{n}}}$ elements is $\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}} +O(\sqrt{\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}})$ .

Footnotes

... words)^2.2: Recall Section 1.4 for a discussion of how memory is measured.

opendatastructures.org