1.1 Interfaces

In discussing data structures, it is important to understand the difference between a data structure's interface and its implementation. An interface describes what a data structure does, while an implementation describes how the data structure does it.

An interface, sometimes also called an abstract data type, defines the set of operations supported by a data structure and the semantics, or meaning, of those operations. An interface tells us nothing about how the data structure implements these operations, it only provides the list of supported operations along with specifications about what types of arguments each operation accepts and the value returned by each operation.

A data structure implementation on the other hand, includes the internal representation of the data structure as well as the definitions of the algorithms that implement the operations supported by the data structure. Thus, there can be many implementations of a single interface. For example, in Chapter 2, we will see implementations of the List interface using arrays and in Chapter 3 we will see implementations of the List interface using pointer-based data structures. Each implements the same interface, List, but in different ways.

1.1.1 The Queue, Stack, and Deque Interfaces

The Queue interface represents a collection of elements to which we can add elements and remove the next element. More precisely, the operations supported by the Queue interface are

• $\mathtt{add(x)}$: add the value $\mathtt{x}$ to the Queue
• $\mathtt{remove()}$: remove the next (previously added) value, $\mathtt{y}$, from the Queue and return $\mathtt{y}$

Notice that the $\mathtt{remove()}$ operation takes no argument. The Queue's queueing discipline decides which element should be removed. There are many possible queueing disciplines, the most common of which include FIFO, priority, and LIFO.

A FIFO (first-in-first-out) Queue, illustrated in Figure 1.1, removes items in the same order they were added, much in the same way a queue (or line-up) works when checking out at a cash register in a grocery store. This is the most common kind of Queue so the qualifier FIFO is often ommitted. In other texts, the $\mathtt{add(x)}$ and $\mathtt{remove()}$ operations on a FIFO Queue are often called $\mathtt{enqueue(x)}$ and $\mathtt{dequeue()}$, respectively.

Figure 1.1: A FIFO Queue.

A priority Queue, illustrated in Figure 1.2, always removes the smallest element from the Queue, breaking ties arbitrarily. This is similar to the way patients are triaged in a hospital emergency room. As patients arrive they are evaluated and then placed in a waiting room. When a doctor becomes available they first treat the patient with the most life-threatening condition. The $\mathtt{remove(x)}$ operation on a priority Queue is usually called $\mathtt{deleteMin()}$ in other texts.

Figure 1.2: A priority Queue.

A very common queueing discipline is the LIFO (last-in-first-out) discipline, illustrated in Figure 1.3. In a LIFO Queue, the most recently added element is the next one removed. This is best visualized in terms of a stack of plates; plates are placed on the top of the stack and also removed from the top of the stack. This structure is so common that it gets its own name: Stack. Often, when discussing a Stack, the names of $\mathtt{add(x)}$ and $\mathtt{remove()}$ are changed to $\mathtt{push(x)}$ and $\mathtt{pop()}$; this is to avoid confusing the LIFO and FIFO queueing disciplines.

Figure 1.3: A stack.

A Deque is a generalization of both the FIFO Queue and LIFO Queue (Stack). A Deque represents a sequence of elements, with a front and a back. Elements can be added at the front of the sequence or the back of the sequence. The names of the operations on a Deque are self-explanatory: $\mathtt{addFirst(x)}$, $\mathtt{removeFirst()}$, $\mathtt{addLast(x)}$, and $\mathtt{removeLast()}$. Notice that a Stack can be implemented using only $\mathtt{addFirst(x)}$ and $\mathtt{removeFirst()}$ while a FIFO Queue can be implemented using only $\mathtt{addLast(x)}$ and $\mathtt{removeFirst()}$.

1.1.2 The List Interface: Linear Sequences

This book will talk very little about the FIFO Queue, Stack, or Deque interfaces. This is because these interfaces are subsumed by the List interface. A List, illustrated in Figure 1.4, represents a sequence, $\ensuremath{\mathtt{x}}_0,\ldots,\ensuremath{\mathtt{x}}_{\ensuremath{\mathtt{n}}-1}$, of values. The List interface includes the following operations:

1. $\mathtt{size()}$: return $\mathtt{n}$, the length of the list
2. $\mathtt{get(i)}$: return the value $\ensuremath{\mathtt{x}}_{\ensuremath{\mathtt{i}}}$
3. $\mathtt{set(i,x)}$: set the value of $\ensuremath{\mathtt{x}}_{\ensuremath{\mathtt{i}}}$ equal to $\mathtt{x}$
4. $\mathtt{add(i,x)}$: add $\mathtt{x}$ at position $\mathtt{i}$, displacing $\ensuremath{\mathtt{x}}_{\ensuremath{\mathtt{i}}},\ldots,\ensuremath{\mathtt{x}}_{\ensuremath{\mathtt{n}}-1}$;
   Set $\ensuremath{\mathtt{x}}_{j+1}=\ensuremath{\mathtt{x}}_j$, for all $j\in\{\ensuremath{\mathtt{n}}-1,\ldots,\ensuremath{\mathtt{i}}\}$, increment $\mathtt{n}$, and set $\ensuremath{\mathtt{x}}_i=\ensuremath{\mathtt{x}}$
5. $\mathtt{remove(i)}$ remove the value $\ensuremath{\mathtt{x}}_{\ensuremath{\mathtt{i}}}$, displacing $\ensuremath{\mathtt{x}}_{\ensuremath{\mathtt{i+1}}},\ldots,\ensuremath{\mathtt{x}}_{\ensuremath{\mathtt{n}}-1}$;
   Set $\ensuremath{\mathtt{x}}_{j}=\ensuremath{\mathtt{x}}_{j+1}$, for all $j\in\{\ensuremath{\mathtt{i}},\ldots,\ensuremath{\mathtt{n}}-2\}$ and decrement $\mathtt{n}$

Notice that these operations are easily sufficient to implement the Deque interface:

$$\ensuremath{\mathtt{addFirst(x)}} \Rightarrow \ensuremath{\mathtt{add(0,x)}}$$

$$\ensuremath{\mathtt{removeFirst()}} \Rightarrow \ensuremath{\mathtt{remove(0)}}$$

$$\ensuremath{\mathtt{addLast(x)}} \Rightarrow \ensuremath{\mathtt{add(size(),x)}}$$

$$\ensuremath{\mathtt{removeLast()}} \Rightarrow \ensuremath{\mathtt{remove(size()-1)}}$$

Figure 1.4: A List represents a sequence indexed by $0,1,2,\ldots,\ensuremath{\mathtt{n}}$. In this List a call to $\mathtt{get(2)}$ would return the value $c$.

Although we will normally not discuss the Stack, Deque and FIFO Queue interfaces in subsequent chapters, the terms Stack and Deque are sometimes used in the names of data structures that implement the List interface. When this happens, it is to highlight the fact that these data structures can be used to implement the Stack or Deque interface very efficiently. For example, the ArrayDeque class is an implementation of the List interface that implements all the Deque operations in constant time per operation.

1.1.3 The USet Interface: Unordered Sets

The USet interface represents an unordered set of unique elements, mimicking a mathematical set. A USet contains $\mathtt{n}$ distinct elements; no element appears more than once; the elements are in no specific order. A USet supports the following operations:

1. $\mathtt{size()}$: return the number, $\mathtt{n}$, of elements in the set
2. $\mathtt{add(x)}$: add the element $\mathtt{x}$ to the set if not already present;
   Add $\mathtt{x}$ to the set provided that there is no element $\mathtt{y}$ in the set such that $\mathtt{x}$ equals $\mathtt{y}$. Return $\mathtt{true}$ if $\mathtt{x}$ was added to the set and $\mathtt{false}$ otherwise.
3. $\mathtt{remove(x)}$: remove $\mathtt{x}$ from the set;
   Find an element $\mathtt{y}$ in the set such that $\mathtt{x}$ equals $\mathtt{y}$ and remove $\mathtt{y}$. Return $\mathtt{y}$, or $\mathtt{null}$ if no such element exists.
4. $\mathtt{find(x)}$: find $\mathtt{x}$ in the set if it exists;
   Find an element $\mathtt{y}$ in the set such that $\mathtt{y}$ equals $\mathtt{x}$. Return $\mathtt{y}$, or $\mathtt{null}$ if no such element exists.

These definitions are a bit fussy about distinguishing $\mathtt{x}$, the element we are removing or finding, from $\mathtt{y}$, the element we remove or find. This is because $\mathtt{x}$ and $\mathtt{y}$ might actually be distinct objects that are nevertheless treated as equal.^1.2This is a very useful distinction since it allows for the creation of dictionaries or maps that map keys onto values. This is done by creating a compound object called a Pair that contains a key and a value. Two Pairs are treated as equal if their keys are equal. By storing Pairs in a USet, we can find the value associated with any key $\mathtt{k}$ by creating a Pair, $\mathtt{x}$, with key $\mathtt{k}$ and using the $\mathtt{find(x)}$ method.

1.1.4 The SSet Interface: Sorted Sets

The SSet interface represents a sorted set of elements. An SSet stores elements from some total order, so that any two elements $\mathtt{x}$ and $\mathtt{y}$ can be compared. In code examples, this will be done with a method called $\mathtt{compare(x,y)}$ in which

$$\ensuremath{\mathtt{compare(x,y)}} \begin{cases} {}<0 & \text{... ...{}=0 & \text{if $\ensuremath{\mathtt{x}}=\ensuremath{\mathtt{y}}$} \end{cases}$$

An SSet supports the $\mathtt{size()}$, $\mathtt{add(x)}$, and $\mathtt{remove(x)}$ methods with exactly the same semantics as in the USet interface. The difference between a USet and an SSet is in the $\mathtt{find(x)}$ method:

1. $\mathtt{find(x)}$: locate $\mathtt{x}$ in the sorted set;
   Find the smallest element $\mathtt{y}$ in the set such that $\ensuremath{\mathtt{y}} \ge \ensuremath{\mathtt{x}}$. Return $\mathtt{y}$ or $\mathtt{null}$ if no such element exists.

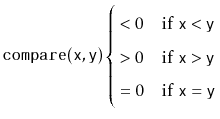
This version of the $\mathtt{find(x)}$ operation is sometimes referred to as a successor search. It differs in a fundamental way from $\mathtt{USet.find(x)}$ since it returns a meaningful result even when there is no element in the set that is equal to $\mathtt{x}$.

The distinction between the USet and SSet $\mathtt{find(x)}$ operations is very important and is very often missed. The extra functionality provided by an SSet usually comes with a price that includes both a larger running time and a higher implementation complexity. For example, most of the SSet implementations discussed in this book all have $\mathtt{find(x)}$ operations with running times that are logarithmic in the size of the set. On the other hand, the implementation of a USet as a ChainedHashTable in Chapter 5 has a $\mathtt{find(x)}$ operation that runs in constant expected time. When choosing which of these structures to use, one should always use a USet unless the extra functionality offered by an SSet is really needed.

Footnotes

... equal.^1.2

In Java, this is done by overriding the class' $\mathtt{equals(y)}$ and $\mathtt{hashCode()}$ methods.