Both singly-linked and doubly-linked lists are folklore, having been
used in programs for over 40 years. They are discussed, for example,
by Knuth [41, Sections 2.2.3-2.2.5]. Even the
 data
structure seems to be a well-known data structures exercise.
data
structure seems to be a well-known data structures exercise.
Exercise 3..1
Why is it not possible, in an
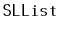
to use a dummy node to avoid
all the special cases that occur in the operations
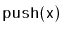
,
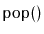
,
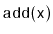
, and
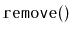
?
Exercise 3..2
Design and implement an
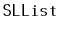
method,
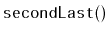
, that returns
the second-last element of an
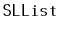
. Do this without using the
member variable,
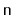
, that keeps track of the size of the list.
Exercise 3..3
Describe and implement the

operations
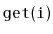
,
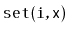
,
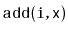
and
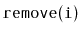
on an
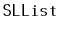
. Each of these operations
should run in
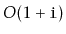
time.
Exercise 3..4
Design and implement an
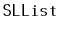
method,
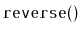
that reverses the
order of elements in an
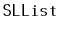
. This method should run in
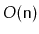
time, should not use recursion, should not use any secondary data
structures, and should not create any new nodes.
Exercise 3..5
Design and implement
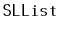
and
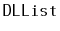
methods called
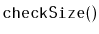
.
These methods walk through the list and count the number of nodes to
see if this matches the value,
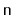
, stored in the list. These methods
return nothing, but throw an exception if the size they compute does
not match the value of
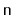
.
Exercise 3..6
Without referring to this chapter, try to recreate the code for the

operation, that creates a node,
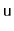
, and adds it just
before the node
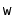
in a
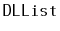
. If your code does not exactly match
the code given in this book it may still be correct. Test it and see
if it works.
The next few exercises involve performing manipulations on
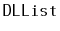 s.
These should all be done without allocating any new nodes or temporary
arrays. More specifically, they can all be done only by changing
the
s.
These should all be done without allocating any new nodes or temporary
arrays. More specifically, they can all be done only by changing
the
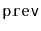 and
and
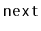 values of existing nodes.
values of existing nodes.
Exercise 3..7
Write a
method

that returns

if the
list is a palindrome, i.e., the element at position
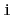
is equal to
the element at position
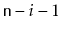
for all
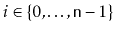
.
Your code should run in
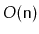
time.
Exercise 3..8
Implement a method

that ``rotates'' a
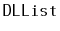
so that list
item
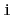
becomes list item
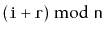
. This method should
run in
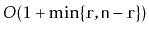
time and should not modify any nodes in
the list.
Exercise 3..9
Write a method,
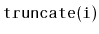
, that truncates a
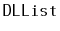
at position
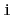
. After the execution of this method, the size of the list is
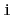
and it contains only the elements at indices
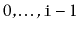
. The
return value is another
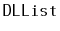
that contains the elements at indices
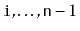
. This method should run in
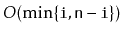
time.
Exercise 3..10
Write a
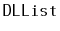
method,
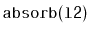
, that takes as an argument
a
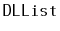
,
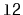
, empties it and appends its contents, in order,
to the receiver. For example, if
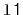
contains
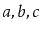
and
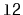
contains
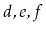
, then after calling
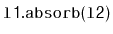
,
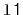
will contain
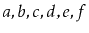
and
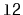
will be empty.
Exercise 3..11
Write a method
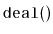
that removes all the elements with odd-numbered
indices from a
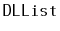
and return a
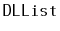
containing these elements.
For example, if
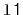
, contains the elements
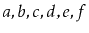
, then after
calling
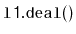
,
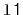
should contain
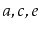
and a list containing
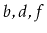
should be returned.
Exercise 3..12
Write a method,
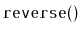
, that reverses the order of elements in
a
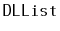
.
Exercise 3..13
This exercises walks you through an implementation of the merge sort
algorithm for sorting a
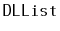
, as discussed in Section
11.1.1.
- Write a
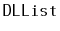 method called
method called
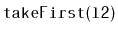 .
This method takes the first node from
.
This method takes the first node from
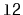 and appends it to the the
receiving list. This is equivalent to
and appends it to the the
receiving list. This is equivalent to
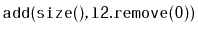 ,
except that it should not create a new node.
,
except that it should not create a new node.
- Write a
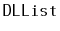 static method,
static method,
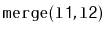 , that takes two
sorted lists
, that takes two
sorted lists
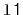 and
and
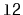 , merges them, and returns a new sorted
list containing the result. This causes
, merges them, and returns a new sorted
list containing the result. This causes
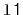 and
and
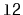 to be emptied
in the proces. For example, if
to be emptied
in the proces. For example, if
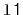 contains
contains 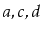 and
and
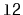 contains
contains
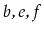 , then this method returns a new list containing
, then this method returns a new list containing
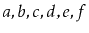 .
.
- Write a
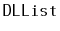 method
method
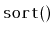 that sorts the elements contained
in the list using the merge sort algorithm. This recursive algorithm works as following:
that sorts the elements contained
in the list using the merge sort algorithm. This recursive algorithm works as following:
- If the list contains 0 or 1 elements then there is
nothing to do. Otherwise,
- Split the list into two approximately equal length lists
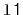 and
and
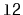 using the
using the
 method;
method;
- Recursively sort
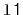 ;
;
- Recursively sort
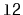 ; and, finally,
; and, finally,
- Merge
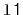 and
and
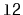 into a single sorted list.
into a single sorted list.
The next few exercises are more advanced and require a clear
understanding of what happens to the minimum value stored in a
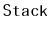 or
or
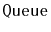 as items are added and removed.
as items are added and removed.
Exercise 3..14
Design and implement a
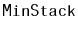
data structure that can store
comparable elements and supports the stack operations
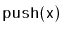
,
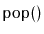
, and
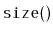
, as well as the
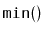
operation, which
returns the minimum value currently stored in the data structure.
All operations should run in constant time.
Exercise 3..15
Design an implement a
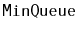
data structure that can store
comparable elements and supports the queue operations
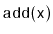
,
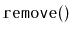
, and
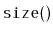
, as well as the
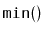
operation, which
returns the minimum value currently stored in the data structure.
All operations should run in constant amortized time.
Exercise 3..16
Design an implement a
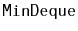
data structure that can store
comparable elements and supports the queue operations
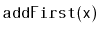
,
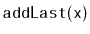
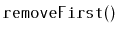
,

and
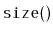
, as well
as the
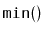
operation, which returns the minimum value currently
stored in the data structure. All operations should run in constant
amortized time.
The next exercises are designed to test the reader's understanding of
the implementation an analysis of the space-efficient
 :
:
Exercise 3..17
Prove that, if an

is used like a
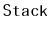
(so that the
modifications are done using
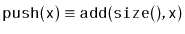
and

) then these operations run in
constant amortized time, independent of the value of
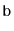
.
Exercise 3..18
Design an implement of a version of an

that supports all
the
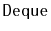
operations in constant amortized time per operation,
independent of the value of
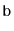
.
opendatastructures.org
![]() data
structure seems to be a well-known data structures exercise.
data
structure seems to be a well-known data structures exercise.
![]() s.
These should all be done without allocating any new nodes or temporary
arrays. More specifically, they can all be done only by changing
the
s.
These should all be done without allocating any new nodes or temporary
arrays. More specifically, they can all be done only by changing
the
![]() and
and
![]() values of existing nodes.
values of existing nodes.
![]() or
or
![]() as items are added and removed.
as items are added and removed.
![]() :
: