Next: 11.2 Counting Sort and Up: 11. Sorting Algorithms Previous: 11. Sorting Algorithms Contents
In this section, we present three sorting algorithms: merge-sort,
quicksort, and heap-sort. All these algorithms take an input array
and sort the elements of
into non-decreasing order in
(expected) time. These algorithms are all comparison-based.
Their second argument,
, is a Comparator that implements
the
method. These algorithms don't care what type
of data is being sorted, the only operation they do on the data is
comparisons using the
method. Recall, from ,
that
returns a negative value if
, a positive
value if
, and zero if
.
The merge-sort algorithm is a classic example of recursive divide
and conquer: If the length of
is at most 1, then
is already
sorted, so we do nothing. Otherwise, we split
into two halves,
![$ \ensuremath{\mathtt{a0}}=\ensuremath{\mathtt{a[0]}},\ldots,\ensuremath{\mathtt{a[n/2-1]}}$](img1215.png){kind=small}
and
![$ \ensuremath{\mathtt{a1}}=\ensuremath{\mathtt{a[n/2]}},\ldots,\ensuremath{\mathtt{a[n-1]}}$](img1216.png){kind=small}
.
We recursively sort
and
, and then we merge (the now sorted)
and
to get our fully sorted array
:
<T> void mergeSort(T[] a, Comparator<T> c) {
if (a.length <= 1) return;
T[] a0 = Arrays.copyOfRange(a, 0, a.length/2);
T[] a1 = Arrays.copyOfRange(a, a.length/2, a.length);
mergeSort(a0, c);
mergeSort(a1, c);
merge(a0, a1, a, c);
}
An example is shown in Figure 11.1.
Compared to sorting, merging the two sorted arrays
and
fairly
easy. We add elements to
one at a time. If
or
is empty
we add the next element from the other (non-empty) array. Otherwise,
we take the minimum of the next element in
and the next element in
and add it to
:
<T> void merge(T[] a0, T[] a1, T[] a, Comparator<T> c) {
int i0 = 0, i1 = 0;
for (int i = 0; i < a.length; i++) {
if (i0 == a0.length)
a[i] = a1[i1++];
else if (i1 == a1.length)
a[i] = a0[i0++];
else if (compare(a0[i0], a1[i1]) < 0)
a[i] = a0[i0++];
else
a[i] = a1[i1++];
}
}
Notice that the
algorithm performs at most
comparisons before running out of elements in one of
or
.
To understand the running-time of merge-sort, it is easiest to think
of it in terms of its recursion tree. Suppose for now that
is a
power of 2, so that
, and
is an integer.
Refer to Figure 11.2. Merge-sort turns the problem of
sorting
elements into 2 problems, each of sorting
elements.
These two subproblem are then turned into 2 problems each, for a total
of 4 subproblems, each of size
. These 4 subproblems become 8
subproblems of size
, and so on. At the bottom of this process,
subproblems, each of size 2, are converted into
problems,
each of size
. For each subproblem of size
, the time
spent merging and copying data is
. Since there are 
subproblems of size
, the total time spent working on problems
of size , not counting recursive calls, is
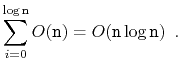
The proof of the following theorem is based on the same analysis as above,
but has to be a little more careful to deal with the cases where
is not a power of 2.
algorithm runs in
time and
performs at most
comparisons.
. The base case, in which
,
is trivial.
Merging two sorted lists of total length
requires at most
comparisons. Let
denote the maximum number of comparisons performed by
on an array
of length
. If
is even, then we apply the inductive hypothesis to
the two subproblems and obtain
 |
 |
|
 |
||
 |
||
 |
||
 |
is odd is slightly more complicated. For this case,
we use two inequalities, that are easy to verify:
and
. Inequality (![[*]](crossref.png)
) comes from the fact that
while () follows from the fact that 
is a concave function. With these tools in hand we have, for odd
,
|
 |
|
 |
||
 |
||
 |
||
 |
||
 |
||
 |
||
 |
The quicksort algorithm is another classic divide and conquer algorithm. Unlike merge-sort, which does merging after solving the two subproblems, quicksort does all its work upfront.
The algorithm is simple to describe: Pick a random pivot element,
, from
; partition
into the set of elements less than
, the
set of elements equal to
, and the set of elements greater than
;
and, finally, recursively sort the first and third sets in this partition.
An example is shown in Figure 11.3.
<T> void quickSort(T[] a, Comparator<T> c) {
quickSort(a, 0, a.length, c);
}
<T> void quickSort(T[] a, int i, int n, Comparator<T> c) {
if (n <= 1) return;
T x = a[i + rand.nextInt(n)];
int p = i-1, j = i, q = i+n;
// a[i..p]<x, a[p+1..q-1]??x, a[q..i+n-1]>x
while (j < q) {
int comp = compare(a[j], x);
if (comp < 0) { // move to beginning of array
swap(a, j++, ++p);
} else if (comp > 0) {
swap(a, j, --q); // move to end of array
} else {
j++; // keep in the middle
}
}
// a[i..p]<x, a[p+1..q-1]=x, a[q..i+n-1]>x
quickSort(a, i, p-i+1, c);
quickSort(a, q, n-(q-i), c);
}
All of this is done in-place, so that instead of making copies of
subarrays being sorted, the
method only sorts the
subarray
![$ \ensuremath{\mathtt{a[i]}},\ldots,\ensuremath{\mathtt{a[i+n-1]}}$](img1256.png){kind=small}
. Initially, this method is called
as
.
At the heart of the quicksort algorithm is the in-place partitioning that,
without any extra space, swaps elements in
and computes indices
and
so that
![$\displaystyle \ensuremath{\mathtt{a[i]}} \begin{cases}
{}< \ensuremath{\mathtt...
...htt{q}}\le \ensuremath{\mathtt{i}} \le \ensuremath{\mathtt{n}}-1$}
\end{cases}$](img1258.png)
loop in the code, works
by iteratively increasing
and decreasing
while maintaining the
first and last of these conditions. At each step, the element at position
is either moved to the front, left where it is, or moved to the back.
In the first two cases,
is incremented, while in the last case,
is not incremented since the new element at position
has not been
processed yet.
Quicksort is very closely related to the random binary search trees
studied in . In fact, if the input to quicksort consists
of
distinct elements, then the quicksort recursion tree is a random
binary search tree. To see this, recall that when constructing a random
binary search tree the first thing we do is pick a random element
and
make it the root of the tree. After this, every element will eventually
be compared to
, with smaller elements going into the left subtree
and larger elements going into the right subtree.
In quicksort, we select a random element
and immediately compare
everything to
, putting the smaller elements at the beginning of
the array and larger elements at the end of the array. Quicksort then
recursively sorts the beginning of the array and the end of the array,
while the random binary search tree recursively inserts smaller elements
in the left subtree of the root and larger elements in the right subtree
of the root.
The above correspondence between random binary search trees and quicksort means that we can translate Lemma 7.1 to a statement about quicksort:
, the expected number of times element
is compared to
a pivot element is at most
.A little summing of harmonic numbers gives us the following theorem about the running time of quicksort:
distinct elements,
the expected number of comparisons performed is
.
be the number of comparisons performed by quicksort when sorting
distinct elements. Using Lemma 11.1, we have:
![$\displaystyle \mathrm{E}[T]$](img554.png){kind=small} |
 |
|
 |
||
 |
||
 |
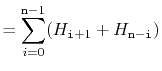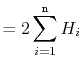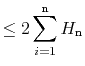Theorem 11.3 describes the case where the elements being sorted are
all distinct. When the input array,
, contains duplicate elements,
the expected running time of quicksort is no worse, and can be even
better; any time a duplicate element
is chosen as a pivot, all
occurrences of
get grouped together and don't take part in either
of the two subproblems.
method runs in
expected time
and the expected number of comparisons it performs is at most
.
The heap-sort algorithm is another in-place sorting algorithm.
Heap-sort uses the binary heaps discussed in .
Recall that the BinaryHeap data structure represents a heap using
a single array. The heap-sort algorithm converts the input array
into a heap and then repeatedly extracts the minimum value.
More specifically, a heap stores
elements at array locations
![$ \ensuremath{\mathtt{a[0]}},\ldots,\ensuremath{\mathtt{a[n-1]}}$](img1267.png){kind=small}
with the smallest value stored at the root,
![$ \mathtt{a[0]}$](img200.png){kind=small}
. After transforming
into a BinaryHeap, the heap-sort
algorithm repeatedly swaps
and
![$ \mathtt{a[n-1]}$](img201.png){kind=small}
, decrements
, and
calls
so that
![$ \ensuremath{\mathtt{a[0]}},\ldots,\ensuremath{\mathtt{a[n-2]}}$](img1269.png){kind=small}
once again are
a valid heap representation. When this process ends (because
)
the elements of
are stored in decreasing order, so
is reversed
to obtain the final sorted order.1Figure 11.1.3 shows an example of the execution of
.
|
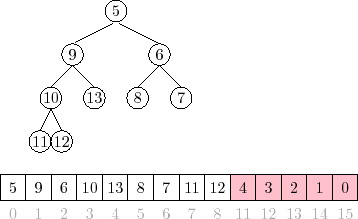
<T> void sort(T[] a, Comparator<T> c) {
BinaryHeap<T> h = new BinaryHeap<T>(a, c);
while (h.n > 1) {
h.swap(--h.n, 0);
h.trickleDown(0);
}
Collections.reverse(Arrays.asList(a));
}
A key subroutine in heap sort is the constructor for turning
an unsorted array
into a heap. It would be easy to do this
in
time by repeatedly calling the BinaryHeap
method, but we can do better by using a bottom-up algorithm.
Recall that, in a binary heap, the children of
![$ \mathtt{a[i]}$](img199.png){kind=small}
are stored at
positions
![$ \mathtt{a[2i+1]}$](img1274.png){kind=small}
and
![$ \mathtt{a[2i+2]}$](img1275.png){kind=small}
. This implies that the elements
![$ \ensuremath{\mathtt{a}}[\lfloor\ensuremath{\mathtt{n}}/2\rfloor],\ldots,\ensuremath{\mathtt{a[n-1]}}$](img1276.png){kind=small}
have no children. In other
words, each of
is a sub-heap
of size 1. Now, working backwards, we can call
for
each
. This works, because by
the time we call
, each of the two children of
are the root of a sub-heap so calling
makes
into the root of its own subheap.
BinaryHeap(T[] a, Comparator<T> c) {
this.c = c;
this.a = a;
n = a.length;
for (int i = n/2-1; i >= 0; i--) {
trickleDown(i);
}
}
The interesting thing about this bottom-up strategy is that it is more
efficient than calling
times. To see this, notice that,
for
elements, we do no work at all, for
elements, we call
on a subheap rooted at
and whose height is 1, for
elements, we call
on a subheap whose height is 2,
and so on. Since the work done by
is proportional to
the height of the sub-heap rooted at
, this means that the total
work done is at most
is equal, by definition, to the expected
number times we toss a coin up to and including the first time the coin
comes up as heads and applying Lemma 4.2.
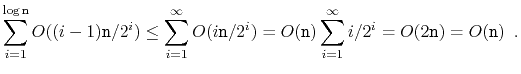
The following theorem describes the performance of
.
method runs in
time and performs at
most
comparisons.
into a heap,
(2) repeatedly extracting the minimum element from
, and (3) reversing
the elements in
. We have just argued that step 1 takes
time and performs
comparisons. Step 3 takes
time and
performs no comparisons. Step 2 performs
calls to
.
The 
th such call operates on a heap of size
and performs
at most
comparisons. Summing this over gives
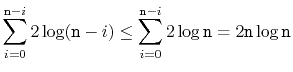
We have now seen three comparison-based sorting algorithms that each run
in
time. By now, we should be wondering if faster
algorithms exist. The short answer to this question is no. If the
only operations allowed on the elements of
are comparisons then no
algorithm can avoid doing roughly
comparisons. This is
not difficult to prove, but requires a little imagination. Ultimately,
it follows from the fact that
We will first focus our attention on deterministic algorithms like
merge-sort and heap-sort and on a particular fixed value of
. Imagine
such an algorithm is being used to sort
distinct elements. The key
to proving the lower-bound is to observe that, for a deterministic
algorithm with a fixed value of
, the first pair of elements that are
compared is always the same. For example, in
, when
is even, the first call to
is with
and the
first comparison is between elements
![$ \mathtt{a[n/2-1]}$](img1287.png){kind=small}
and
.
Since all input elements are distinct, this first comparison has only
two possible outcomes. The second comparison done by the algorithm may
depend on the outcome of the first comparison. The third comparison
may depend on the results of the first two, and so on. In this way,
any deterministic comparison-based sorting algorithm can be viewed
as a rooted binary comparison-tree. Each internal node,
,
of this tree is labelled with a pair of of indices
and
.
If
![$ \ensuremath{\mathtt{a[u.i]}}<\ensuremath{\mathtt{a[u.j]}}$](img1290.png){kind=small}
the algorithm proceeds to the left subtree,
otherwise it proceeds to the right subtree. Each leaf
of this
tree is labelled with a permutation
![$ \ensuremath{\mathtt{w.p[0]}},\ldots,\ensuremath{\mathtt{w.p[n-1]}}$](img1291.png){kind=small}
of
. This permutation represents the permutation that is
required to sort
if the comparison tree reaches this leaf. That is,
![$\displaystyle \ensuremath{\mathtt{a[w.p[0]]}}<\ensuremath{\mathtt{a[w.p[1]]}}<\cdots<\ensuremath{\mathtt{a[w.p[n-1]]}} \enspace .
$](img1292.png){kind=small}
is shown in
Figure 11.5.
The comparison tree for a sorting algorithm tells us everything about
the algorithm. It tells us exactly the sequence of comparisons that will
be performed for any input array
having
distinct elements and
it tells us how the algorithm will reorder
to sort it.
An immediate consequence of this is that the comparison tree must have
at least
leaves; if not, then there are two distinct permutations
that lead to the same leaf, so the algorithm does not correctly sort at
least one of these permutations.
For example, the comparison tree in Figure 11.6 has only
leaves. Inspecting this tree, we see that the two input arrays
and 
both lead to the rightmost leaf. On the input
this leaf correctly outputs
![$ \ensuremath{\mathtt{a[1]}}=1,\ensuremath{\mathtt{a[2]}}=2,\ensuremath{\mathtt{a[0]}}=3$](img1299.png){kind=small}
. However, on the
input , this node incorrectly outputs
![$ \ensuremath{\mathtt{a[1]}}=2,\ensuremath{\mathtt{a[2]}}=1,\ensuremath{\mathtt{a[0]}}=3$](img1300.png){kind=small}
.
This discussion leads to the primary lower-bound for comparison-based
algorithms.
and any integer
, there exists an input array
of
length
such that
performs at least
comparisons when sorting
.
must have at least
leaves. An easy inductive proof shows
that any binary tree with 
leaves has height at least 
.
Therefore, the comparison tree for
has a leaf,
, of
depth at least
and there is an input array
that leads
to this leaf. The input array
is an input for which
does at least
comparisons.
Theorem 11.5 deals with deterministic
algorithms like merge-sort and heap-sort, but doesn't tell us anything
about randomized algorithms like quicksort. Could a randomized algorithm
beat the
lower bound on the number of comparisons?
The answer, again, is no. Again, the way to prove it is to think
differently about what a randomized algorithm is.
In the following discussion, we will implicitly assume that our decision
trees have been ``cleaned up'' in the following way: Any node that can not
be reached by some input array
is removed. This cleaning up implies
that the tree has exactly
leaves. It has at least
leaves
because, otherwise, it could not sort correctly. It has at most
leaves since each of the possible
permutation of
distinct
elements follows exactly one root to leaf path in the decision tree.
We can think of a randomized sorting algorithm
as a
deterministic algorithm that takes two inputs: The input array
that should be sorted and a long sequence
of
random real numbers in the range ![$ [0,1]$](img1307.png){kind=small}
. The random numbers provide
the randomization. When the algorithm wants to toss a coin or make a
random choice, it does so by using some element from 
. For example,
to compute the index of the first pivot in quicksort, the algorithm
could use the formula
.
Now, notice that if we fix to some particular sequence 
then
becomes a deterministic sorting algorithm,
, that has an associated comparison tree,
. Next, notice that if we select
to be a random
permutation of
, then this is equivalent to selecting
a random leaf,
, from the
leaves of
.
Exercise 11.6 asks you to prove that, if we select
a random leaf from any binary tree with leaves, then the expected
depth of that leaf is at least . Therefore, the expected
number of comparisons performed by the (deterministic) algorithm
when given an input array containing a random
permutation of
is at least
. Finally,
notice that this is true for every choice of , therefore it holds even for
. This completes the proof of the lower-bound for randomized algorithms.
and any integer
, the expected number of comparisons done by
when sorting a random permutation of
is
at least
.
function so that the
heap sort algorithm stores the elements directly in ascending order.
![$ \ensuremath{\mathtt{a[0]}},\ensuremath{\mathtt{a[1]}},\ensuremath{\mathtt{a[2]}}$](img1295.png){kind=small}
