Next: 12.3 Graph Traversal Up: 12. Graphs Previous: 12.1 AdjacencyMatrix: Representing a Contents Index
Adjacency list representations of graphs take a more vertex-centric
approach. There are many possible implementations of adjacency lists.
In this section, we present a simple one. At the end of the section,
we discuss different possibilities. In an adjacency list representation,
the graph ![]() is represented as an array,
is represented as an array,
![]() , of lists. The list
, of lists. The list
![]() contains a list of all the vertices adjacent to vertex
contains a list of all the vertices adjacent to vertex
![]() .
That is, it contains every index
.
That is, it contains every index
![]() such that
such that
![]() .
.

(An example is shown in Figure 12.3.) In this particular
implementation, we represent each list in
![]() as ArrayStack, because we would like constant time access
by position. Other options are also possible. Specifically, we could
have implemented
as ArrayStack, because we would like constant time access
by position. Other options are also possible. Specifically, we could
have implemented
![]() as a DLList.
as a DLList.
![\includegraphics[scale=0.90909]{figs-python/graph}](img4626.png)
|
The
![]() operation just appends the value
operation just appends the value
![]() to the list
to the list
![]() :
:
![\begin{leftbar}
\begin{flushleft}
\hspace*{1em} \ensuremath{\mathrm{add\_edge}(\...
...t{i}}].\mathrm{append}(\ensuremath{\mathit{j}})}\\
\end{flushleft}\end{leftbar}](img4630.png)
This takes constant time.
The
![]() operation searches through the list
operation searches through the list
![]() until it finds
until it finds
![]() and then removes it:
and then removes it:

This takes
![]() time, where
time, where
![]() (the degree
of
(the degree
of
![]() ) counts the number of edges in
) counts the number of edges in ![]() that have
that have
![]() as their source.
as their source.
The
![]() operation is similar; it searches through the list
operation is similar; it searches through the list
![]() until it finds
until it finds
![]() (and returns true), or reaches the end of
the list (and returns false):
(and returns true), or reaches the end of
the list (and returns false):
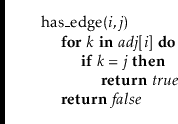
This also takes
![]() time.
time.
The
![]() operation is very simple;
it returns the list
operation is very simple;
it returns the list
![]() :
:
![\begin{leftbar}
\begin{flushleft}
\hspace*{1em} \ensuremath{\mathrm{out\_edges}(...
...suremath{\mathit{adj}}[\ensuremath{\mathit{i}}]}\\
\end{flushleft}\end{leftbar}](img4647.png)
The
![]() operation is much more work. It scans over every
vertex
operation is much more work. It scans over every
vertex ![]() checking if the edge
checking if the edge
![]() exists and, if so, adding
exists and, if so, adding
![]() to the output list:
to the output list:

This operation is very slow. It scans the adjacency list of every vertex,
so it takes
![]() time.
time.
The following theorem summarizes the performance of the above data structure:
As alluded to earlier, there are many different choices to be made when implementing a graph as an adjacency list. Some questions that come up include:
opendatastructures.org