Next: 8.2 Discussion and Exercises Up: 8. Scapegoat Trees Previous: 8. Scapegoat Trees Contents Index
A
![]() is a
is a
![]() that, in addition to keeping
track of the number,
that, in addition to keeping
track of the number,
![]() , of nodes in the tree also keeps a counter,
, of nodes in the tree also keeps a counter,
![]() ,
that maintains an upper-bound on the number of nodes.
,
that maintains an upper-bound on the number of nodes.
int q;At all times,
Implementing the
![]() operation in a
operation in a
![]() is done
using the standard algorithm for searching in a
is done
using the standard algorithm for searching in a
![]() (see Section 6.2). This takes time proportional to the
height of the tree which, by (8.1) is
(see Section 6.2). This takes time proportional to the
height of the tree which, by (8.1) is
![]() .
.
To implement the
![]() operation, we first increment
operation, we first increment
![]() and
and
![]() and then use the usual algorithm for adding
and then use the usual algorithm for adding
![]() to a binary search
tree; we search for
to a binary search
tree; we search for
![]() and then add a new leaf
and then add a new leaf
![]() with
with
![]() .
At this point, we may get lucky and the depth of
.
At this point, we may get lucky and the depth of
![]() might not exceed
might not exceed
![]() . If so, then we leave well enough alone and don't do
anything else.
. If so, then we leave well enough alone and don't do
anything else.
Unfortunately, it will sometimes happen that
![]() . In this case, we need to reduce the height. This isn't a big
job; there is only one node, namely
. In this case, we need to reduce the height. This isn't a big
job; there is only one node, namely
![]() , whose depth exceeds
, whose depth exceeds
![]() . To fix
. To fix
![]() , we walk from
, we walk from
![]() back up to the root looking for a
scapegoat,
back up to the root looking for a
scapegoat,
![]() . The scapegoat,
. The scapegoat,
![]() , is a very unbalanced node.
It has the property that
, is a very unbalanced node.
It has the property that
bool add(T x) {
// first do basic insertion keeping track of depth
Node *u = new Node;
u->x = x;
u->left = u->right = u->parent = nil;
int d = addWithDepth(u);
if (d > log32(q)) {
// depth exceeded, find scapegoat
Node *w = u->parent;
int a = BinaryTree<Node>::size(w);
int b = BinaryTree<Node>::size(w->parent);
while (3*a <= 2*b) {
w = w->parent;
a = BinaryTree<Node>::size(w);
b = BinaryTree<Node>::size(w->parent);
}
rebuild(w->parent);
}
return d >= 0;
}
|
The implementation of
![]() in a
in a
![]() is very simple.
We search for
is very simple.
We search for
![]() and remove it using the usual algorithm for removing a
node from a
and remove it using the usual algorithm for removing a
node from a
![]() . (Note that this can never increase the
height of the tree.) Next, we decrement
. (Note that this can never increase the
height of the tree.) Next, we decrement
![]() , but leave
, but leave
![]() unchanged.
Finally, we check if
unchanged.
Finally, we check if
![]() and, if so, then we rebuild the entire
tree into a perfectly balanced binary search tree and set
and, if so, then we rebuild the entire
tree into a perfectly balanced binary search tree and set
![]() .
.
bool remove(T x) {
if (BinarySearchTree<Node,T>::remove(x)) {
if (2*n < q) {
rebuild(r);
q = n;
}
return true;
}
return false;
}
Again, if we ignore the cost of rebuilding, the running time of the
In this section, we analyze the correctness and amortized running time
of operations on a
![]() . We first prove the correctness by
showing that, when the
. We first prove the correctness by
showing that, when the
![]() operation results in a node that violates
Condition (8.1), then we can always find a scapegoat:
operation results in a node that violates
Condition (8.1), then we can always find a scapegoat:
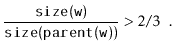
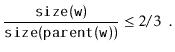
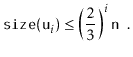
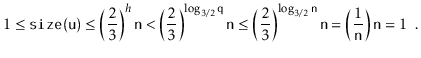
Next, we analyze the parts of the running time that are not yet
accounted for. There are two parts: The cost of calls to
![]() when searching for scapegoat nodes, and the cost of calls to
when searching for scapegoat nodes, and the cost of calls to
![]() when we find a scapegoat
when we find a scapegoat
![]() . The cost of calls to
. The cost of calls to
![]() can be
related to the cost of calls to
can be
related to the cost of calls to
![]() , as follows:
, as follows:
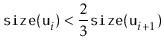
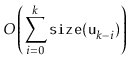 |
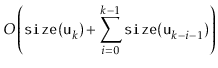 |
||
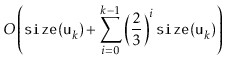 |
|||
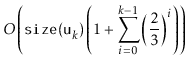 |
|||
All that remains is to prove an upper-bound on the cost of all calls to
![]() during a sequence of
during a sequence of ![]() operations:
operations:
During an insertion or deletion, we give one credit to each node on the
path to the inserted node, or deleted node,
![]() . In this way we hand
out at most
. In this way we hand
out at most
![]() credits per operation.
During a deletion we also store an additional credit ``on the side.''
Thus, in total we give out at most
credits per operation.
During a deletion we also store an additional credit ``on the side.''
Thus, in total we give out at most
![]() credits. All that
remains is to show that these credits are sufficient to pay for all
calls to
credits. All that
remains is to show that these credits are sufficient to pay for all
calls to
![]() .
.
If we call
![]() during an insertion, it is because
during an insertion, it is because
![]() is
a scapegoat. Suppose, without loss of generality, that
is
a scapegoat. Suppose, without loss of generality, that
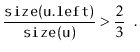
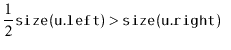
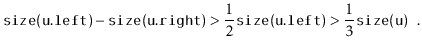
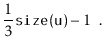
If we call
![]() during a deletion, it is because
during a deletion, it is because
![]() .
In this case, we have
.
In this case, we have
![]() credits stored ``on the side,'' and
we use these to pay for the
credits stored ``on the side,'' and
we use these to pay for the
![]() time it takes to rebuild the root.
This completes the proof.
time it takes to rebuild the root.
This completes the proof.
![]()
Furthermore, beginning with an empty
![]() , any sequence of
, any sequence of ![]()
![]() and
and
![]() operations results in a total of
operations results in a total of
![]() time spent during all calls to
time spent during all calls to
![]() .
.
opendatastructures.org