Next: 13.4 Discussion and Exercises Up: 13. Data Structures for Previous: 13.2 : Searching in Contents Index
The
![]() is a vast--even exponential--improvement over the
is a vast--even exponential--improvement over the
![]() in terms of query time, but the
in terms of query time, but the
![]() and
and
![]() operations are still not terribly fast. Furthermore, the space usage,
operations are still not terribly fast. Furthermore, the space usage,
![]() , is higher than the other
, is higher than the other
![]() implementations
described in this book, which all use
implementations
described in this book, which all use
![]() space. These two
problems are related; if
space. These two
problems are related; if
![]()
![]() operations build a structure of
size
operations build a structure of
size
![]() , then the
, then the
![]() operation requires at least on the
order of
operation requires at least on the
order of
![]() time (and space) per operation.
time (and space) per operation.
The
![]() , discussed next, simultaneously improves the space and
speed of
, discussed next, simultaneously improves the space and
speed of
![]() s. A
s. A
![]() uses an
uses an
![]() ,
,
![]() , but only
stores
, but only
stores
![]() values in
values in
![]() . In this way, the total space used by
. In this way, the total space used by
![]() is only
is only
![]() . Furthermore, only one out of every
. Furthermore, only one out of every
![]()
![]() or
or
![]() operations in the
operations in the
![]() results in an
results in an
![]() or
or
![]() operation in
operation in
![]() . By doing this, the average cost incurred
by calls to
. By doing this, the average cost incurred
by calls to
![]() 's
's
![]() and
and
![]() operations is only constant.
operations is only constant.
The obvious question becomes: If
![]() only stores
only stores
![]() /
/
![]() elements,
where do the remaining
elements,
where do the remaining
![]() elements go? These elements move
into secondary structures,
in this case an extended version of
treaps (Section 7.2). There are roughly
elements go? These elements move
into secondary structures,
in this case an extended version of
treaps (Section 7.2). There are roughly
![]() /
/
![]() of these secondary
structures so, on average, each of them stores
of these secondary
structures so, on average, each of them stores
![]() items. Treaps
support logarithmic time
items. Treaps
support logarithmic time
![]() operations, so the operations on these
treaps will run in
operations, so the operations on these
treaps will run in
![]() time, as required.
time, as required.
More concretely, a
![]() contains an
contains an
![]() ,
,
![]() ,
that contains a random sample of the data, where each element
appears in the sample independently with probability
,
that contains a random sample of the data, where each element
appears in the sample independently with probability
![]() .
For convenience, the value
.
For convenience, the value
![]() , is always contained in
, is always contained in
![]() .
Let
.
Let
![]() denote the elements stored in
denote the elements stored in
![]() .
Associated with each element,
.
Associated with each element,
![]() , is a treap,
, is a treap,
![]() , that stores
all values in the range
, that stores
all values in the range
![]() . This is illustrated
in Figure 13.7.
. This is illustrated
in Figure 13.7.
The
![]() operation in a
operation in a
![]() is fairly easy. We search
for
is fairly easy. We search
for
![]() in
in
![]() and find some value
and find some value
![]() associated with the treap
associated with the treap
![]() . We then use the treap
. We then use the treap
![]() method on
method on
![]() to answer
the query. The entire method is a one-liner:
to answer
the query. The entire method is a one-liner:
T find(T x) {
return xft.find(YPair<T>(intValue(x))).t->find(x);
}
The first
Adding an element to a
![]() is also fairly simple--most of
the time. The
is also fairly simple--most of
the time. The
![]() method calls
method calls
![]() to locate the treap,
to locate the treap,
![]() , into which
, into which
![]() should be inserted. It then calls
should be inserted. It then calls
![]() to
add
to
add
![]() to
to
![]() . At this point, it tosses a biased coin that comes up as
heads with probability
. At this point, it tosses a biased coin that comes up as
heads with probability
![]() and as tails with probability
and as tails with probability
![]() .
If this coin comes up heads, then
.
If this coin comes up heads, then
![]() will be added to
will be added to
![]() .
.
This is where things get a little more complicated. When
![]() is added to
is added to
![]() , the treap
, the treap
![]() needs to be split into two treaps,
needs to be split into two treaps,
![]() and
and
![]() .
The treap
.
The treap
![]() contains all the values less than or equal to
contains all the values less than or equal to
![]() ;
;
![]() is the original treap,
is the original treap,
![]() , with the elements of
, with the elements of
![]() removed.
Once this is done, we add the pair
removed.
Once this is done, we add the pair
![]() to
to
![]() . Figure 13.8
shows an example.
. Figure 13.8
shows an example.
bool add(T x) {
unsigned ix = intValue(x);
Treap1<T> *t = xft.find(YPair<T>(ix)).t;
if (t->add(x)) {
n++;
if (rand() % w == 0) {
Treap1<T> *t1 = (Treap1<T>*)t->split(x);
xft.add(YPair<T>(ix, t1));
}
return true;
}
return false;
return true;
}
![\includegraphics[scale=0.90909]{figs/yfast-add}](img6017.png)
|
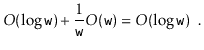
The
![]() method undoes the work performed by
method undoes the work performed by
![]() .
We use
.
We use
![]() to find the leaf,
to find the leaf,
![]() , in
, in
![]() that contains the answer
to
that contains the answer
to
![]() . From
. From
![]() , we get the treap,
, we get the treap,
![]() , containing
, containing
![]() and remove
and remove
![]() from
from
![]() . If
. If
![]() was also stored in
was also stored in
![]() (and
(and
![]() is not equal to
is not equal to
![]() ) then we remove
) then we remove
![]() from
from
![]() and add the
elements from
and add the
elements from
![]() 's treap to the treap,
's treap to the treap,
![]() , that is stored by
, that is stored by
![]() 's
successor in the linked list. This is illustrated in
Figure 13.9.
's
successor in the linked list. This is illustrated in
Figure 13.9.
bool remove(T x) {
unsigned ix = intValue(x);
XFastTrieNode1<YPair<T> > *u = xft.findNode(ix);
bool ret = u->x.t->remove(x);
if (ret) n--;
if (u->x.ix == ix && ix != UINT_MAX) {
Treap1<T> *t2 = u->child[1]->x.t;
t2->absorb(*u->x.t);
xft.remove(u->x);
}
return ret;
}
Finding the node
Earlier in the discussion, we delayed arguing about the sizes of treaps in this structure until later. Before finishing this chapter, we prove the result we need.
Similarly, the elements of
![]() smaller than
smaller than
![]() are
are
![]() where all these
where all these ![]() coin tosses turn up as
tails and the coin toss for
coin tosses turn up as
tails and the coin toss for
![]() turns up as heads. Therefore,
turns up as heads. Therefore,
![]() , since this is the same coin tossing experiment considered
in the preceding paragraph, but one in which the last toss is not counted.
In summary,
, since this is the same coin tossing experiment considered
in the preceding paragraph, but one in which the last toss is not counted.
In summary,
![]() , so
, so
![\includegraphics[width=\textwidth ]{figs/yfast-sample}](img6103.png)
|
Lemma 13.1 was the last piece in the proof of the
following theorem, which summarizes the performance of the
![]() :
:
The
![]() term in the space requirement comes from the fact that
term in the space requirement comes from the fact that
![]() always
stores the value
always
stores the value
![]() . The implementation could be modified (at the
expense of adding some extra cases to the code) so that it is unnecessary
to store this value. In this case, the space requirement in the theorem
becomes
. The implementation could be modified (at the
expense of adding some extra cases to the code) so that it is unnecessary
to store this value. In this case, the space requirement in the theorem
becomes
![]() .
.