The
 ,
,
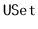 , and
, and
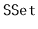 interfaces described in
Section 1.2 are influenced by the Java Collections Framework
[54].
These are essentially simplified versions of
the
interfaces described in
Section 1.2 are influenced by the Java Collections Framework
[54].
These are essentially simplified versions of
the
 ,
,
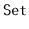 ,
,
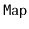 ,
,
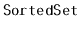 , and
, and
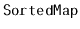 interfaces found in
the Java Collections Framework.
interfaces found in
the Java Collections Framework.
For a superb (and free) treatment of the mathematics discussed in this
chapter, including asymptotic notation, logarithms, factorials, Stirling's
approximation, basic probability, and lots more, see the textbook by
Leyman, Leighton, and Meyer [50]. For a gentle calculus text
that includes formal definitions of exponentials and logarithms, see the
(freely available) classic text by Thompson [71].
For more information on basic probability, especially as it relates to
computer science, see the textbook by Ross [63]. Another good
reference, which covers both asymptotic notation and probability, is
the textbook by Graham, Knuth, and Patashnik [37].
Exercise 1..1
This exercise is designed to help familiarize the reader with choosing
the right data structure for the right problem. If implemented, the
parts of this exercise should be done by making use of an implementation
of the relevant interface (
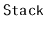
,
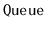
,
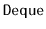
,
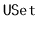
, or
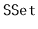
)
provided by the C++
Standard Template Library.
Solve the following problems by reading a text file one line at a
time and performing operations on each line in the appropriate data
structure(s). Your implementations should be fast enough that even
files containing a million lines can be processed in a few seconds.
- Read the input one line at a time and then write the lines out
in reverse order, so that the last input line is printed first,
then the second last input line, and so on.
- Read the first 50 lines of input and then write them out in
reverse order. Read the next 50 lines and then write them out in
reverse order. Do this until there are no more lines left to read,
at which point any remaining lines should be output in reverse
order.
In other words, your output will start with the 50th line, then
the 49th, then the 48th, and so on down to the first line. This
will be followed by the 100th line, followed by the 99th, and so
on down to the 51st line. And so on.
Your code should never have to store more than 50 lines at any
given time.
- Read the input one line at a time.
At any point after reading the first 42 lines, if some line is blank
(i.e., a string of length 0), then output the line that occured
42 lines prior to that one. For example, if Line 242 is blank,
then your program should output line 200. This program should
be implemented so that it never stores more than 43 lines of the
input at any given time.
- Read the input one line at a time and write each line to the
output if it is not a duplicate of some previous input line. Take
special care so that a file with a lot of duplicate lines does not
use more memory than what is required for the number of unique lines.
- Read the input one line at a time and write each line to the
output only if you have already read this line before. (The end
result is that you remove the first occurrence of each line.)
Take special care so that a file with a lot of duplicate lines
does not use more memory than what is required for the number of
unique lines.
- Read the entire input one line at a time. Then output all lines
sorted by length, with the shortest lines first. In the case where
two lines have the same length, resolve their order using the usual
``sorted order.'' Duplicate lines should be printed only once.
- Do the same as the previous question except that duplicate lines
should be printed the same number of times that they appear in the input.
- Read the entire input one line at a time and then output the
even numbered lines (starting with the first line, line 0) followed
by the odd-numbered lines.
- Read the entire input one line at a time and randomly permute
the lines before outputting them. To be clear: You should not
modify the contents of any line. Instead, the same collection of
lines should be printed, but in a random order.
Exercise 1..2
A
Dyck word is a sequence of +1's and -1's with the property that
the sum of any prefix of the sequence is never negative. For example,
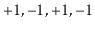
is a Dyck word, but
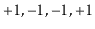
is not a Dyck word
since the prefix
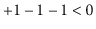
. Describe any relationship
between Dyck words and
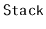
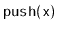
and
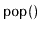
operations.
Exercise 1..3
A
matched string is a sequence of {, }, (, ), [, and ]
characters that are properly matched. For example, ``{{()[]}}''
is a matched string, but this ``{{()]}'' is not, since the second {
is matched with a ]. Show how to use a stack so that, given a string
of length
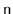
, you can determine if it is a matched string in
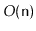
time.
Exercise 1..4
Suppose you have a
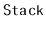
,
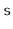
, that supports only the
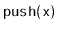
and
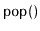
operations. Show how, using only a FIFO
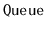
,
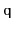
,
you can reverse the order of all elements in
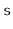
.
Exercise 1..5
Using a
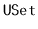
, implement a
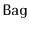
. A
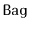
is like a
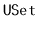
--it
supports the
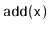
,
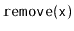
and
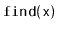
methods--but it allows
duplicate elements to be stored. The
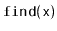
operation in a
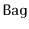
returns some element (if any) that is equal to
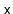
. In addition,
a
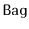
supports the
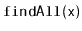
operation that returns a list of
all elements in the
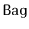
that are equal to
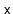
.
Exercise 1..6
From scratch, write and test implementations of the

,
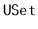
and
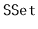
interfaces. These do not have to be efficient. They can
be used later to test the correctness and performance of more efficient
implementations. (The easiest way to do this is to store the elements
in an array.)
Exercise 1..7
Work to improve the performance of your implementations from the
previous question using any tricks you can think of. Experiment and
think about how you could improve the performance of
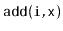
and
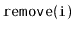
in your

implementation. Think about how you could
improve the performance of the
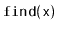
operation in your
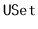
and
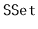
implementations. This exercise is designed to give you a
feel for how difficult it can be to obtain efficient implementations
of these interfaces.
opendatastructures.org
![]() ,
,
![]() , and
, and
![]() interfaces described in
Section 1.2 are influenced by the Java Collections Framework
[54].
These are essentially simplified versions of
the
interfaces described in
Section 1.2 are influenced by the Java Collections Framework
[54].
These are essentially simplified versions of
the
![]() ,
,
![]() ,
,
![]() ,
,
![]() , and
, and
![]() interfaces found in
the Java Collections Framework.
interfaces found in
the Java Collections Framework.