4.5 Discussion and Exercises

Skiplists were introduced by Pugh [60] who also presented a number of applications and extensions of skiplists [59]. Since then they have been studied extensively. Several researchers have done very precise analyses of the expected length and variance of the length of the search path for the 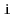$\mathtt{i}$th element in a skiplist [45,44,56]. Deterministic versions [53], biased versions [8,26], and self-adjusting versions [12] of skiplists have all been developed. Skiplist implementations have been written for various languages and frameworks and have been used in open-source database systems [69,61]. A variant of skiplists is used in the HP-UX operating system kernel's process management structures [42].

Exercise 4..1   Illustrate the search paths for 2.5 and 5.5 on the skiplist in Figure 4.1.

Exercise 4..2   Illustrate the addition of the values 0.5 (with a height of 1) and then 3.5 (with a height of 2) to the skiplist in Figure 4.1.

Exercise 4..3   Illustrate the removal of the values 1 and then 3 from the skiplist in Figure 4.1.

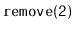
Exercise 4..4   Illustrate the execution of $\mathtt{remove(2)}$ on the $\mathtt{SkiplistList}$ in Figure 4.5.

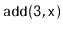
Exercise 4..5   Illustrate the execution of $\mathtt{add(3,x)}$ on the $\mathtt{SkiplistList}$ in Figure 4.5. Assume that $\mathtt{pickHeight()}$ selects a height of 4 for the newly created node.

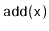
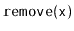
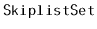
Exercise 4..6   Show that, during an $\mathtt{add(x)}$ or a $\mathtt{remove(x)}$ operation, the expected number of pointers in a $\mathtt{SkiplistSet}$ that get changed is constant.

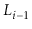
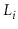
Exercise 4..7   Suppose that, instead of promoting an element from $L_{i-1}$ into $L_i$ based on a coin toss, we promote it with some probability $p$, $0 < p < 1$.

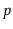
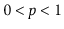
1. Show that, with this modification, the expected length of a search path is at most $(1/p)\log_{1/p} \ensuremath{\mathtt{n}} + O(1)$.
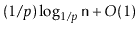2. What is the value of 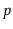$p$ that minimizes the preceding expression?
3. What is the expected height of the skiplist?
4. What is the expected number of nodes in the skiplist?

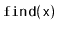
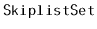
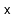
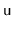
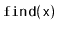
Exercise 4..8   The $\mathtt{find(x)}$ method in a $\mathtt{SkiplistSet}$ sometimes performs redundant comparisons; these occur when $\mathtt{x}$ is compared to the same value more than once. They can occur when, for some node, $\mathtt{u}$, $\ensuremath{\mathtt{u.next[r]}} = \ensuremath{\mathtt{u.next[r-1]}}$. Show how these redundant comparisons happen and modify $\mathtt{find(x)}$ so that they are avoided. 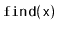Analyze the expected number of comparisons done by your modified $\mathtt{find(x)}$ method.

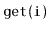
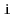
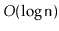
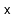
Exercise 4..9   Design and implement a version of a skiplist that implements the $\mathtt{SSet}$ interface, but also allows fast access to elements by rank. That is, it also supports the function $\mathtt{get(i)}$, which returns the element whose rank is $\mathtt{i}$ in $O(\log \ensuremath{\mathtt{n}})$ expected time. 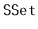(The rank of an element $\mathtt{x}$ in an $\mathtt{SSet}$ is the number of elements in the $\mathtt{SSet}$ that are less than $\mathtt{x}$.)

Exercise 4..10   A finger in a skiplist is an array that stores the sequence of nodes on a search path at which the search path goes down. (The variable $\mathtt{stack}$ in the $\mathtt{add(x)}$ code on page  is a finger; the shaded nodes in Figure 4.3 show the contents of the finger.) One can think of a finger as pointing out the path to a node in the lowest list, $L_0$.

A finger search implements the $\mathtt{find(x)}$ operation using a finger, by walking up the list using the finger until reaching a node $\mathtt{u}$ such that $\ensuremath{\mathtt{u.x}} < \ensuremath{\mathtt{x}}$ and $\ensuremath{\mathtt{u.next}}=\ensuremath{\mathtt{null}}$ or $\ensuremath{\mathtt{u.next.x}} > \ensuremath{\mathtt{x}}$ and then performing a normal search for $\mathtt{x}$ starting from $\mathtt{u}$. It is possible to prove that the expected number of steps required for a finger search is $O(1+\log r)$, where $r$ is the number values in $L_0$ between $\mathtt{x}$ and the value pointed to by the finger.

Implement a subclass of $\mathtt{Skiplist}$ called $\mathtt{SkiplistWithFinger}$ that implements $\mathtt{find(x)}$ operations using an internal finger. This subclass stores a finger, which is then used so that every $\mathtt{find(x)}$ operation is implemented as a finger search. During each $\mathtt{find(x)}$ operation the finger is updated so that each $\mathtt{find(x)}$ operation uses, as a starting point, a finger that points to the result of the previous $\mathtt{find(x)}$ operation.

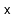
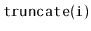
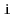
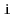
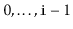
Exercise 4..11   Write a method, $\mathtt{truncate(i)}$, that truncates a $\mathtt{SkiplistList}$ at position $\mathtt{i}$. After the execution of this method, the size of the list is $\mathtt{i}$ and it contains only the elements at indices $0,\ldots,\ensuremath{\mathtt{i}}-1$. The return value is another $\mathtt{SkiplistList}$ that contains the elements at indices $\ensuremath{\mathtt{i}},\ldots,\ensuremath{\mathtt{n}}-1$. 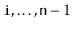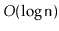This method should run in $O(\log \ensuremath{\mathtt{n}})$ time.

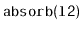
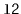
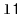
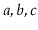
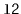
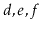
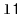
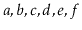
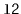
Exercise 4..12   Write a $\mathtt{SkiplistList}$ method, $\mathtt{absorb(l2)}$, that takes as an argument a $\mathtt{SkiplistList}$, $\mathtt{l2}$, empties it and appends its contents, in order, to the receiver. For example, if $\mathtt{l1}$ contains $a,b,c$ and $\mathtt{l2}$ contains $d,e,f$, then after calling $\mathtt{l1.absorb(l2)}$, $\mathtt{l1}$ will contain $a,b,c,d,e,f$ and $\mathtt{l2}$ will be empty. 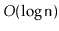This method should run in $O(\log \ensuremath{\mathtt{n}})$ time.

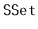
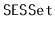
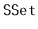
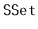
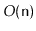
Exercise 4..13   Using the ideas from the space-efficient list, $\mathtt{SEList}$, design and implement a space-efficient $\mathtt{SSet}$, $\mathtt{SESSet}$. To do this, store the data, in order, in an $\mathtt{SEList}$, and store the blocks of this $\mathtt{SEList}$ in an $\mathtt{SSet}$. 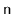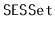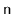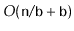If the original $\mathtt{SSet}$ implementation uses $O(\ensuremath{\mathtt{n}})$ space to store $\mathtt{n}$ elements, then the $\mathtt{SESSet}$ will use enough space for $\mathtt{n}$ elements plus $O(\ensuremath{\mathtt{n}}/\ensuremath{\mathtt{b}}+\ensuremath{\mathtt{b}})$ wasted space.

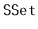
Exercise 4..14   Using an $\mathtt{SSet}$ as your underlying structure, design and implement an application that reads a (large) text file and allows you to search, interactively, for any substring contained in the text. As the user types their query, a matching part of the text (if any) should appear as a result.

Hint 1: Every substring is a prefix of some suffix, so it suffices to store all suffixes of the text file.

Hint 2: Any suffix can be represented compactly as a single integer indicating where the suffix begins in the text.

Test your application on some large texts, such as some of the books available at Project Gutenberg [1]. If done correctly, your applications will be very responsive; there should be no noticeable lag between typing keystrokes and seeing the results.

Exercise 4..15   (This excercise should be done after reading about binary search trees, in Section 6.2.) Compare skiplists with binary search trees in the following ways:

1. Explain how removing some edges of a skiplist leads to a structure that looks like a binary tree and is similar to a binary search tree.
2. Skiplists and binary search trees each use about the same number of pointers (2 per node). Skiplists make better use of those pointers, though. Explain why.