Most of the data structures described in this chapter are folklore. They
can be found in implementations dating back over 30 years. For example,
implementations of stacks, queues, and deques which generalize easily
to the ArrayStack, ArrayQueue and ArrayDeque structures described
here are discussed by Knuth [46, Section 2.2.2].
Brodnik et al. [13] seem to have been the first to describe
the RootishArrayStack and prove a 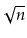 lower-bound like that
in Section 2.6.2. They also present a different structure
that uses a more sophisticated choice of block sizes in order to avoid
computing square roots in the
lower-bound like that
in Section 2.6.2. They also present a different structure
that uses a more sophisticated choice of block sizes in order to avoid
computing square roots in the
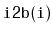 method. With their scheme, the
block containing
method. With their scheme, the
block containing
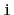 is block
is block
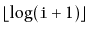 , which is just
the index of the leading 1 bit in the binary representation of
, which is just
the index of the leading 1 bit in the binary representation of
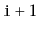 .
Some computer architectures provide an instruction for computing the
index of the leading 1-bit in an integer.
.
Some computer architectures provide an instruction for computing the
index of the leading 1-bit in an integer.
A structure related to the RootishArrayStack is the 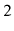 -level
tiered-vector of Goodrich and Kloss [35]. This structure
supports
-level
tiered-vector of Goodrich and Kloss [35]. This structure
supports
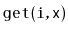 and
and
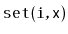 in constant time and
in constant time and
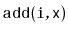 and
and
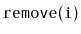 in
in
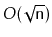 time. These running times are similar
to what can be achieved with the more careful implementation of a
RootishArrayStack discussed in Exercise 2.11.
time. These running times are similar
to what can be achieved with the more careful implementation of a
RootishArrayStack discussed in Exercise 2.11.
Exercise 2..1
In the
ArrayStack implementation, after the first call to
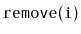
,
the backing array,
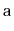
, contains
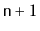
non-
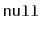
values even
though the
ArrayStack only contains
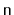
elements. Where is the
extra non-
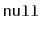
value? Discuss any consequences this might have on
the Java Runtime Environment's memory manager.
Exercise 2..2
The
List method
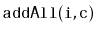
inserts all elements of the
Collection
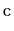
into the list at position
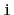
. (The
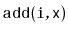
method is a special
case where
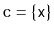
.) Explain why, for the data structures
in this chapter, it is not efficient to implement
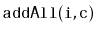
by
repeated calls to
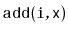
. Design and implement a more efficient
implementation.
Exercise 2..3
Design and implement a
RandomQueue. This is an implementation
of the
Queue interface in which the
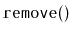
operation removes
an element that is chosen uniformly at random among all the elements
currently in the queue. (Think of a
RandomQueue as a bag in which
we can add elements or reach in and blindly remove some random element.)
The
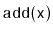
and
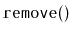
operations in a
RandomQueue should run
in constant time per operation.
Exercise 2..4
Design and implement a
Treque (triple-ended queue). This is a
List
implementation in which
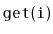
and
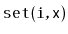
run in constant time
and
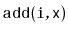
and
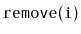
run in time
In other words, modifications are fast if they are near either
end or near the middle of the list.
Exercise 2..5
Implement a method
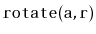
that ``rotates'' the array
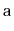
so that
![$ \mathtt{a[i]}$](img179.png)
moves to
![$ \ensuremath{\mathtt{a}}[(\ensuremath{\mathtt{i}}+\ensuremath{\mathtt{r}})\bmod \ensuremath{\mathtt{a.length}}]$](img478.png)
, for all
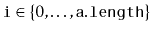
.
Exercise 2..6
Implement a method

that ``rotates'' a
List so that
list item
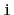
becomes list item
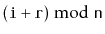
. When run on
an
ArrayDeque, or a
DualArrayDeque,

should run in
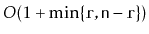
time.
Exercise 2..7
Modify the
ArrayDeque implementation so that the shifting
done by
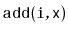
,
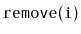
, and
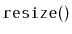
is done using
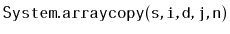
.
Exercise 2..8
Modify the
ArrayDeque implementation so that it does not use the
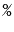
operator (which is expensive on some systems). Instead, it
should make use of the fact that, if
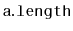
is a power of 2,
then
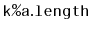
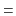
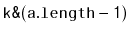
. (Here,
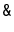
is the bitwise-and
operator.)
Exercise 2..9
Design and implement a variant of
ArrayDeque that does not do any
modular arithmetic at all. Instead, all the data sits in a consecutive
block, in order, inside an array. When the data overruns the beginning
or the end of this array, a modified
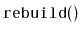
operation is performed.
The amortized cost of all operations should be the same as in an
ArrayDeque.
Hint: Making this work is really all about how a
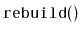 operation is performed. You would like
operation is performed. You would like
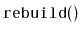 to put the data
structure into a state where the data cannot run off either end until
at least
to put the data
structure into a state where the data cannot run off either end until
at least
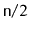 operations have been performed.
operations have been performed.
Test the performance of your implementation against the ArrayDeque.
Optimize your implementation (by using
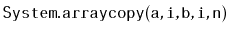 )
and see if you can get it to outperform the ArrayDeque implementation.
)
and see if you can get it to outperform the ArrayDeque implementation.
Exercise 2..10
Design and implement a version of a
RootishArrayStack that has
only
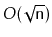
wasted space, but that can perform
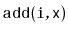
and
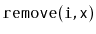
operations in
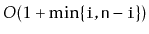
time.
Exercise 2..11
Design and implement a version of a
RootishArrayStack that has
only
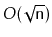
wasted space, but that can perform
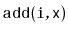
and
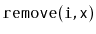
operations in
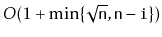
time. (For an idea on how to do this, see Section
3.3.)
Exercise 2..12
Design and implement a version of a
RootishArrayStack that has
only
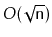
wasted space, but that can perform
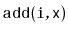
and
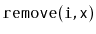
operations in
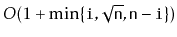
time.
(See Section
3.3 for ideas on how to achieve this.)
Exercise 2..13
Design and implement a
CubishArrayStack. This three level structure
implements the
List interface using at most
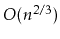
wasted space. In this structure,
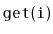
and
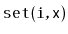
take constant time; while
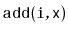
and
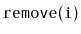
take
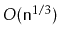
amortized time.
opendatastructures.org
![]() lower-bound like that
in Section 2.6.2. They also present a different structure
that uses a more sophisticated choice of block sizes in order to avoid
computing square roots in the
lower-bound like that
in Section 2.6.2. They also present a different structure
that uses a more sophisticated choice of block sizes in order to avoid
computing square roots in the
![]() method. With their scheme, the
block containing
method. With their scheme, the
block containing
![]() is block
is block
![]() , which is just
the index of the leading 1 bit in the binary representation of
, which is just
the index of the leading 1 bit in the binary representation of
![]() .
Some computer architectures provide an instruction for computing the
index of the leading 1-bit in an integer.
.
Some computer architectures provide an instruction for computing the
index of the leading 1-bit in an integer.
![]() -level
tiered-vector of Goodrich and Kloss [35]. This structure
supports
-level
tiered-vector of Goodrich and Kloss [35]. This structure
supports
![]() and
and
![]() in constant time and
in constant time and
![]() and
and
![]() in
in
![]() time. These running times are similar
to what can be achieved with the more careful implementation of a
RootishArrayStack discussed in Exercise 2.11.
time. These running times are similar
to what can be achieved with the more careful implementation of a
RootishArrayStack discussed in Exercise 2.11.
![]() operation is performed. You would like
operation is performed. You would like
![]() to put the data
structure into a state where the data cannot run off either end until
at least
to put the data
structure into a state where the data cannot run off either end until
at least
![]() operations have been performed.
operations have been performed.
![]() )
and see if you can get it to outperform the ArrayDeque implementation.
)
and see if you can get it to outperform the ArrayDeque implementation.