14.3 Discussion and Exercises

The external memory model of computation was introduced by Aggarwal and Vitter [4]. It is sometimes also called the I/O model or the disk access model.

-Trees are to external memory searching what binary search trees are to internal memory searching.

-trees were introduced by Bayer and McCreight [9] in 1970 and, less than ten years later, they were referred to as ubiquitous in the title of Comer's ACM Computing Surveys article [15].

Like binary search trees, there are many variants of

-Trees including

-trees,

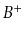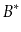-trees, and counted

-trees.

-trees are indeed ubiquitous and are the primary data structure in many file systems, including Apple's HFS+, Microsoft's NTFS, and Linux's Ext4; every major database system; and key-value stores used in cloud computing. Graefe's recent survey [36] provides a 200+ page overview of the many modern applications, variants, and optimizations of

-trees.

-trees implement the SSet interface. If only the USet interface is needed, then external memory hashing could be used as an alternative to

-trees. External memory hashing schemes do exist; see, for example, Reference [43]. These schemes implement the USet operations in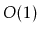

expected time in the external memory model. However, for a variety of reasons, many applications still use

-trees even though they only require USet operations.

One reason

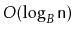-trees are such a popular choice is that they often perform better than their $O(\log_B \ensuremath{\mathtt{n}})$ running time bounds suggest. The reason for this is that, in external memory settings, the value of

is typically quite large--in the hundreds or even thousands. This means that 99% or even 99.9% of the data in a

-tree is stored in the leaves. In a database system with a large memory, it may be possible to cache all the internal nodes of a

-tree in RAM, since they only represent 1% or 0.1% of the total data set. When this happens, this means that a search in a

-tree involves a very fast search in RAM, through the internal nodes, followed by a single external memory access to retrieve a leaf.

Exercise 14..4 The introduction to this chapter claims that

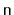
-trees only need an internal memory of size $O(B+\log_B \ensuremath{\mathtt{n}})$ . However, the implementation given here actually requires more memory.

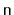
Show that the implementation of the $\mathtt{add(x)}$ and $\mathtt{remove(x)}$ methods given in this chapter use an internal memory proportional to $B\log_B \ensuremath{\mathtt{n}}$ .
Describe how these methods could be modified to reduce their memory consumption to $O(B+\log_B \ensuremath{\mathtt{n}})$ .

Exercise 14..6 Design a modified version of a

-tree in which nodes can have anywhere from

up to

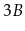
children (and hence

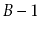
up to

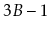
keys). Show that this new version of

-trees performs only

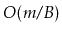
splits, merges, and borrows during a sequence of

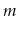
operations. (Hint: For this to work, you will have to be more agressive with merging, sometimes merging two nodes before it is strictly necessary.)

Exercise 14..7 In this exercise, you will design a modified method of splitting and merging in

-trees that asymptotically reduces the number of splits, borrows and merges by considering up to 3 nodes at a time.

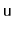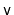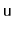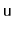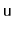Let $\mathtt{u}$ be an overfull node and let $\mathtt{v}$ be a sibling immediately to the right of $\mathtt{u}$ . There are two ways to fix the overflow at $\mathtt{u}$ :
1. $\mathtt{u}$ can give some of its keys to 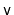$\mathtt{v}$ ; or
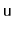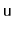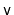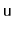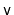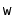2. $\mathtt{u}$ can be split and the keys of $\mathtt{u}$ and $\mathtt{v}$ can be evenly distributed among $\mathtt{u}$ , $\mathtt{v}$ , and the newly created node, $\mathtt{w}$ .
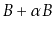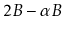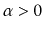Show that this can always be done in such a way that, after the operation, each of the (at most 3) affected nodes has at least $B+\alpha B$ keys and at most $2B-\alpha B$ keys, for some constant $\alpha > 0$ .
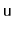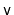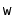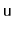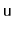Let $\mathtt{u}$ be an underfull node and let $\mathtt{v}$ and $\mathtt{w}$ be siblings of $\mathtt{u}$ There are two ways to fix the underflow at $\mathtt{u}$ :
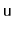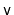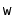1. keys can be redistributed among $\mathtt{u}$ , $\mathtt{v}$ , and $\mathtt{w}$ ; or
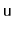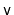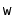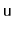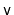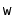2. $\mathtt{u}$ , $\mathtt{v}$ , and $\mathtt{w}$ can be merged into two nodes and the keys of $\mathtt{u}$ , $\mathtt{v}$ , and $\mathtt{w}$ can be redistributed amongst these nodes.
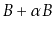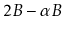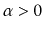Show that this can always be done in such a way that, after the operation, each of the (at most 3) affected nodes has at least $B+\alpha B$ keys and at most $2B-\alpha B$ keys, for some constant $\alpha > 0$ .
Show that, with these modifications, the number of merges, borrows, and splits that occur during 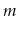operations is .

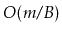Exercise 14..8 A

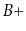
-tree, illustrated in Figure 14.11 stores every key in a leaf and keeps its leaves stored as a doubly-linked list. As usual, each leaf stores between

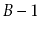
and

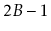
keys. Above this list is a standard

-tree that stores the largest value from each leaf but the last.

Explain how to efficiently implement 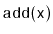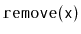$\mathtt{add(x)}$ , $\mathtt{remove(x)}$ , and $\mathtt{find(x)}$ in a 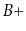-tree.
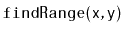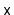Explain how to efficiently implement the $\mathtt{findRange(x,y)}$ method, that reports all values greater than $\mathtt{x}$ and less than or equal to 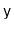$\mathtt{y}$ , in a 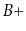-tree.
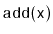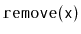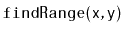Implement a class, BPlusTree, that implements $\mathtt{find(x)}$ , $\mathtt{add(x)}$ , $\mathtt{remove(x)}$ , and $\mathtt{findRange(x,y)}$ .
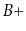-trees duplicate some of the keys because they are stored both in the -tree and in the list. Explain why this duplication does not add up to much for large values of .