Next: 12.2 AdjacencyLists: A Graph Up: 12. Graphs Previous: 12. Graphs Contents
An adjacency matrix is a way of representing an
vertex graph
by an
matrix,
, whose entries are boolean
values.
int n;
boolean[][] a;
AdjacencyMatrix(int n0) {
n = n0;
a = new boolean[n][n];
}
The matrix entry
![$ \mathtt{a[i][j]}$](img1528.png){kind=small}
is defined as
![$\displaystyle \ensuremath{\mathtt{a[i][j]}}=
\begin{cases}
\ensuremath{\math...
...(i,j)}}\in E$} \\
\ensuremath{\mathtt{false}} & \text{otherwise}
\end{cases}$](img1529.png)
With this representation, the
,
, and
operations just
involve setting or reading the matrix entry
:
void addEdge(int i, int j) {
a[i][j] = true;
}
void removeEdge(int i, int j) {
a[i][j] = false;
}
boolean hasEdge(int i, int j) {
return a[i][j];
}
These operations clearly take constant time per operation.
|
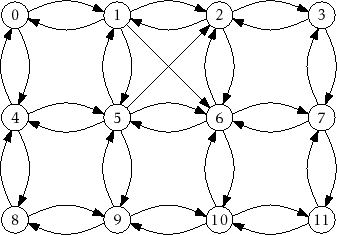
Where the adjacency matrix performs poorly is with the
and
operations. To implement these, we must scan all
entries in the corresponding row or column of
and gather up all the
indices,
, where
, respectively
![$ \mathtt{a[j][i]}$](img1530.png){kind=small}
, is true.
List<Integer> outEdges(int i) {
List<Integer> edges = new ArrayList<Integer>();
for (int j = 0; j < n; j++)
if (a[i][j]) edges.add(j);
return edges;
}
List<Integer> inEdges(int i) {
List<Integer> edges = new ArrayList<Integer>();
for (int j = 0; j < n; j++)
if (a[j][i]) edges.add(j);
return edges;
}
These operations clearly take
time per operation.
Another drawback of the adjacency matrix representation is that it
is big. It stores an
boolean matrix, so it requires at
least
bits of memory. The implementation here uses a matrix
of
values so it actually uses on the
order of
bytes of memory. A more careful implementation, that
packs
boolean values into each word of memory could reduce this
space usage to
words of memory.
,
, and
in constant
time per operation; and
, and
in
time per operation.
.
Despite the high memory usage and poor performance of the
and
operations, an AdjacencyMatrix can still be useful for
some applications. In particular, when the graph 
is dense,
i.e., it has close to
edges, then a memory usage of
may be acceptable.
The AdjacencyMatrix data structure is also commonly used because
algebraic operations on the matrix
can be used to efficiently compute
properties of the graph . This is a topic for a course on algorithms,
but we point out one such property here: If we treat the entries of
as integers (1 for
and 0 for
) and multiply
by itself
using matrix multiplication then we get the matrix
. Recall,
from the definition of matrix multiplication, that
![$\displaystyle \ensuremath{\mathtt{a^2[i][j]}} = \sum_{k=0}^{\ensuremath{\mathtt...
...1} \ensuremath{\mathtt{a[i][k]}}\cdot \ensuremath{\mathtt{a[k][j]}} \enspace .
$](img1535.png)
, this formula counts the
number of vertices,
, such that contains both edges
and
. That is, it counts the number of paths from
to
(through intermediate vertices,
) that have length exactly 2.
This observation is the foundation of an algorithm that computes the
shortest paths between all pairs of vertices in using only
matrix multiplications.
opendatastructures.org