4.5 Discussion and Exercises

Skiplists were introduced by Pugh [50] who also presented a number of applications of skiplists [49]. Since then they have been studied extensively. Several researchers have done very precise analysis of the expected length and variance in length of the search path for the 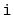$\mathtt{i}$th element in a skiplist [38,37,47]. Deterministic versions [44], biased versions [6,21], and self-adjusting versions [9] of skiplists have all been developed. Skiplist implementations have been written for various languages and frameworks and have seen use in open-source database systems [58,52]. A variant of skiplists is used in the HP-UX operating system kernel's process management structures [36].

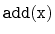
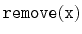
Exercise 4..1   Show that, during an $\mathtt{add(x)}$ or a $\mathtt{remove(x)}$ operation, the expected number of pointers in the structure that get changed is constant.

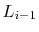
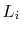
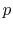
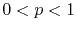
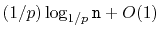
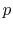
Exercise 4..2   Suppose that, instead of promoting an element from $L_{i-1}$ into $L_i$ based on a coin toss, we promote it with some probability $p$, $0 < p < 1$. Show that the expected length of the search path in this case is at most $(1/p)\log_{1/p} \ensuremath{\mathtt{n}} + O(1)$. What is the value of $p$ that minimizes this expression? What is the expected height of the skiplist? What is the expected number of nodes in the skiplist?

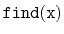
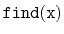
Exercise 4..3   Design and implement a $\mathtt{find(x)}$ method for $\mathtt{SkiplistSSet}$ that avoids locally-redundant comparisons; these are comparisons that have already been done and occur because $\ensuremath{\mathtt{u.next[r]}} = \ensuremath{\mathtt{u.next[r-1]}}$. Analyze the expected number of comparisons done by your modified $\mathtt{find(x)}$ method.

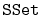
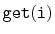
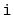
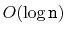
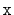
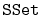
Exercise 4..4   Design and implement a version of a skiplist that implements the $\mathtt{SSet}$ interface, but also allows fast access to elements by rank. That is, it also supports the function $\mathtt{get(i)}$, which returns the element whose rank is $\mathtt{i}$ in $O(\log \ensuremath{\mathtt{n}})$ expected time. 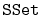(The rank of an element $\mathtt{x}$ in an $\mathtt{SSet}$ is the number of elements in the $\mathtt{SSet}$ that are less than $\mathtt{x}$.)

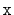
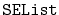
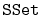
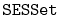
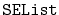
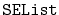
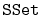
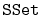
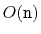
Exercise 4..5   Using the ideas from the space-efficient linked-list, $\mathtt{SEList}$, design and implement a space-efficient $\mathtt{SSet}$, $\mathtt{SESSet}$. Do this by storing the data, in order, in an $\mathtt{SEList}$ and then storing the blocks of this $\mathtt{SEList}$ in an $\mathtt{SSet}$. 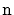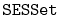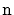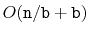If the original $\mathtt{SSet}$ implementation uses $O(\ensuremath{\mathtt{n}})$ space to store $\mathtt{n}$ elements, then the $\mathtt{SESSet}$ will use enough space for $\mathtt{n}$ elements plus $O(\ensuremath{\mathtt{n}}/\ensuremath{\mathtt{b}}+\ensuremath{\mathtt{b}})$ wasted space.

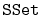
Exercise 4..6   Using an $\mathtt{SSet}$ as your underlying structure, design and implement an application that reads a (large) text file and allow you to search, interactively, for any substring contained in the text.

Hint 1: Every substring is a prefix of some suffix, so it suffices to store all suffixes of the text file.

Hint 2: Any suffix can be represented compactly as a single integer indicating where the suffix begins in the text.

Test your application on some large texts like some of the books available at Project Gutenberg [1].