Next: 6. Binary Trees Up: 5. Hash Tables Previous: 5.3 Hash Codes Contents
Hash tables and hash codes are an enormous and active area of research that is just touched upon in this chapter. The online Bibliography on Hashing [7] contains nearly 2000 entries.
A variety of different hash table implementations exist. The one described in is known as hashing with chaining (each array entry contains a chain (List) of elements). Hashing with chaining dates back to an internal IBM memorandum authored by H. P. Luhn and dated January 1953. This memorandum also seems to be one of the earliest references to linked lists.
An alternative to hashing with chaining is that used by open addressing schemes, where all data is stored directly in an array. These schemes include the LinearHashTable structure of . This idea was also proposed, independently, by a group at IBM in the 1950s. Open addressing schemes must deal with the problem of collision resolution: the case where two values hash to the same array location. Different strategies exist for collision resolution and these provide different performance guarantees and often require more sophisticated hash functions than the ones described here.
Yet another category of hash table implementations are the so-called
perfect hashing methods. These are methods in which
operations take 
time in the worst-case. For static data sets,
this can be accomplished by finding perfect hash functions for
the data; these are functions that map each piece of data to a unique
array location. For data that changes over time, perfect hashing
methods include FKS two-level hash tables [25,19]
and cuckoo hashing [48].
The hash functions presented in this chapter are probably among the most
practical currently known methods that can be proven to work well for any
set of data. Other provably good methods date back to the pioneering work
of Carter and Wegman who introduced the notion of universal hashing
and described several hash functions for different scenarios [11].
Tabulation hashing, described in , is due to Carter
and Wegman [11], but its analysis, when applied to linear probing
(and several other hash table schemes) is due to P
tra
cu and
Thorup [53].
The idea of multiplicative hashing is very old and seems to be
part of the hashing folklore [41, Section 6.4]. However, the
idea of choosing the multiplier
to be a random odd number,
and the analysis in is due to Dietzfelbinger et al. [18]. This version of multiplicative hashing is one of the
simplest, but its collision probability of
is a factor of 2
larger than what one could expect with a random function from
. The multiply-add hashing method uses the function
and
are each randomly chosen from
.
Multiply-add hashing has a collision probability of only
[16], but requires
-bit precision arithmetic.
There are a number of methods of obtaining hash codes from fixed-length
sequences of
-bit integers. One particularly fast method
[8] is the function
is even and
are randomly chosen from
. This yields a
-bit hash code that has
collision probability
. This can be reduced to a
-bit hash
code using multiplicative (or multiply-add) hashing. This method is fast
because it requires only 
-bit multiplications whereas the
method described in requires multiplications.
(The 
operations occur implicitly by using
and
-bit
arithmetic for the additions and multiplications, respectively.)
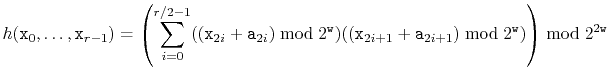
The method from of using polynomials over prime fields
to hash variable-length arrays and strings is due to Dietzfelbinger et al. [17]. It is, unfortunately, not very fast. This is due to its
use of the operator which relies on a costly machine instruction.
Some variants of this method choose the prime
to be one of the form
, in which case the operator can be replaced with
addition (
) and bitwise-and (
) operations [40, Section 3.6].
Another option is to apply one of the fast methods for fixed-length
strings to blocks of length 
for some constant 
and then apply
the prime field method to the resulting sequence of
hash codes.
in Lemma 5.1 is the
best possible by showing that, if
and
,
then
. (Hint look at the binary
representations of
and
and use the fact that
.)
to a LinearHashTable. This code simply stores
in the first
array entry it finds. Explain why this could be
very slow by giving an example of a sequence of
,
, and
operations that would take on the order of
time to execute.
boolean addSlow(T x) {
if (2*(q+1) > t.length) resize(); // max 50% occupancy
int i = hash(x);
while (t[i] != null) {
if (t[i] != del && x.equals(t[i])) return false;
i = (i == t.length-1) ? 0 : i + 1; // increment i (mod t.length)
}
t[i] = x;
n++; q++;
return true;
}
-bit integers
and
. Show why
does not make a good hash code for your object. Give an example of a large set of objects that would all have hash code 0.
-bit integers
and
. Show why
does not make a good hash code for your object.
Give an example of a large set of objects that would all have the same hash code.
-bit integers
and
. Suppose that the hash code for your object is defined by some
deterministic function 
. Prove that there exists a large set
of objects that have the same hash code.
for some positive integer
. Explain why, for a positive integer 
by repeatedly setting
.)