2. Array-Based Lists
In this chapter, we will study implementations of the List and Queue
interfaces where the underlying data is stored in an array, called the
backing array.
The following table summarizes the running times
of operations for the data structures presented in this chapter:
| |
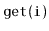 / /
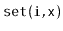 |
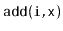 / /
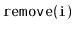 |
| ArrayStack |
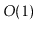 |
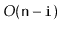 |
| ArrayDeque |
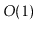 |
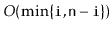 |
| DualArrayDeque |
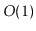 |
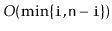 |
| RootishArrayStack |
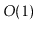 |
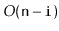 |
Data structures that work by storing data in a single array have many
advantages and limitations in common:
The third point is important. The running times cited in the table
above do not include the cost associated with growing and shrinking
the backing array. We will see that, if carefully managed, the cost of
growing and shrinking the backing array does not add much to the cost of
an average operation. More precisely, if we start with an empty
data structure, and perform any sequence of 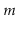
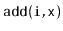 or
or
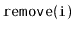 operations, then the total cost of growing and shrinking the backing
array, over the entire sequence of
operations, then the total cost of growing and shrinking the backing
array, over the entire sequence of 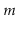 operations is
operations is 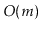 . Although
some individual operations are more expensive, the amortized cost,
when amortized over all
. Although
some individual operations are more expensive, the amortized cost,
when amortized over all 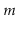 operations, is only
operations, is only 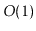 per operation.
per operation.
Subsections
opendatastructures.org