• 8 Scapegoat Trees
• 8.1 ScapegoatTree: A Binary Search Tree with Partial Rebuilding
• 8.1.1 Analysis of Correctness and Running-Time
• 8.1.2 Summary
• 8.2 Discussion and Exercises

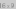
In this chapter, we study a binary search tree data structure, the ScapegoatTree. This structure is based on the common wisdom that, when something goes wrong, the first thing people tend to do is find someone to blame (the scapegoat). Once blame is firmly established, we can leave the scapegoat to fix the problem.

A ScapegoatTree keeps itself balanced by partial rebuilding operations. During a partial rebuilding operation, an entire subtree is deconstructed and rebuilt into a perfectly balanced subtree. There are many ways of rebuilding a subtree rooted at node u into a perfectly balanced tree. One of the simplest is to traverse u's subtree, gathering all its nodes into an array, a, and then to recursively build a balanced subtree using a. If we let \(\texttt{m}=\texttt{a.length}/2\), then the element a[m] becomes the root of the new subtree, \(\texttt{a}[0],\ldots,\texttt{a}[\texttt{m}-1]\) get stored recursively in the left subtree and \(\texttt{a}[\texttt{m}+1],\ldots,\texttt{a}[\texttt{a.length}-1]\) get stored recursively in the right subtree.

    void rebuild(Node<T> u) {
        int ns = size(u);
        Node<T> p = u.parent;
        Node<T>[] a = (Node<T>[]) Array.newInstance(Node.class, ns);
        packIntoArray(u, a, 0);
        if (p == nil) {
            r = buildBalanced(a, 0, ns);
            r.parent = nil;
        } else if (p.right == u) {
            p.right = buildBalanced(a, 0, ns);
            p.right.parent = p;
        } else {
            p.left = buildBalanced(a, 0, ns);
            p.left.parent = p;
        }
    }
    int packIntoArray(Node<T> u, Node<T>[] a, int i) {
        if (u == nil) {
            return i;
        }
        i = packIntoArray(u.left, a, i);
        a[i++] = u;
        return packIntoArray(u.right, a, i);
    }
    Node<T> buildBalanced(Node<T>[] a, int i, int ns) {
        if (ns == 0)
            return nil;
        int m = ns / 2;
        a[i + m].left = buildBalanced(a, i, m);
        if (a[i + m].left != nil)
            a[i + m].left.parent = a[i + m];
        a[i + m].right = buildBalanced(a, i + m + 1, ns - m - 1);
        if (a[i + m].right != nil)
            a[i + m].right.parent = a[i + m];
        return a[i + m];
    }

8.1 ScapegoatTree: A Binary Search Tree with Partial Rebuilding

A ScapegoatTree is a BinarySearchTree that, in addition to keeping track of the number, n, of nodes in the tree also keeps a counter, q, that maintains an upper-bound on the number of nodes.

    int q;

Figure 8.1 A ScapegoatTree with 10 nodes and height 5.

Implementing the find(x) operation in a ScapegoatTree is done using the standard algorithm for searching in a BinarySearchTree (see Section 6.2). This takes time proportional to the height of the tree which, by Equation 8.1 is \(O(\log \texttt{n})\).

To implement the add(x) operation, we first increment n and q and then use the usual algorithm for adding x to a binary search tree; we search for x and then add a new leaf u with \(\texttt{u.x}=\texttt{x}\). At this point, we may get lucky and the depth of u might not exceed \(\log_{3/2}\texttt{q}\). If so, then we leave well enough alone and don't do anything else.

Unfortunately, it will sometimes happen that \(\texttt{depth(u)} > \log_{3/2} \texttt{q}\). In this case, we need to reduce the height. This isn't a big job; there is only one node, namely u, whose depth exceeds \(\log_{3/2} \texttt{q}\). To fix u, we walk from u back up to the root looking for a scapegoat, w. The scapegoat, w, is a very unbalanced node. It has the property that \begin{equation} \frac{\texttt{size(w.child)}}{\texttt{size(w)}} > \frac{2}{3} \enspace , \end{equation} where w.child is the child of w on the path from the root to u. We'll very shortly prove that a scapegoat exists. For now, we can take it for granted. Once we've found the scapegoat w, we completely destroy the subtree rooted at w and rebuild it into a perfectly balanced binary search tree. We know, from Equation 8.2, that, even before the addition of u, w's subtree was not a complete binary tree. Therefore, when we rebuild w, the height decreases by at least 1 so that the height of the ScapegoatTree is once again at most \(\log_{3/2}\texttt{q}\).

    boolean add(T x) {
        // first do basic insertion keeping track of depth
        Node<T> u = newNode(x);
        int d = addWithDepth(u);
        if (d > log32(q)) {
            // depth exceeded, find scapegoat
            Node<T> w = u.parent;
            while (3*size(w) <= 2*size(w.parent))
                w = w.parent;
            rebuild(w.parent);
        }
        return d >= 0;
    }

Figure 8.2 Inserting 3.5 into a ScapegoatTree increases its height to 6, which violates Equation 8.1 since \(6 > \log_{3/2} 11 \approx 5.914\). A scapegoat is found at the node containing 5.

The implementation of remove(x) in a ScapegoatTree is very simple. We search for x and remove it using the usual algorithm for removing a node from a BinarySearchTree. (Note that this can never increase the height of the tree.) Next, we decrement n, but leave q unchanged. Finally, we check if \(\texttt{q} > 2\texttt{n}\) and, if so, then we rebuild the entire tree into a perfectly balanced binary search tree and set \(\texttt{q}=\texttt{n}\).

    boolean remove(T x) {
        if (super.remove(x)) {
            if (2*n < q) {
                rebuild(r);
                q = n;
            }
            return true;
        }
        return false;
    }

8.1.1 Analysis of Correctness and Running-Time

In this section, we analyze the correctness and amortized running time of operations on a ScapegoatTree. We first prove the correctness by showing that, when the add(x) operation results in a node that violates Condition Equation 8.1, then we can always find a scapegoat:

Next, we analyze the parts of the running time that are not yet accounted for. There are two parts: The cost of calls to size(u) when searching for scapegoat nodes, and the cost of calls to rebuild(w) when we find a scapegoat w. The cost of calls to size(u) can be related to the cost of calls to rebuild(w), as follows:

All that remains is to prove an upper-bound on the cost of all calls to rebuild(u) during a sequence of \(m\) operations:

8.1.2 Summary

8.2 Discussion and Exercises

The term scapegoat tree is due to Galperin and Rivest [33], who define and analyze these trees. However, the same structure was discovered earlier by Andersson [5,7], who called them general balanced trees since they can have any shape as long as their height is small.

Experimenting with the ScapegoatTree implementation will reveal that it is often considerably slower than the other SSet implementations in this book. This may be somewhat surprising, since height bound of \begin{equation*} \log_{3/2}\texttt{q} \approx 1.709\log \texttt{n} + O(1) \end{equation*} is better than the expected length of a search path in a Skiplist and not too far from that of a Treap. The implementation could be optimized by storing the sizes of subtrees explicitly at each node or by reusing already computed subtree sizes (Exercises Exercise 8.5 and Exercise 8.6). Even with these optimizations, there will always be sequences of add(x) and delete(x) operation for which a ScapegoatTree takes longer than other SSet implementations.

This gap in performance is due to the fact that, unlike the other SSet implementations discussed in this book, a ScapegoatTree can spend a lot of time restructuring itself. Exercise 8.3 asks you to prove that there are sequences of n operations in which a ScapegoatTree will spend on the order of \(\texttt{n}\log \texttt{n}\) time in calls to rebuild(u). This is in contrast to other SSet implementations discussed in this book, which only make \(O(\texttt{n})\) structural changes during a sequence of n operations. This is, unfortunately, a necessary consequence of the fact that a ScapegoatTree does all its restructuring by calls to rebuild(u) [20].

Despite their lack of performance, there are applications in which a ScapegoatTree could be the right choice. This would occur any time there is additional data associated with nodes that cannot be updated in constant time when a rotation is performed, but that can be updated during a rebuild(u) operation. In such cases, the ScapegoatTree and related structures based on partial rebuilding may work. An example of such an application is outlined in Exercise 8.11.