1.8 Discussion and Exercises

The List, USet, and SSet interfaces described in Section 1.2 are influenced by the Java Collections Framework [54]. These are essentially simplified versions of the List, Set, Map, SortedSet, and SortedMap interfaces found in the Java Collections Framework.

For a superb (and free) treatment of the mathematics discussed in this chapter, including asymptotic notation, logarithms, factorials, Stirling's approximation, basic probability, and lots more, see the textbook by Leyman, Leighton, and Meyer [50]. For a gentle calculus text that includes formal definitions of exponentials and logarithms, see the (freely available) classic text by Thompson [71].

For more information on basic probability, especially as it relates to computer science, see the textbook by Ross [63]. Another good reference, which covers both asymptotic notation and probability, is the textbook by Graham, Knuth, and Patashnik [37].

Exercise 1..1   This exercise is designed to help familiarize the reader with choosing the right data structure for the right problem. If implemented, the parts of this exercise should be done by making use of an implementation of the relevant interface (Stack, Queue, Deque, USet, or SSet) provided by the .

Solve the following problems by reading a text file one line at a time and performing operations on each line in the appropriate data structure(s). Your implementations should be fast enough that even files containing a million lines can be processed in a few seconds.

1. Read the input one line at a time and then write the lines out in reverse order, so that the last input line is printed first, then the second last input line, and so on.

2. Read the first 50 lines of input and then write them out in reverse order. Read the next 50 lines and then write them out in reverse order. Do this until there are no more lines left to read, at which point any remaining lines should be output in reverse order.

   In other words, your output will start with the 50th line, then the 49th, then the 48th, and so on down to the first line. This will be followed by the 100th line, followed by the 99th, and so on down to the 51st line. And so on.

   Your code should never have to store more than 50 lines at any given time.

3. Read the input one line at a time. At any point after reading the first 42 lines, if some line is blank (i.e., a string of length 0), then output the line that occured 42 lines prior to that one. For example, if Line 242 is blank, then your program should output line 200. This program should be implemented so that it never stores more than 43 lines of the input at any given time.

4. Read the input one line at a time and write each line to the output if it is not a duplicate of some previous input line. Take special care so that a file with a lot of duplicate lines does not use more memory than what is required for the number of unique lines.

5. Read the input one line at a time and write each line to the output only if you have already read this line before. (The end result is that you remove the first occurrence of each line.) Take special care so that a file with a lot of duplicate lines does not use more memory than what is required for the number of unique lines.

6. Read the entire input one line at a time. Then output all lines sorted by length, with the shortest lines first. In the case where two lines have the same length, resolve their order using the usual ``sorted order.'' Duplicate lines should be printed only once.

7. Do the same as the previous question except that duplicate lines should be printed the same number of times that they appear in the input.

8. Read the entire input one line at a time and then output the even numbered lines (starting with the first line, line 0) followed by the odd-numbered lines.

9. Read the entire input one line at a time and randomly permute the lines before outputting them. To be clear: You should not modify the contents of any line. Instead, the same collection of lines should be printed, but in a random order.

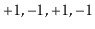
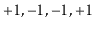
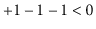
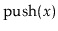
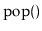
Exercise 1..2   A Dyck word is a sequence of +1's and -1's with the property that the sum of any prefix of the sequence is never negative. For example, $+1,-1,+1,-1$ is a Dyck word, but $+1,-1,-1,+1$ is not a Dyck word since the prefix $+1-1-1<0$. Describe any relationship between Dyck words and Stack $\ensuremath{\mathrm{push}(\ensuremath{\mathit{x}})}$ and $\ensuremath{\mathrm{pop}()}$ operations.

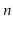
Exercise 1..3   A matched string is a sequence of {, }, (, ), [, and ] characters that are properly matched. For example, ``{{()[]}}'' is a matched string, but this ``{{()]}'' is not, since the second { is matched with a ]. 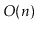Show how to use a stack so that, given a string of length $\ensuremath{\ensuremath{\mathit{n}}}$, you can determine if it is a matched string in $O(\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}})$ time.

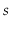
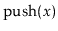
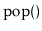
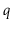
Exercise 1..4   Suppose you have a Stack, $\ensuremath{\ensuremath{\mathit{s}}}$, that supports only the $\ensuremath{\mathrm{push}(\ensuremath{\mathit{x}})}$ and $\ensuremath{\mathrm{pop}()}$ operations. Show how, using only a FIFO Queue, $\ensuremath{\ensuremath{\mathit{q}}}$, you can reverse the order of all elements in $\ensuremath{\ensuremath{\mathit{s}}}$.

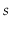
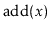
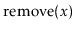
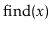
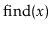
Exercise 1..5   Using a USet, implement a Bag. A Bag is like a USet--it supports the $\ensuremath{\mathrm{add}(\ensuremath{\mathit{x}})}$, $\ensuremath{\mathrm{remove}(\ensuremath{\mathit{x}})}$ and $\ensuremath{\mathrm{find}(\ensuremath{\mathit{x}})}$ methods--but it allows duplicate elements to be stored. The $\ensuremath{\mathrm{find}(\ensuremath{\mathit{x}})}$ operation in a Bag returns some element (if any) that is equal to $\ensuremath{\ensuremath{\mathit{x}}}$. 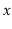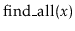In addition, a Bag supports the $\ensuremath{\mathrm{find\_all}(\ensuremath{\mathit{x}})}$ operation that returns a list of all elements in the Bag that are equal to $\ensuremath{\ensuremath{\mathit{x}}}$.

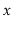
Exercise 1..6   From scratch, write and test implementations of the List, USet and SSet interfaces. These do not have to be efficient. They can be used later to test the correctness and performance of more efficient implementations. (The easiest way to do this is to store the elements in an array.)

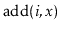
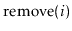
Exercise 1..7   Work to improve the performance of your implementations from the previous question using any tricks you can think of. Experiment and think about how you could improve the performance of $\ensuremath{\mathrm{add}(\ensuremath{\mathit{i}},\ensuremath{\mathit{x}})}$ and $\ensuremath{\mathrm{remove}(\ensuremath{\mathit{i}})}$ in your List implementation. 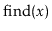Think about how you could improve the performance of the $\ensuremath{\mathrm{find}(\ensuremath{\mathit{x}})}$ operation in your USet and SSet implementations. This exercise is designed to give you a feel for how difficult it can be to obtain efficient implementations of these interfaces.