12.1 AdjacencyMatrix: Representing a Graph by a Matrix

An adjacency matrix is a way of representing an $\ensuremath{\ensuremath{\mathit{n}}}$ vertex graph $G=(V,E)$ by an $\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}\times\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}$ matrix, $\ensuremath{\ensuremath{\mathit{a}}}$, whose entries are boolean values.

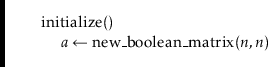
The matrix entry $\ensuremath{\ensuremath{\mathit{a}}[\ensuremath{\mathit{i}}]}[\ensuremath{j}]$ is defined as

$$\ensuremath{\ensuremath{\ensuremath{\mathit{a}}[\ensuremath{\math... ...emath{\ensuremath{\ensuremath{\mathit{false}}}} & \text{otherwise} \end{cases}$$

The adjacency matrix for the graph in Figure 12.1 is shown in Figure 12.2.

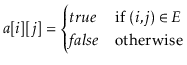
In this representation, the operations $\ensuremath{\mathrm{add\_edge}(\ensuremath{\mathit{i}},\ensuremath{\mathit{j}})}$, $\ensuremath{\mathrm{remove\_edge}(\ensuremath{\mathit{i}},\ensuremath{\mathit{j}})}$, and $\ensuremath{\mathrm{has\_edge}(\ensuremath{\mathit{i}},\ensuremath{\mathit{j}})}$ just involve setting or reading the matrix entry $\ensuremath{\ensuremath{\mathit{a}}[\ensuremath{\mathit{i}}]}[\ensuremath{j}]$:

These operations clearly take constant time per operation.

Figure 12.2: A graph and its adjacency matrix.

	0	1	2	3	4	5	6	7	8	9	10	11
0	0	1	0	0	1	0	0	0	0	0	0	0
1	1	0	1	0	0	1	1	0	0	0	0	0
2	1	0	0	1	0	0	1	0	0	0	0	0
3	0	0	1	0	0	0	0	1	0	0	0	0
4	1	0	0	0	0	1	0	0	1	0	0	0
5	0	1	1	0	1	0	1	0	0	1	0	0
6	0	0	1	0	0	1	0	1	0	0	1	0
7	0	0	0	1	0	0	1	0	0	0	0	1
8	0	0	0	0	1	0	0	0	0	1	0	0
9	0	0	0	0	0	1	0	0	1	0	1	0
10	0	0	0	0	0	0	1	0	0	1	0	1
11	0	0	0	0	0	0	0	1	0	0	1	0

Where the adjacency matrix performs poorly is with the $\ensuremath{\mathrm{out\_edges}(\ensuremath{\mathit{i}})}$ and $\ensuremath{\mathrm{in\_edges}(\ensuremath{\mathit{i}})}$ operations. To implement these, we must scan all $\ensuremath{\ensuremath{\mathit{n}}}$ entries in the corresponding row or column of $\ensuremath{\ensuremath{\mathit{a}}}$ and gather up all the indices, $\ensuremath{\ensuremath{\mathit{j}}}$, where $\ensuremath{\ensuremath{\mathit{a}}[\ensuremath{\mathit{i}}]}[\ensuremath{j}]$, respectively $\ensuremath{\ensuremath{\mathit{a}}[\ensuremath{\mathit{j}}]}[\ensuremath{i}]$, is true. These operations clearly take $O(\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}})$ time per operation.

Another drawback of the adjacency matrix representation is that it is large. It stores an $\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}\times \ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}$ boolean matrix, so it requires at least $\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}^2$ bits of memory. The implementation here uses a matrix of values so it actually uses on the order of $\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}^2$ bytes of memory. A more careful implementation, which packs $\ensuremath{\ensuremath{\mathit{w}}}$ boolean values into each word of memory, could reduce this space usage to $O(\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}^2/\ensuremath{\ensuremath{\ensuremath{\mathit{w}}}})$ words of memory.

Theorem 12..1   The AdjacencyMatrix data structure implements the Graph interface. An AdjacencyMatrix supports the operations

• $\ensuremath{\mathrm{add\_edge}(\ensuremath{\mathit{i}},\ensuremath{\mathit{j}})}$, $\ensuremath{\mathrm{remove\_edge}(\ensuremath{\mathit{i}},\ensuremath{\mathit{j}})}$, and $\ensuremath{\mathrm{has\_edge}(\ensuremath{\mathit{i}},\ensuremath{\mathit{j}})}$ in constant time per operation; and
• $\ensuremath{\mathrm{in\_edges}(\ensuremath{\mathit{i}})}$, and $\ensuremath{\mathrm{out\_edges}(\ensuremath{\mathit{i}})}$ in $O(\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}})$ time per operation.

The space used by an AdjacencyMatrix is $O(\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}^2)$.

Despite its high memory requirements and poor performance of the $\ensuremath{\mathrm{in\_edges}(\ensuremath{\mathit{i}})}$ and $\ensuremath{\mathrm{out\_edges}(\ensuremath{\mathit{i}})}$ operations, an AdjacencyMatrix can still be useful for some applications. In particular, when the graph $G$ is dense, i.e., it has close to $\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}^2$ edges, then a memory usage of $\ensuremath{\ensuremath{\ensuremath{\mathit{n}}}}^2$ may be acceptable.

The AdjacencyMatrix data structure is also commonly used because algebraic operations on the matrix $\ensuremath{\ensuremath{\mathit{a}}}$ can be used to efficiently compute properties of the graph $G$. This is a topic for a course on algorithms, but we point out one such property here: If we treat the entries of $\ensuremath{\ensuremath{\mathit{a}}}$ as integers (1 for $\ensuremath{\ensuremath{\mathit{true}}}$ and 0 for $\ensuremath{\ensuremath{\mathit{false}}}$) and multiply $\ensuremath{\ensuremath{\mathit{a}}}$ by itself using matrix multiplication then we get the matrix $\ensuremath{\ensuremath{\ensuremath{\mathit{a}}}}^2$. Recall, from the definition of matrix multiplication, that

$$\ensuremath{\ensuremath{\ensuremath{\mathit{a}}\ensuremath{\oplus... ...{\ensuremath{\mathit{a}}[\ensuremath{\mathit{k}}]}[\ensuremath{j}]} \enspace .$$

Interpreting this sum in terms of the graph $G$, this formula counts the number of vertices, $\ensuremath{\ensuremath{\ensuremath{\mathit{k}}}}$, such that $G$ contains both edges $\ensuremath{(\ensuremath{\mathit{i}},\ensuremath{\mathit{k}})}$ and $\ensuremath{(\ensuremath{\mathit{k}},\ensuremath{\mathit{j}})}$. That is, it counts the number of paths from $\ensuremath{\ensuremath{\ensuremath{\mathit{i}}}}$ to $\ensuremath{\ensuremath{\ensuremath{\mathit{j}}}}$ (through intermediate vertices, $\ensuremath{\ensuremath{\ensuremath{\mathit{k}}}}$) whose length is exactly two. This observation is the foundation of an algorithm that computes the shortest paths between all pairs of vertices in $G$ using only $O(\log \ensuremath{\ensuremath{\ensuremath{\mathit{n}}}})$ matrix multiplications.